Mathématiques, DNB Nlle Calédonie 2022.

Exercice 1 : Vrai ou Faux 18 points
Pour chacune des trois affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant la réponse.
Affirmation n° 1 : La vitesse d’un avion qui vole à 1200 km/h est supérieure à la vitesse du son qui est 340,29 m/s. Faux.
1200 / 3,6 ~333 m /s.
Affirmation n° 2 : Pour tout nombre x, on a 4(4x −4)+16 = 16x². Faux.
4(4x −4)+16 = 16 x-16 +16 = 16 x.
Affirmation n° 3 : 33×13 est la décomposition en produit de facteurs premiers de 429. Faux.
429 = 3 x 11 x13. ( 33 n'est pas un nombre premier ).

Exercice 2 : QCM 12 points
Cet exercice est un questionnaire à choix multiples (QCM).
Pour chaque question, une seule des trois réponses proposées est exacte.
Sur la copie, indiquer le numéro de la question et la réponse A, B ou C choisie.
Aucune justification n’est demandée.
Aucun point ne sera enlevé en cas demauvaise réponse.
1. Dans un tableur, quelle formule faut-il saisir dans la cellule D1 pour afficher la somme des nombres des cellules A1, B1 et C1?

	A	B	C	D
1	3	5	4

= somme ( A1:C1) réponse A.

2. Soit la série de nombres :
15; 10; 13; 9; 10; x.
La moyenne de la série est 11 pour x égal à . . .
(15 +10 +13 +9 +10 +x) / 6 = 11 ; 57 +x = 66 ; x = 9. réponse A.

3. Sur la Terre, l’équateur est : un parallèle. réponse C.

4. Le volume exact, en cm³, d’une boule de 6 cm de diamètre est :
4 / 3 p R³ = 4 / 3 p x3³ =36 p. réponse A.

Exercice 3 : Le vent 12 points
On a relevé la vitesse du vent à 13 heures du 1er au 15 novembre sur une plage de Nouvelle- Calédonie.
Les vitesses approchées sont données, en noeuds, dans le tableau ci-dessous :

jour	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
vitesse	10	15	20	20	15	10	10	20	15	25	25	25	20	15	15

1. À partir des données ci-dessus, compléter le tableau suivant :

vitesse	10	15	20	25
nombre de jours	3	5	4	3
Fréquence en %	3 / 15 x100=20	5 / 15 x100 ~ 33	4 / 15 x100~ 27	3 / 15 x100=20

2. Calculer le pourcentage de jours où la vitesse de vent est supérieure ou égale à 15 noeuds sur la plage.
33+27+20= 80 %.
3. Déterminer la vitesse médiane du vent sur la plage durant cette période.
10 ; 10 ; 10 ; 15 ; 15 ; 15 ; 15 ; 15 ; 20 ; 20 ; 20 ; 20 ; 25 ; 25 ; 25.
La vitesse médiane est 15 noeuds.

Exercice 4 : Construction 20 points
Un triangle MWB est tel que MB = 7,5 cm ; WB = 4,5 cm et MW= 6 cm.
1. Construire le triangle MWB.
2. Montrer que le triangle MWB est rectangle en W.
WB² +WM² = 4,5² + 6² = 56,25.
MB² = 7,5² =56,25.
WB² +WM² = MB² ; d'après la réciproque du théorème de Pythagore, ce triangle est rectangle en W.
3. Calculer la mesure de l’angleƒ BMW. Arrondir le résultat au degré près.
tan ( BMW) =BW / MW = 4,5 / 6 =0,75 ; cet angle mesure 37 °.
4. a. Placer le point F sur le segment [WB] tel que WF = 3 cm.
b. Tracer la parallèle à (MB) passant par F. Elle coupe (MW) en E. Placer le point E.
c. Calculer WE.
Relation de Thalès :

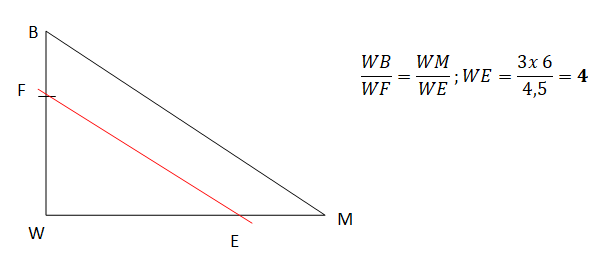5. a. Placer le point T sur la demi-droite [MW) de la figure précédente tel que MT = 10 cm.
b. Tracer le segment [TB].
6. Calculer la longueur TE.

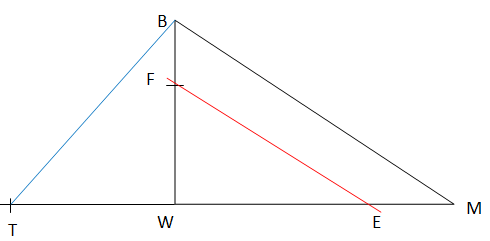
TE = TM -EM avec Em = 6,5 -4 = 2,5 cm.
TE = 10-2,5 = 7,5 cm.

Exercice 5 : Le club 20 points
Juliette désire apprendre la planche à voile, elle prend des renseignements auprès d’un club qui propose trois tarifs mensuels.
• Le tarif découverte à 1 600 F par heure de cours.
• Le tarif personnalisé qui comprend une carte d’adhérent à 4 800 F et un prix fixe de 600 F par heure de cours.
• Le tarif renforcé à 9 600 F pour un nombre illimité d’heures de cours.

1. Calculer le prix à payer pour 4 heures de cours avec le tarif découverte.
4 x1600 = 6400 F.
2. a. Montrer que 4 heures de cours avec le tarif personnalisé coûtent 7200 F.
4800 + 4 x 600 =7200 F.
b. Calculer le prix à payer pour 10 heures de cours avec le tarif personnalisé.
4800 + 10 x 600 = 10 800 F.
On désigne par x le nombre d’heures de cours. On note P(x) le prix à payer en francs avec le tarif personnalisé.
c. Exprimer P(x) en fonction de x.
P(x) = 4800 + 600 x.
Les fonctions donnant les prix à payer avec les tarifs découverte et renforcé sont représentées ci dessous.
3. a. Pour combien d’heures de cours ces deux tarifs sont-ils égaux ?
6 heures.
b. Tracer la représentation graphique de la fonction P définie par P(x) = 600x +4800.

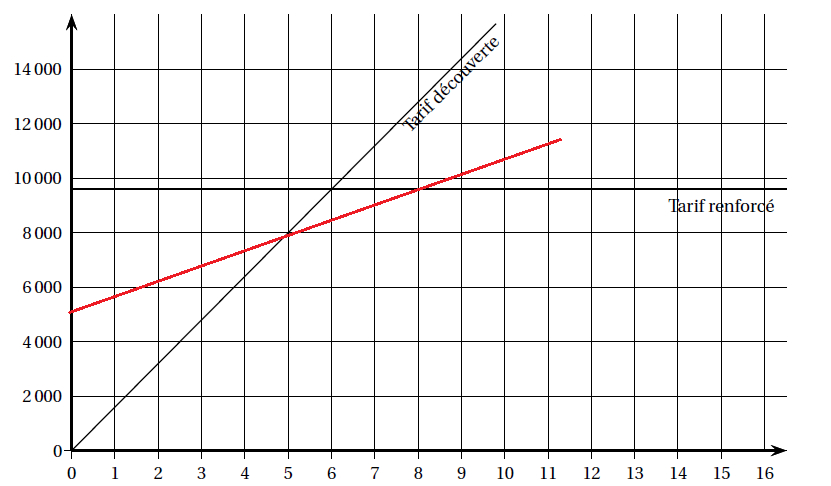
c. Quel est le tarif le plus économique pour Juliette si elle décide de prendre 7 heures de cours ?
Justifier la réponse.
Tarif renforcé : 9 600 F.
Tarif découverte : 1600 x 7 =11 200 F.
Tarif personnalisé : 4800 + 7 x600 =9 000 F.
4. Pour combien d’heures de cours Juliette paie-t-elle le même prix avec le tarif personnalisé et le tarif renforcé ?
9600 = 4800 +600 x ; x = 8.