Mathématiques, DNB Nlle Calédonie 2021. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Exercice 1 : Vrai ou Faux 18 points Pour chaque affirmation répondre par vrai ou faux. Justifier chaque réponse. Affirmation 1 : 50% de 10 350 c’est 10 300. Faux. 10 350 x 0,50=5 175. Affirmation 2 : 7  / 3 est la forme irréductible de 42 / 18. Vrai. 42 = 2 x3 x7 ; 18 = 2 x3 x3. 42 / 18 = 7 / 3. Affirmation 3 : L’équation 2x −4 = −x +5 a pour solution 3. Vrai. 2x+x=5+4 ; 3x = 9  ; x = 3. Affirmation 4 : L’arrondi à l’unité près du volume d’une boule de diamètre 21,6 cm est 42 213 cm3. Faux. On rappelle la formule du volume d’une boule V =4 / 3 p R3 = 4 / 3 x3,14 x10,83 ~ 5277 cm3. Affirmation 5 : Dans la figure codée ci-dessous, la mesure de l’angle� DNB, arrondie à l’unité près, est 18°. Vrai. 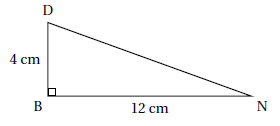tan (DNB) = BD / BN = 4 / 12 ~0,333 ; angle (DNB) ~18°. Affirmation 6 : On peut composer 6 codes différents avec un cadenas à 3 chiffres qui respecte les conditions suivantes : • les deux premiers chiffres sont choisis parmi 1; 2 et 3; • un chiffre peut apparaître deux fois ; • le dernier chiffre est 6. (1 ; 1 ; 6) ; (1 ; 2 ; 6) ; (1 ; 3 ; 6) ; (2 ; 1 ; 6) ; (2 ; 2 ; 6) ; (2 ; 3 ; 6) ; ( 3 ; 1 ; 6) ; (3 ; 2 ; 6)  ; (3 ; 3 ; 6). Faux. Exercice 2 : 10 points On étudie les précipitations (hauteurs de pluies) sur la ville de Nouméa entre avril et décembre 2020. On obtient le tableau suivant : Mois avril mai juin juillet août septembre octobre novembre décembre Précipitations (mm) 147 199 40 67 47 54 104 45 63 1. Calculer la moyenne des précipitations. Arrondir le résultat au mm près. (147 +199 +40 +67 +47 +54 +104 +45 +63) / 9 ~ 85 mm. 2. Quelle est l’étendue des précipitations ? 199 -40=159 mm. 3. Déterminer la médiane des précipitations. La médiane partage la série en deux parties égales. 40 ; 45 ; 47 ; 54 ; 63 ; 67 ; 104 ; 147 ; 199. 4. Calculer le pourcentage de mois pour lesquels les précipitations sont supérieures à 100 mm. Arrondir le résultat à l’unité près. 3 mois sur 9 soit 3 / 9 x100 ~ 33 %. Exercice 3 : 10 points BAI est un triangle rectangle en A tel que BA = 210 cm et AI = 155 cm. 1. Déterminer la longueur BI au cm près. Relation de Pythagore. BI2 = BA2 + AI2 =2102 + 1552 =68 125 ; BI = racine carrée (68 125) ~ 261 cm. L’immeuble de Joanne possède 15 vitres rectangulaires. Chaque vitre a pour longueur 210 cm et pour largeur 155 cm. Lors d’une préalerte cyclonique Joanne pose de l’adhésif sur les deux diagonales de chaque vitre de l’immeuble. Une bande d’adhésif est assimilée à une diagonale du rectangle 2. Justifier que Joanne a besoin d’environ 5,22 m d’adhésif pour une vitre. Pour une vitre : 2 x2,61 = 5,22 m. Joanne a 7 rouleaux d’adhésif de 10 m chacun. 3. A-t-elle assez d’adhésif pour toutes les vitres ? Justifier la réponse. Pour 15 vitres : 15 x 5,22 ~78,3 m. Cette valeur étant supérieure à 70 m, c'est insuffisant. Exercice 4 : 14 points 1. a. Justifier que 330 n’est pas un nombre premier. 330 est pair, il est divisible par 1 ; 2 ; 3 ; 5 ; 10 ; 11 ; .....330), donc il n'est pas premier. La décomposition en produit de facteurs premiers de 500 est : 500 = 22 ×53. b. Décomposer 330 en produit de facteurs premiers. 330 = 2 x 3 x 5 x11. c. Justifier que 165 divise 330. 165 = 3 x 5 x11 ; 165  x 2 = 330. d. Justifier que 165 ne divise pas 500. 500 / 165 = 2 x25 / (3 x11) diffère d'un nombre entier. La pâtisserie Délices a préparé 330 biscuits aux noix et 500 biscuits au chocolat. La pâtisserie souhaite répartir le plus de biscuits possible dans 165 boites. La pâtisserie met le même nombre de biscuits aux noix dans chaque boîte. 2. Combien de biscuits aux noix y a-t-il dans chaque boîte? 330 / 165 = 2. La pâtisserie met aussi le même nombre de biscuits au chocolat dans chaque boîte. 3. a. Combien de biscuits au chocolat y a-t-il dans chaque boîte? 500 =165 x 3 +5. Donc 3 biscuits au chocolat par boîte. b. Combien de biscuits au chocolat reste-t-il ? Il reste 5 biscuits au chocolat. Une boîte de biscuits coûte 3 650 francs. À partir de 10 boîtes achetées, la pâtisserie Délices offre une réduction de 5% sur le montant total. 4. Combien va-t-on payer pour l’achat de 12 boîtes ? Faire apparaÎtre les calculs effectués. 3650 x 12 = 43 800 F. Remise :43 800 x 10 /100 = 4380 F. Prix payé : 43 800 -4380 = 39 420 F. ... .... Exercice 5 : 18 points Un jeu est constitué de quatre familles de cartes : banane; prune; citron; fraise. Voici la répartition des cartes de la famille banane. Nombre de banane(s) 1 2 3 4 5 Nombre de cartes 5 3 3 2 1 La répartition est la même pour les cartes avec les autres fruits. 1. Montrer que ce jeu a 56 cartes. 14 x 4 =56. Joanne mélange toutes les cartes. Son frère Jack prend une carte au hasard. On admet que chaque carte a la même chance d’être choisie. Soit P l’évènement : « Jack obtient une carte de la famille prune ». 2. Quelle est la probabilité de l’évènement P ? 14 carte dans la famille prune sur 56 cartes. Probabilité de tirer une carte de la famille prune = 14 / 56 = 0,25. 3. a. Quel est l’évènement contraire de P ? Tirer une carte qui n'appartient pas à la famille prune. b. Quelle est la probabilité de l’évènement contraire de P ? 1 -0,25 = 0,75. 4. Quelle est la probabilité d’obtenir une carte avec quatre fruits ? 2 cartes possède 4 fruits dans chaque famille soit 8 cartes. probabilité d'obtenir une carte avec 4 fruits : 8 / 56 = 1 / 7 ~ 0,14. Exercice 6 : 14 points Les parties 1 et 2 sont indépendantes Partie 1 : Distance de réaction La distance de réaction d’un véhicule est la distance parcourue par ce véhicule entre l’instant où le conducteur voit un obstacle et l’instant où il appuie sur la pédale de frein. On considère un conducteur en bonne santé. La distance de réaction, en mètre, en fonction de la vitesse du véhicule est représentée par le graphique suivant. 1. Cette représentation graphique traduit-elle une situation de proportionnalité? Justifier la réponse. Oui, le graphe est une droite passant par l'origine. 2. Compléter, par lecture graphique, le tableau suivant. vitesse ( km / h) 0 54 90 distance de réaction (m) 0 15 25 Partie 2 : Distance de freinage sur route sèche La distance de freinage d’un véhicule est la distance parcourue par ce véhicule entre l’instant où le conducteur appuie sur la pédale de frein et l’instant où la voiture s’arrête complètement. La distance de freinage en mètre, pour un véhicule en bon état, est déterminée en fonction de la vitesse du véhicule par la formule : d =v2 / 203,2 où v est la vitesse exprimée en km/h. On utilise un tableur pour calculer les distances de freinage en fonction de la vitesse : A B C D 1 vitesse ( km / h) 10 20 30 2 distance de freinage (m) 1. Recopier parmi les formules trois suivantes, celle qu’il faut saisir dans la cellule B2 puis étirer vers la droite : = 2*B1/203.2  ; = B1*B1/203.2 ; = B1+B1/203.2 2. Un véhicule roule à 90 km/h. Montrer que sa distance de freinage est environ 40 m. d = 902 / 203,4 ~40 m. Partie 3 : Distance d’arrêt sur route sèche La distance d’arrêt d’un véhicule est la distance parcourue par ce véhicule entre l’instant où le conducteur voit un obstacle et l’instant où la voiture s’arrête complètement. Distance d’arrêt = Distance de réaction + Distance de freinage Calculer la distance d’arrêt d’un véhicule roulant à 90 km/h. 25 +40 = 65 m. Exercice 7 : 9 points On doit appliquer deux couches de peinture sur le sol et les parois intérieures d’une piscine rectangulaire dont les dimensions  : longueur = 8 m, largeur = 4 m, profondeur =1,70 m. Calculer le budget que l’on doit prévoir pour les travaux de peinture. Surface à couvrir : 2 (longueur + largeur) x hauteur=2(8+4) x1,70 =40,8 m2. Pour deux couches : 81,6 m2. Un pot de peinture couvre 35 m2, il faut donc pots. Prix : 12 000 x3 = 36 000 F. Exercice 8 : 13 points On dispose des informations suivantes sur le phare Amédée, une balise et une bouée : — la hauteur du phare est de 56 m; — la balise est située à 260 m du phare; — la balise et la bouée sont distantes de 151 m; — la bouée O, le sommet B de la balise et le sommet P du phare sont considérés comme trois points alignés. Schéma de la situation : Les droites (PH) et (BA) sont parallèles. 1. Quelle est la distance OH en m ? OH = 260 +151 =411 m. 2. Déterminer la hauteur AB de la balise. Arrondir au dixième de m près. Rédiger la réponse en faisant apparaître les différentes étapes. Relation de Thalès : AB / PH = OA / OH. AB = OA x PH / OH = 151 x56 / 411 ~20,6 m. Le haut du phare est protégé par une barrière composée de sculptures. On souhaite réaliser un programme Scratch pour reproduire le contour de cette sculpture. 3. Calculer la mesure de l’angle "a" en degré dans la figure ci-dessus : 180 -72 =108°. Le script 1 permet de tracer le motif en pointillé ci-dessous (on part du point A et on s’arrête au point B). 4. Compléter le script 1. Le script final permet de réaliser le contour de la sculpture. 5. Compléter le script final.

menu