La pente d'eau de Montech, bac Amérique du Nord 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... La pente d’eau de Montech est un ascenseur à bateaux établi sur un canal latéral de la Garonne. Un panneau vertical en acier appelé masque retient l’eau sur laquelle le bateau flotte. Deux automotrices, liées entre elles, poussent le système {bateau + eau + masque} par l’intermédiaire de deux bras. A. Étude cinématique du mouvement du système {bateau + eau + masque}.  Le système {bateau + eau + masque} de centre de masse G se déplace le long de l’axe Ox incliné d’un angle a par rapport à l’horizontale. A l’instant initial t = 0 s, le centre de masse G du système se trouve en O. Après une accélération constante pendant 100 s, le système atteint une vitesse limite V140 à la date t140 = 140 s. A.1. Donner la relation entre le vecteur accélération a(t)  et le vecteur vitesse v(t) puis en déduire, en justifiant la réponse, celle entre les normes a(t) et v(t). Le vecteur vitesse est une primitive du vecteur accélération. Suivant l'axe Ox ; v(t) = a t + Cste. A t = 0 ; v =0. v(t) = a t .  A.2. En analysant la courbe suivante, montrer que l’accélération du système est bien constante entre t0 = 0 s et t1 = 100 s et qu’elle vaut a0 = 1,20 × 10-2 m·s-2 . En déduire l'équation horaire de la vitesse v(t) du centre de masse G du système en fonction de a0 et t pour cette partie du mouvement. 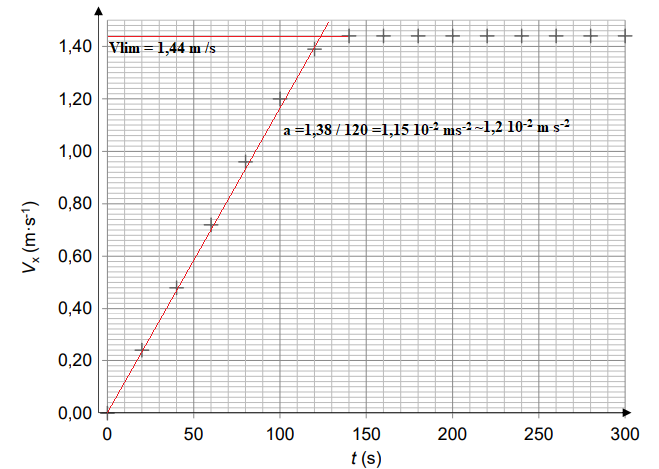Entre 0 et t = 100 s, les points sont alignés. La vitesse est une fonction linéaire de l'accélération. v = a0t = 1,2 10-2 t.  A.3. Montrer que l'équation horaire de la position x(t) du centre d'inertie G s’écrit entre t0 = 0 s et t1 = 100 s : x(t) = 0,5 × a0 × t 2 . La position est une primitive de la vitesse. x = 0,5 a0 t2 +Cste. A t = 0, x =0, d'où : x(t) = 0,5 × a0 × t 2 . 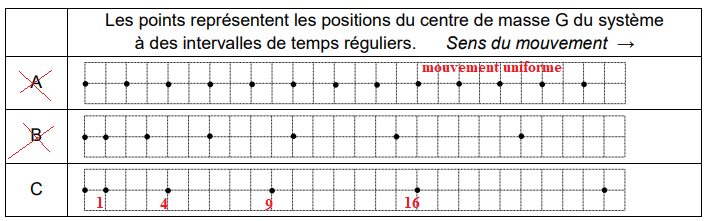A.4. Parmi les chronophotographies A, B et C suivantes, indiquer celle qui pourrait convenir pour le mouvement du système entre t0 = 0 s et t1 = 100 s. Justifier la réponse. A t= 1 s ; x1 = 6 10-3 m. A  t= 2 s ; x2 =4 x1. A  t= 3 s ; x2 =9 x1. B. Étude dynamique du mouvement du système {bateau + eau + masque}.  Le système {bateau + eau + masque}, de centre de masse G, en se déplaçant le long de la pente d’axe Ox est soumis à quatre actions modélisées par quatre forces : son poids, la réaction normale de la pente, la force des automotrices, et la force de frottement du masque et de l’eau le long de la pente. 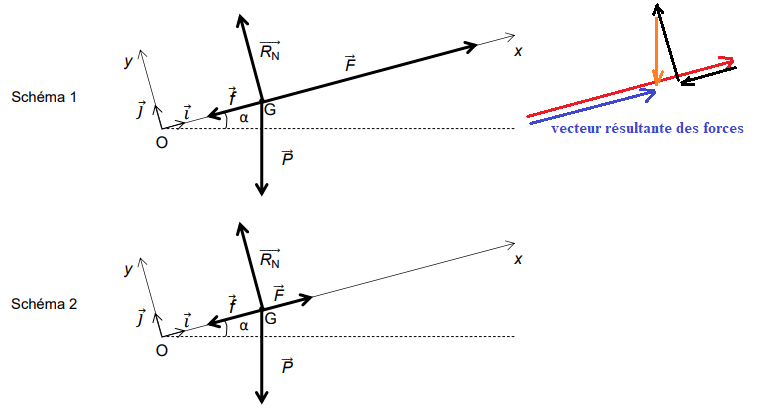Deux schémas représentés ci-dessous sont proposés pour modéliser la situation mécanique entre t0 = 0 s et t1 = 100 s : B.1. Déterminer le schéma qui représente le mieux la situation. Justifier la réponse en associant chaque vecteur force aux quatre forces décrites précédemment et en représentant la construction vectorielle de la somme des forces. Le schéma 1 convient : la résultante des vecteurs forces est dirigée selon Ox et dans le sens de l'axe. Le schéma 2 est à rejeter : la résultante des vecteurs forces est dirigée selon Ox et dans le sens contraire de l'axe. On s’intéresse maintenant à la phase du mouvement comprise entre t2 = 140 s et t3 = 300 s. B.2. Déterminer la nature du mouvement entre t2 et t3 et en déduire la valeur de la somme vectorielle des forces. Le mouvement étant rectiligne uniforme, la somme vectorielle des forces est nulle ( première loi de Newton). C. Observation du bateau à l’aide d’une lunette astronomique artisanale.  Dans le cadre d’une sortie scolaire sur le site, un professeur de physique demande à ses élèves d’observer le bateau avec une lunette astronomique artisanale depuis une passerelle suffisamment éloignée de celui-ci pour le considérer à l’infini. La lunette est constituée de deux tubes coulissants gradués en centimètres dans lesquels, deux lentilles convergentes L1 et L2 de distances focales respectives f ’1 et f ’2, sont placées aux extrémités. Le bateau est représenté par objet réel A∞B∞, A étant sur l’axe optique. C.1. Identifier la lentille qui constitue l’oculaire et celle qui constitue l’objectif. La consigne du professeur est de construire une lunette astronomique artisanale de grossissement G tel que G = 6.  Donnée : distance focale des lentilles disponibles : 5,0 cm, 10,0 cm, 12,5 cm, 20,0 cm, 30,0 cm.  C.2. Après avoir établi l’expression du grossissement de la lunette astronomique artisanale, prévoir, parmi les lentilles disponibles, celles qu’il faudra utiliser pour L1 et pour L2. 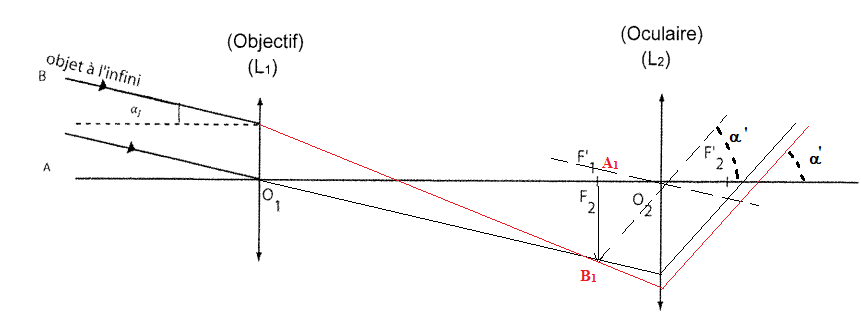Expression de G en fonction de f '1 et f '2. Triangle O1A1B1 : tan a ~ a =A1B1 / f '1. Triangle O2A1B1 : tan a' ~ a' =A1B1 / f '2 Par suite G = a' / a.= f '1 / f '2. L1  : f '1 = 30,0 cm et L2 : f '2 = 5,0 cm. Préciser également le réglage des tubes en indiquant les graduations du tube 1 et du tube 2 qui doivent coïncider. Le foyer image F '1 de L1 doit coïncider avec le foyer objet F2 de L2. La graduation 30 du tube 1 doit coïncider avec la graduation 5 du tube 2.

menu