Etude d'une exoplanète, bac Amérique du Nord 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... En 2019, Michel Mayor et Didier Queloz obtiennent le prix Nobel pour la découverte en 1995 d’une exoplanète, nommée 51Peg_b, orbitant autour d’une étoile de type solaire, nommée 51Peg_a.  Données : - distance entre la Terre et l’étoile 51Peg_a : DTerre-51Peg_a = 4,53 × 1017m ; - masse de l’étoile 51Peg_a : M51Peg_a = 1,89 × 1030 kg ; - masse du Soleil : MSoleil = 1,989 × 1030 kg ; - constante de gravitation universelle : G = 6,6742 × 10-11 m3 ∙s -2 ∙kg-1 . A. Étude du système double 51Peg Dans le cas du système double, constitué de l’exoplanète 51Peg_b et de son étoile 51Peg_a, les deux astres orbitent chacun autour du centre de masse B du système double. L’étoile 51Peg_a est animée d’un mouvement circulaire uniforme autour de B qui se manifeste par une variation de la coordonnée de son vecteur-vitesse selon l’axe de visée.  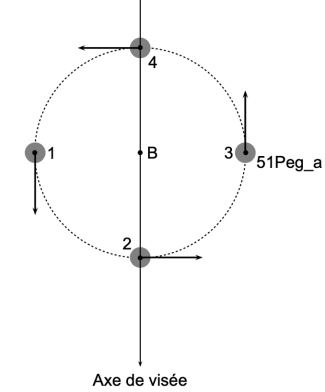Sur la figure suivante, le vecteur-vitesse de l’étoile est représenté par une flèche. Sa coordonnée selon l’axe de visée est : positive et maximale pour la position 1 ; nulle pour les positions 2 et 4 ; négative et minimale pour la position 3. On détecte la variation de la coordonnée de ce vecteur-vitesse à travers l’effet induit sur le spectre lumineux de l’étoile. Cette coordonnée varie de façon périodique : la période correspond également à la période de révolution de l’exoplanète autour de son étoile. A.1. Mesurer, avec le plus de précision possible, la période de révolution T de l’exoplanète 51Peg_b autour de son étoile. 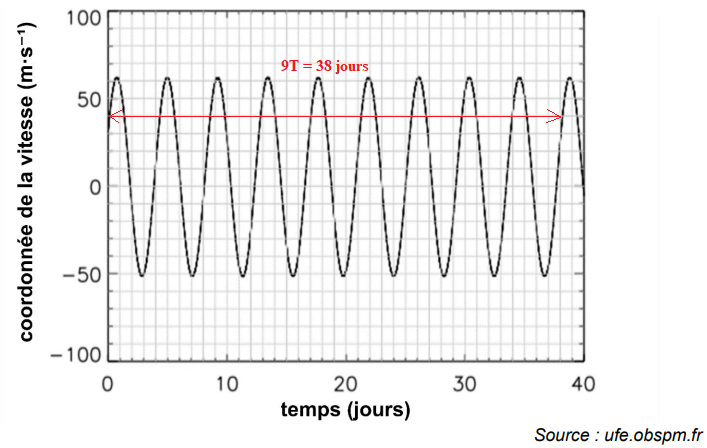T = 38 / 9 =4,2 jours.  Le mouvement de 51Peg_b autour de son étoile est un mouvement circulaire uniforme vérifiant la troisième loi de Kepler. Par application de cette loi, on montre que la valeur de la distance r séparant la planète 51Peg_b de son étoile est égale à 7,5 × 106 km. A.2. Choisir, en argumentant, parmi les quatre expressions suivantes celle qui correspond à la troisième loi de Kepler pour la situation étudiée. L’argumentation devra s’appuyer notamment sur une analyse dimensionnelle. T2 / a3 s'exprime en s2 m-3. G M51Pega s'exprime en m3 ∙s -2 ∙kg-1 kg soit m3 ∙s -2 ; 1 / (G M51Pega) s'exprime en s2 m-3. A.3. Retrouver la valeur de la distance r séparant la planète 51Peg_b de son étoile. T = 4,2 x24 x3600 =3,63 105 s. 4p2 / (G M51Pega) =4 x3,142 / (6,67 10-11 x1,89 1030)=3,13 10-19 s2 m-3. r3 = (3,63 105)2 / (3,13 10-19) =4,21 1029 ; r =7,5 109 m = 7,5 106 km.  Dans le système solaire, la planète Mercure est la plus proche du Soleil. Elle décrit une orbite quasicirculaire de rayon égal à 5,8 × 107 km en 88 jours. A.4. Comparer les caractéristiques du système double constitué de l’exoplanète 51Peg_b et son étoile 51Peg_a à celles du système Mercure-Soleil. Rapport des distances à l'astre central : ~ 10. Rapport des périodes de révolution : ~88 / 4,2 ~21. B. La lunette astronomique et exoplanète Le système exoplanétaire, constitué de l’étoile 51Peg_a et de son exoplanète 51Peg_b, est observé depuis la Terre. On se pose la question de savoir s’il est possible de distinguer 51Peg_a et 51Peg_b à l’œil nu ou à travers une lunette pour astronome amateur. L’œil peut distinguer deux objets si l’angle de séparation est au minimum de 3,0 × 10-4 rad. 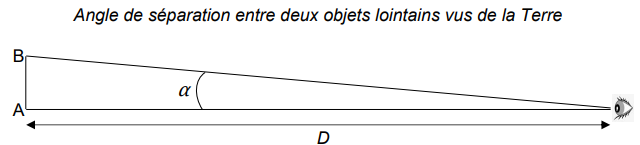Pour des objets lointains, comme les étoiles, l’angle a qui sépare deux objets A et B vus de la Terre est donné par : a = AB  / D .L’angle est exprimé en radian.  B.1. Indiquer si l’on peut distinguer 51Peg_a de 51Peg_b à l’œil nu. a = 7,5 × 109  / (4,53 × 1017) =1,7 10-8 rad. Cette valeur étant inférieure au pouvoir séparateur de l'oeil, on ne peut pas distinguer 51Peg_a de 51Peg_b.  Une lunette astronomique d’amateur est constituée d’un objectif de distance focale f '1  égale à 900 mm et de plusieurs oculaires de distances focales f ' 2 : 6,0 mm ; 10,0 mm ; 20,0 mm.  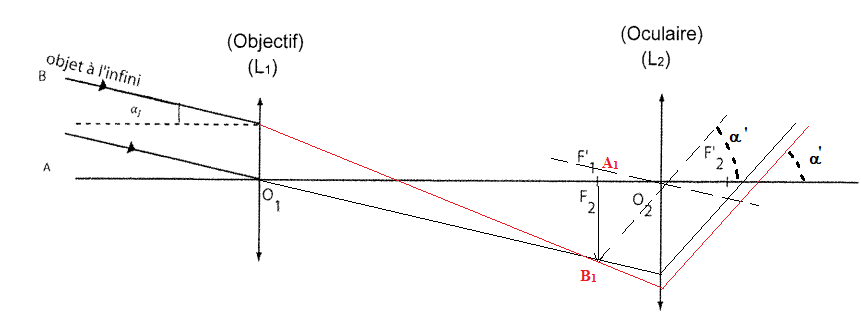Un schéma de cette lunette astronomique se trouve sur le document suivant. B.2. Compléter le schéma du document , avec le trajet de la lumière et faire apparaître l’angle a ′ sous lequel est vu le système double quand on l’observe avec la lunette astronomique. On considère que l’étoile 51Peg_a est dans la direction de l’axe optique des lentilles de la lunette. B.3. Établir l’expression du grossissement de la lunette en fonction de la distance focale de l’objectif et de la distance focale de l’oculaire. Triangle O1A1B1 : tan a ~ a =A1B1 / f '1. Triangle O2A1B1 : tan a' ~ a' =A1B1 / f '2 Par suite G = a' / a.= f '1 / f '2.  B.4. En détaillant le raisonnement, indiquer si l’on peut distinguer 51Peg_b de son étoile à l’aide du matériel disponible. Grossissement maximal : 900 / 6,0 =150. a' = G a =150 x 1,7 10-8 =2,6 10-6 rad. Cette valeur étant toujours inférieure au pouvoir séparateur de l'oeil, on ne peut pas distinguer 51Peg_a de 51Peg_b.

menu