Mathématiques, géométrie, Bac Amérique du Nord 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans l’espace muni d’un repère orthonormé  d’unité 1 cm, on considère les points suivants :  J(2 ; 0 ; 1), K(1 ; 2 ; 1) et L(−2 ; −2 ; −2) . 1. a. Montrer que le triangle JKL est rectangle en J. JK= [(1-2)2+(2-0)2+(1-1)2 ]½=(1+4+0)½ = 5½. JL= [(-2-2)2+(-2-0)2+(-2-1)2 ]½=(16+4+9)½ = 29½. KL= [(-2-1)2+(-2-2)2+(-2-1)2 ]½=(9+16+9)½ = 34½. KL2 = JL2 +JK2; le triangle JKL est rectangle en J.  b. Calculer la valeur exacte de l’aire du triangle JKL en cm2 . JL x JK=(5 x29)½ / 2 = 145½ / 2 cm2.  c. Déterminer une valeur approchée au dixième près de l’angle géométrique JKL. tan (JKL) =JL / KJ =(29 /5)½ ~2,408 ; L'angle JKL mesure 67,5 °. 2. a. Démontrer que le vecteur n de coordonnées (6 ; 3 ; -10) est un vecteur normal au plan (JKL). 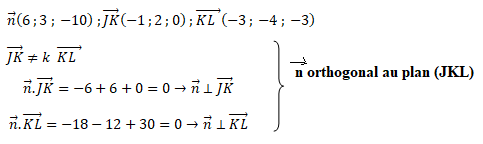b. En déduire une équation cartésienne du plan (JKL). 6x+3y-10z+d=0.   J(2 ; 0 ; 1) appartient à ce plan : 12+0-10+d=0 ; d = -2. 6x+3y-10z-2=0. Dans la suite, T désigne le point de coordonnées (10 ; 9 ; −6). 3. a. Déterminer une représentation paramétrique de la droite D orthogonale au plan (JKL) et passant par T. Le vecteur n(6 ; 3 ; -10) est un vecteur directeur de la droite D. x = 6t +xT =6t+10. y = 3t+yT =3t +9. z = -10t +zT =-10 t-6.  b. Déterminer les coordonnées du point H, projeté orthogonal du point T sur le plan (JKL).  H appartient au plan(JKL) : 6xH+3yH-10zH-2=0. H appartien à la droite D : xH = 6t +10. yH = 3t+9. zH = -10t -6. 6(6t+10)+3(3t+9)-10(-10t-6)-2=0 ; 145 t +145=0 ; t = -1. xH=4 ; yH =6 ; zH =4.  c. On rappelle que le volume V d’un tétraèdre est donné par la formule : V = 1 3 B ×h où B désigne l’aire d’une base et h la hauteur correspondante. Calculer la valeur exacte du volume du tétraèdre JKLT en cm3 . Hauteur TH =[ (4-10)2 +(6-9)2 +(4-(-6)2]½ =(36+9+100)½ =145½. Aire de base ( aire du triangle JKL) =145½ / 2. V = 145½ x145½ / 6 = 145 / 6 cm3. ... .... Une exposition d’art contemporain a lieu dans une salle en forme de pavé droit de largeur 6 m, de longueur 8 m et de hauteur 4 m. Elle est représentée par le parallélépipède rectangle OBCDEFGH où OB = 6 m, OD = 8 m et OE = 4 m. Dans ce repère on a, en particulier C(6; 8; 0), F(6; 0; 4) et G(6; 8; 4). Une des œuvres exposées est un triangle de verre représenté par le triangle ART qui a pour sommets A(6; 0; 2), R(6; 3; 4) et T(3; 0; 4),  Enfin, S est le point de coordonnées ( 3 ; 5 / 2 ; 0) .  1. a. Vérifier que le triangle ART est isocèle en A. AR=[(6-6)2+(3-0)2 +(4-2)2]½ =13½. AT=[(3-6)2+(0-0)2 +(4-2)2]½ =13½. AR = AT : le triangle ART est isocèle en A.  b. Calculer le produit scalaire suivant. c. En déduire une valeur approchée à 0,1 degré près de l’angle (ART).  2. a. Justifier que le vecteur n(2 ; -2 ; 3) est un vecteur normal au plan (ART).  b. En déduire une équation cartésienne du plan (ART). 2x-2y+3z +d=0 A(6 ; 0 ; 2) appartient à ce plan : 12+0+6+d=0 ; d = -18. 2x-2y+3z -18=0.  3. Un rayon laser dirigé vers le triangle ART est émis du plancher à partir du point S. On admet que ce rayon est orthogonal au plan (ART).  a. Soit D la droite orthogonale au plan (ART) et passant par le point S. Justifier que le système ci-dessous est une représentation paramétrique de la droite D : x = 3+2k ; y = 2,5 -2k ; z =3k avec k réel. Le vecteur n de coordonnées (2 ; -2 ; 3) est un vecteur directeur de cette droite. x = 2k+xS =2k+3. y =-2k+yS = -2k+2,5. z = 3k+zS=3k. b. Soit L le point d’intersection de la droite D, avec le plan (ART). Démontrer que L a pour coordonnées ( 5 ; 1 /2 ; 3) . L appartient à cette droite : xL = -2k+3 ; yL = -2k+2,5 ; zL =3k. L appartient au plan (ART) : 2xL-2yL+3zL -18=0. 2(2k+3)-2(-2k+2,5)+3(3k)-18=0 17k-17=0 ; k = 1. L( 5 ; 0,5 ; 3).  4. L’artiste installe un rail représenté par le segment [DK] ou K est le milieu du segment [EH]. Sur ce rail, il positionne une source lumineuse laser en un point N du segment [DK] et il oriente ce second rayon laser vers le point S. a. Montrer que, pour tout réel t de l’intervalle [0; 1], le point N de coordonnées (0 ; 8−4t ; 4t) est un point du segment [DK].   xK=( xE+xH) /2 =0 ; yK=( yE+yH) /2 =4 ; zK=( zE+zH) /2 =4 . b. Calculer les coordonnées exactes du point N tel que les deux rayons laser représentés par les segments [SL] et [SN] soient perpendiculaires. Coordonnées du point N : (0 ; 8-17/5 =23 /5 ; 17 / 5).

menu