Mathématiques,
probabilités, Bac Amérique du Nord
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Probabilités.
Chaque chaque jour où il travaille, Paul doit se rendre à la gare pour
rejoindre son lieu de travail en
train. Pour cela, il prend son vélo deux fois sur trois et, si il ne
prend pas son vélo, il prend sa voiture.
1. Lorsqu’il prend
son vélo pour rejoindre la gare, Paul ne rate le train qu’une fois sur
50 alors que,
lorsqu’il prend sa voiture pour rejoindre la gare Paul rate son train
une fois sur 10.
On considère une journée au hasard lors de laquelle Paul sera à
la gare pour prendre le train
qui le conduira au travail.
On note :
V l’évènement « Paul prend son vélo pour rejoindre la gare »;
R l’évènement « Paul rate son train ».
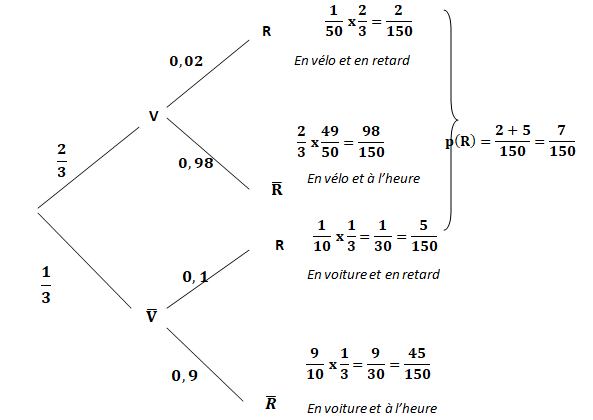
a. Faire un arbre
pondéré résumant la situation.
b. Montrer que la
probabilité que Paul rate son train est égale à 7
/150
.
 c.
c. Paul a raté son
train. Déterminer la valeur exacte de la probabilité qu’il ait pris son
vélo
pour rejoindre la gare.
P R(V) =P(R n V) / P(R) =2 / 150 / (7 /150) = 2 /7.
2. On choisit au hasard
un mois pendant lequel Paul s’est rendu 20 jours à la gare pour
rejoindre
son lieu de travail selon les modalités décrites en préambule.
On suppose que, pour chacun de ces 20 jours, le choix entre le vélo et
la voiture est indépendant
des choix des autres jours.
On note X la variable aléatoire donnant le nombre de jours où Paul
prend son vélo sur ces 20
jours.
a. Déterminer la loi
suivie par la variable aléatoire X. Préciser ses paramètres.
On répète 20 expériences identiques et indépendantes, n'ayant que deux
issues.. Il s'agit donc d'un schéma de bernoulli.
X suit une loi binomiale de paramètre n=20 et p =2 /3.
b. Quelle est la
probabilité que Paul prenne son vélo exactement 10 jours sur ces 20
jours
pour se rendre à la gare ? On arrondira la probabilité cherchée à 10 −3
.
P(X=10 )= ( 2010) x (2/3) 10 x
(1/3) 10=0,054.
c. Quelle est la
probabilité que Paul prenne son vélo au moins 10 jours sur ces 20 jours
pour
se rendre à la gare ?
P(X>10 )= 1 -P(X <10) =
1-P(X < 9) =0,962.
.
d. En moyenne,
combien de jours sur une période choisie au hasard de 20 jours pour se
rendre à la gare, Paul prend-il son vélo ? On arrondira la réponse à
l’entier.
Espérance E(X) =n p = 20 x2 /3 = 40 /3 ~13,3 soit 14 fois.
3. Dans le cas où Paul se
rend à la gare en voiture, on note T la variable aléatoire donnant le
temps de trajet nécessaire pour se rendre à la gare. La durée du trajet
est donnée en minutes, arrondie
à la minute. La loi de probabilité de T est donnée par le tableau
ci-dessous :
k
(min)
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
|
P(T=k)
|
0,14
|
0,13
|
0,13
|
0,12
|
0,12
|
0,11
|
0,10
|
0,08
|
0,07
|
|
k
x P(T=k)
|
1,4
|
1,43
|
1,56
|
1,56
|
1,68
|
1,65
|
1,6
|
1,36
|
1,26
|
Total =13,5
|
Déterminer l’espérance de la variable aléatoire T et interpréter
cette valeur dans le contexte de
l’exercice.
Espérance : 13,5 .
Il met en moyenne 13,5 minutes pour se rendre à la gare en
voiture..
|
...
|
....
|
Probabilités.
Dans une région touristique, une société propose un service de location de vélos pour la journée.
La société dispose de deux points de location distinctes, le point A et le point B. Les vélos peuvent
être empruntés et restitués indifféremment dans l’un où l’autre des deux points de location.
On admettra que le nombre total de vélos est constant et que tous les matins, à l’ouverture du service,
chaque vélo se trouve au point A ou au point B.
D’après une étude statistique :
- Si un vélo se trouve au point A un matin, la probabilité qu’il se trouve au point A le matin suivant
est égale à 0,84;
- Si un vélo se trouve au point B un matin la probabilité qu’il se trouve au point B le matin suivant
est égale à 0,76.
À l’ouverture du service le premier matin, la société a disposé la moitié de ses vélos au point A, l’autre
moitié au point B.
On considère un vélo de la société pris au hasard.
Pour tout entier naturel non nul n, on définit les évènements suivants :
- An : « le vélo se trouve au point A le n-ième matin »
- Bn : « le vélo se trouve au point B le n-ième matin ».
Pour tout entier naturel non nul n, on note an la probabilité de l’évènement An et bn la probabilité
de l’évènement Bn.
Ainsi a1 = 0,5 et b1 = 0,5.
1. Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les deux premiers matins :
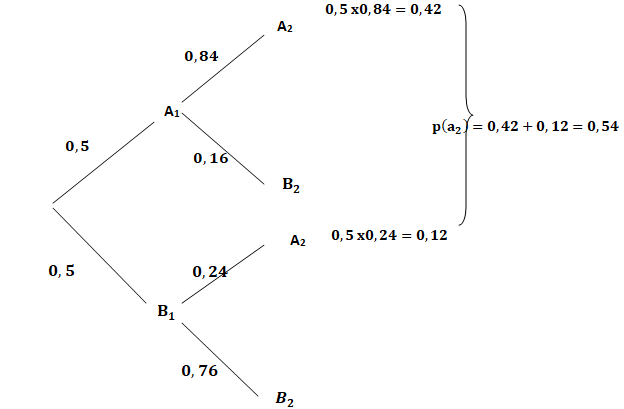
2. a. Calculer a2.
b. Le vélo se trouve au point A le deuxième matin. Calculer la probabilité qu’il se soit trouvé
au point B le premier matin. La probabilité sera arrondie au millième.
PA2(B1)=P(A2 n B1) / P(A2)=0,12 / 0,54 =0,222.
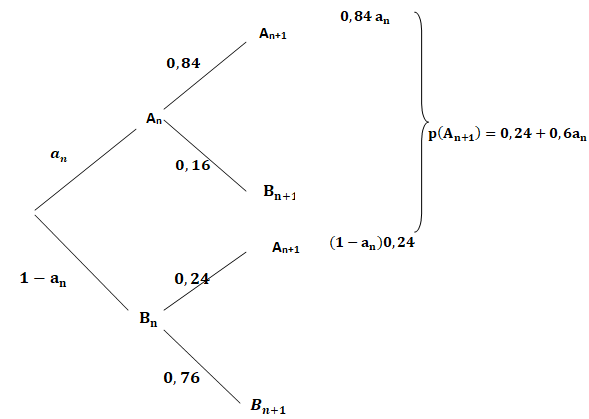
3. a. Recopier et compléter l’arbre pondéré ci-dessous qui modélise la situation pour les n-ième et n +1-ième matins.
b. Justifier que pour tout entier naturel non nul n, an+1 = 0,6an +0,24.
4. Montrer par récurrence que, pour tout entier naturel non nul n, an = 0,6−0,1×0,6n−1
.
Initialisation :a1 =0,6-0,1 x0,60=0,5. La propriété est vraie au rang 1.
Hérédité : an = 0,6−0,1×0,6n−1
est suppopsée vraie.
an+1 = 0,24 +0,6 an.
an+1 = 0,24 +0,6 (0,6−0,1×0,6n−1 )
an+1 = 0,24 +0,36 −0,1×0,6n=0,6−0,1×0,6n−1
.
La propriété est vraie au rang n+1.
Conclusion : La propriété est vraie au rang 1 et héréditaire, elle est vraie pour tout n entier naturel.
5. Déterminer la limite de la suite (an) et interpréter cette limite dans le contexte de l’exercice.
-1 < 0,6 < 1, donc 0,6n tend vers zéro si n tend vers l'infini.
an tend vers 0,60.
Au bout d'un temps assez long, la probabilité qu'un vélo soit à la station A est de 0,60.
6. Déterminer le plus petit entier naturel n tel que an > 0,599 et interpréter le résultat obtenu
dans le contexte de l’exercice.
0,6−0,1×0,6n−1 > 0,599.
0,6-0,599 > 0,1×0,6n−1 .
0,001 / 0,1 > 0,6n−1 .
0,01 > 0,6n−1 .
ln(0,01) > (n-1) ln(0,6)
n-1 > ln(0,01) / ln(0,6)
n-1 > 9,05 ; n > 10,05.
La probabilité qu'un vélo se trouve au point A est supérieure à 0,599 à partir du 11-ième jour.
QCM. Question 4
Un sac contient 20 jetons jaunes et 30 jetons bleus.
On tire successivement et avec remise 5 jetons du
sac.
La probabilité de tirer exactement 2 jetons jaunes, arrondie au
milllième, est :
a. 0,683 ; b. 0,346 ; c.
0,230 ; d. 0,165.
Schéma de Bernoulli ( 5 expériences aléatoire n'ayant que deux issues,
identiques et indépendantes entre elles).
On note X la variable aléatoire donnant le nombre de jetons
jaunes tirés. X suit une loi binomiale de paramètres n = 5 et p = 20
/50 = 0,4.
p(X=2) =(52) x0,42 x(1-0,4)3
= 0,346.
Question 5
Un sac contient 20 jetons jaunes et 30 jetons bleus. On tire
successivement et avec remise 5 jetons du
sac.
La probabilité de tirer au moins un jeton jaune, arrondie au milllième,
est :
a. 0,078 ; b. 0,259 ; c. 0,337 ; d. 0,922.
Même question que la question 4.
p(X > 1) = 1
-p(X=0) = 1-0,65 = 0,922.
Question 6
Un sac contient 20 jetons jaunes et 30 jetons bleus.
On réalise l’expérience aléatoire suivante : on tire successivement et
avec remise cinq jetons du sac.
On note le nombre de jetons jaunes obtenus après ces cinq tirages.
Si on répète cette expérience aléatoire un très grand nombre de fois
alors, en moyenne, le nombre de
jetons jaunes est égal à :
a. 0,4; b. 1,2 ; c.
2 ; d. 2,5.
Espérance d'une loi binomiale E = n p = 5 x0,4 = 2.
|
|