Mathématiques,
suite, fonction, Bac Amérique du Nord
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Suite.
On
considère la suite (Tn) définie par : T0 = 180 et pour tout n entier naturel, Tn+1 =
0,955Tn +0,9.
1. a. Démontrer par récurrence que, pour tout entier naturel n, Tn > 20.
Initialisation : T0 = 180, la propriété est vraie au rang zéro.
Hérédité : Tn+1 > 20 est supposée vraie.
0,955 Tn+1 > 20 x0,955 =19,9.
0,955 Tn+1 +0,9 > 19,9 +0,9 =20,8.
Tn+2 > 20,8.
Tn+2 > 20.
Conclusion : la propriété est vraie au rang zéro et héréditaire, elle est donc vraie pour tout entier n.
b. Vérifier que pour tout entier naturel n, Tn+1−Tn = −0,045(Tn −20). En déduire le sens de
variation de la suite (Tn).
Tn+1−Tn = 0,955Tn +0,9−Tn = -0,045Tn+0,9 = -0,045(Tn-0,9 / 0,045) = −0,045(Tn −20).
Tn étant supérieur ou égal à 20; Tn-20 >0.
Tn+1−Tn < 0, la suite est décroissante.
c. Conclure de ce qui précède que la suite (Tn) est convergente. Justifier.
La suite est décroissante etminorée par 20, donc elle converge.
2. Pour tout entier naturel n, on pose : un = Tn −20.
a. Montrer que la suite (un) est une suite géométrique dont on précisera la raison.
un+1 = Tn+1-20 = 0,955Tn +0,9.-20 =0,995 Tn-19,1.
un+1 = 0,955(Tn-19,1 / 0,955) =0,955(Tn-20) = 0,955 un.
(un) est une suite géométrique de raison q = 0,955 et de premier terme u0 =160.
b. En déduire que pour tout entier naturel n, Tn = 20+160×0,955n
.
un = 160 x0,955n= Tn-20.
Tn = 20+160×0,955n
.
c. Calculer la limite de la suite (Tn).
-1 < 0,955 < 1, donc 0,955n tend vers zéro si n tend vers plus l'infini.
Tn tend vers 20.
d. Résoudre l’inéquation Tn < 120 d’inconnue n entier naturel.
20+160×0,955n < 120.
160×0,955n < 100.
0,955n < 5 /8.
n ln(0,955) < ln(5 / 8).
n > ln(5 / 8) / ln(0,955) soit n >11.
3. Dans cette partie, on s’intéresse à l’évolution de la température au centre d’un gâteau après sa
sortie du four.
On considère qu’à la sortie du four, la température au centre du gâteau est de 180° C et celle de
l’air ambiant de 20° C.
La loi de refroidissement de Newton permet de modéliser la température au centre du gâteau
par la suite précédente (Tn). Plus précisément, Tn représente la température au centre du gâteau, exprimée en degré Celsius, n minutes après sa sortie du four.
a. Expliquer pourquoi la limite de la suite (Tn) déterminée à la question 2. c. était prévisible
dans le contexte de l’exercice.
Au bout d'un temps suffisamment long la température au centre du gâteau sera égale à la température du milieu extérieur.
b. On considère la fonction Python ci-dessous :
def temp(x) :
T = 180
n = 0
while T > x :
T=0.955*T+0.9
n=n+1
return n
Donner le résultat obtenu en. exécutant la commande temp(120).
Interpréter le résultat dans le contexte de l’exercice.
L'algorithme donne le temps au bout duquel la température au centre du gâteau sera inférieure à 120°C.
Soit 11 minutes d'après la question précédente.
Fonction exponentielle.
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Justifier chaque réponse.
1. Affirmation 1 : Pour tout réel x :
1−
(1−e
x) /
(1+e
x
)=
2
/(1+e
−x). Vrai.
Réduire au même dénominateur :
[1+ex-(1-ex) /
(1+e
x
)=2ex /
(1+e
x
)= 2 / (e-x+1)
2. On considère la fonctiong définie sur R par g (x) =
e
x/(
e
x +1)
.
Affirmation 2 : L’équation g (x) =
1/
2
admet une unique solution dans R. Vrai.
0,5 = e
x/(
e
x +1)
.
ex+1 = 2ex.
1 = ex ; x = 0.
3. On considère la fonction f définie sur R par f (x) = x
2
e
−x
et on note C sa courbe dans un repère
orthonormé.
Affirmation 3 : L’axe des abscisses est tangent à la courbe C en un seul point.
Vrai.
Dériver en posant u = x2 et v = e-x ; u' = 2x ; v' = -e-x.
u'v+v'u = 2x e-x-x2e-x =xe-x(2-x).
Coeficient directeur de la tangente ( l'axe des abscisses) à la courbe : zéro.
Equation de l'axe des abscisses : y = 0.
f '(x) = 0 donne x = 0 et x = 2.
Si x=0, équation de la tangente y = f '(0) x +b = b.
Le point de coordonnée (0 ; f(0) =0 appartient à la tangent, d'où b = 0. ( convient )
Si x=2, équation de la tangente y = f '(0) x +b = b.
Le point de coordonnée (2 ; f(2) =4e-2 appartient à la tangent, d'où b = 4e-2. ( Ne convient pas)
4. On considère la fonction h définie sur R par h(x) = e
x (
1− x
2)
.
Affirmation 4 : Dans le plan muni d’un repère orthonormé, la courbe représentative de la fonction h n’admet pas de point d’inflexion. Faux.
Dériver en posant u = ex et v = 1-x2 ; u' = ex ; v' = -2x.
h '(x) =(1-x2) ex -2xex =ex(1-x2-2x).
dériver à nouveau en posant u = ex, v = 1-2x-x2.
u' = ex ; v' = -2x-2.
h"(x) = ex(1-x2-2x)-(2x+2)ex = -ex(1+x2-4x).
1+x2-4x = 0 ; discriminant D =(-4)2-4 = 12, soit deux solutions réelles.
h"(x) s'annule deux fois et change de signe : donc 2 points d'inflexion.
5. Affirmation 5 : La limite en plus l'infini de ex / (ex+x) est égale à zéro. Faux.
ex / (ex+x) = 1 / (1+x /ex).
Par croissance comparée, x / ex tend vers zéro si x tend vers plus l'infini.
ex / (ex+x) tend vers 1 en plus l'infini.
6. Affirmation 6 : Pour tout réel x, 1+e
2x > 2ex
.
1+e
2x - 2ex > 0.
(1-ex)2 > 0 est vraie.
|
...
|
....
|
Fonction exponentielle.
Partie A.
Soit p la fonction définie sur l’intervalle [−3 ; 4] par :
p(x) = x
3 −3x
2 +5x +1
1. Déterminer les variations de la fonction p sur l’intervalle [−3 ; 4].
p '(x) = 3x2-6x+5.
3x2-6x+5 =0 ; discriminant D = 36-4*3*5= -24 aucune racine réelles.
p'(x) > 0 et p(x) est strictement croissante.
2. Justifier que l’équation p(x) = 0 admet dans l’intervalle [−3 ; 4] une unique solution qui sera
notée ß.
p(-3) =-27-27-15+1= -68.
p(4) = 64-48+20+1=37.
p(x) est continue et strictement croissante de -68 à 37.
0 appartient à cet intervalle ; d'après le corollaire du htéorème des
valeurs intermédiaires, l'équation p(x) = 0 admet une solution unique
dans l'intervalle [-3 ; 4].
3. Déterminer une valeur approchée du réel ß au dixième près.
La calculatrice donne ß ~-0,2.
4. Donner le tableau de signes de la fonction p sur l’intervalle [−3 ; 4].
Si x appartient à [-3 ; ß [, p(x) est strictement négative.
si x = ß, p(x) est nulle.
Si x appartient à [ß ; 4 [, p(x) est strictement positive.
Partie B
Soit f la fonction définie sur l’intervalle [−3 ; 4] par :
f (x) =
e
x
/( 1+ x
2).
On note Cf sa courbe représentative dans un repère orthogonal.
1. a. Déterminer la dérivée de la fonction f sur l’intervalle [−3 ; 4].
On pose u = ex; v = 1+x2 ; u' = ex ; v' = 2x.
(u'v-v'u) / v2 =ex(1+x2-2x) / (1+x2)2 = ex(1-x)2 / (1+x2)2 .
b. Justifier que la courbe Cf admet une tangente horizontale au point d’abscisse 1.
La dérivée s'annule en x = 1.
Equation de la tangent : y = f(1) = e / 2.
2. Les concepteurs d’un toboggan utilisent la courbe Cf comme profil d’un toboggan. Ils estiment
que le toboggan assure de bonnes sensations si le profil possède au moins deux points d’inflexion.
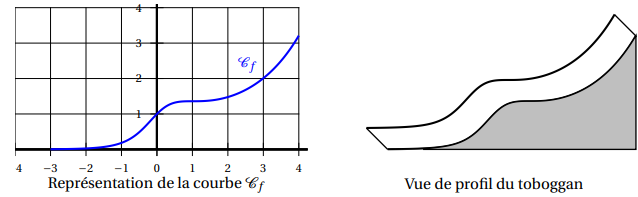
a. D’après le graphique ci-dessus, le toboggan semble-t-il assurer de bonnes sensations ?
Argumenter.
f est convexe sur [-3 ; 0], concave sur [0 : 1] et convex sur [1 ; 4].
La courbe admet deux points d'inflexion en x = 0 et x = 1.
Le tobogan assure de bonnes sensations.
b. On admet que la fonction f
′′, dérivée seconde de la fonction f , a pour expression pour
tout réel x de l’intervalle [−3 ; 4] :
f
′′(x) =
p(x)(x −1)ex /(
1+ x
2 )3
où p est la fonction définie dans la partie A.
En utilisant l’expression précédente de f
′′, répondre à la question : « le toboggan assuret-il de bonnes sensations ? ». Justifier.
ex /(
1+ x
2 )3 est positif.
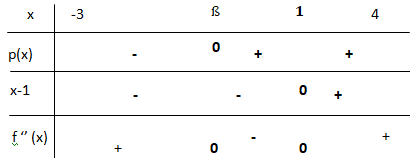
f "(x) s'annule en x = 1 et change de signe.
p(x) s'annule en x = ß et change de signe.
Il existe deux points d'inflexion : le tobogan assure de bonnes sensations.
QCM.
Question 1
Le réel a est définie par a = ln(9)+ln(1/3½)
+ln(1/9)
est égal à :
a. 1−
1
2
ln(3) ; b.
1/
2
ln(3) ; c. 3ln(3)+
1
/2 ; d. −
1
/2
ln(3).
a = ln(9 /(9 x3½)=ln(1/3½) = 0,5 ln(1/3) = -0,5 ln(3).
Question 2
On note (E) l’équation suivante lnx +ln(x −10) = ln 3+ln 7 d’inconnue le réel x.
a. 3 est solution de (E).
b. 5− 46½ est solution de (E).
c. L’équation (E) admet une unique solution réelle.
d. L’équation (E) admet deux solutions réelles.
ln(x(x-10) )= ln (21).
x(x-10) = 21 ; x2-10x-21 = 0 avec x > 10.
Discriminant D = 102 +4*21=184 = 22* 46
x1 = (10 +2*46½) / 2 = 5+46½.
x1 =(10 -2*46½) / 2 = 5-46½.( valeur inférieure à 10, ne convient pas).
Question 3
La fonction f est définie sur l’intervalle ]0 ; +∞[ par l’expression f (x) = x
2
(−1+ln x).
On note Cf sa courbe représentative dans le plan muni d’un repère.
a. Pour tout réel x de l’intervalle ]0 ; +∞[, f
′
(x) = 2x +
1
/x
.
b. La fonction f est croissante sur l’intervalle ]0 ; +∞[.
c. f
′ (
e½ )
est différent de 0.
d. La droite d’équation y = −
1
/2
e est tangente à la courbe Cf au point d’abscisse e½. Vrai.
On dérive en posant u = x2 , v = -1+ln(x) ; u' = 2x ; v' = 1 /x.
f '(x) = 2x(-1+ln(x) +x = x ( -1+2ln(x)).
f '(e½)=e½(-1+1)=0.
f(e½)=e(-1+0,5) = -e /2.
.
Question 4
Un sac contient 20 jetons jaunes et 30 jetons bleus. On tire successivement et avec remise 5 jetons du
sac.
La probabilité de tirer exactement 2 jetons jaunes, arrondie au milllième, est :
a. 0,683 ; b. 0,346 ; c. 0,230 ; d. 0,165.
Schéma de Bernoulli ( 5 expériences aléatoire n'ayant que deux issues, identiques et indépendantes entre elles).
On note X la variable aléatoire donnant le nombre de jetons
jaunes tirés. X suit une loi binomiale de paramètres n = 5 et p = 20
/50 = 0,4.
p(X=2) =(52) x0,42 x(1-0,4)3 = 0,346.
Question 5
Un sac contient 20 jetons jaunes et 30 jetons bleus. On tire successivement et avec remise 5 jetons du
sac.
La probabilité de tirer au moins un jeton jaune, arrondie au milllième, est :
a. 0,078 ; b. 0,259 ; c. 0,337 ; d. 0,922.
Même question que la question 4.
p(X > 1) = 1 -p(X=0) = 1-0,65 = 0,922.
Question 6
Un sac contient 20 jetons jaunes et 30 jetons bleus.
On réalise l’expérience aléatoire suivante : on tire successivement et avec remise cinq jetons du sac.
On note le nombre de jetons jaunes obtenus après ces cinq tirages.
Si on répète cette expérience aléatoire un très grand nombre de fois alors, en moyenne, le nombre de
jetons jaunes est égal à :
a. 0,4; b. 1,2 ; c. 2 ; d. 2,5.
Espérance d'une loi binomiale E = n p = 5 x0,4 = 2.
|
|