Atterrissage du premier étage d'une fusée, bac G Amérique du Sud 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Une technologie spatiale développée par une société commerciale permet de récupérer le premier étage d’une fusée après son décollage. Après la séparation entre le premier et le second étage, le premier revient sur Terre pour atterrir délicatement sur une plateforme. Cet atterrissage doit s’effectuer « en douceur », c’est-à-dire avec une valeur de la composante verticale de la vitesse inférieure à 6 m·s-1. Cet exercice se propose d’étudier le retour sur Terre du premier étage de la fusée. Le premier étage de la fusée chute dans l’atmosphère terrestre depuis une altitude de plusieurs dizaines de kilomètres. Pour ralentir sa chute, il utilise son moteur. On étudie le mouvement de cet étage à proximité du sol après le déploiement du train d’atterrissage. Lors de cette dernière phase, sa masse est considérée comme constante. Disposant d’une vidéo de l’atterrissage du premier étage d’une fusée, un pointage des positions du point M a été réalisé et a permis d’obtenir les graphiques 1 et 2 ci-après. On a représenté ci-dessous deux positions successives du point M aux dates t1 = 0,50 s et t2 = 2,50 s lors de la phase de l’atterrissage du premier étage. Celui-ci se trouve alors respectivement aux altitudes 𝑦1 et 𝑦2. Le mouvement est étudié dans le référentiel terrestre supposé galiléen. Lors de la dernière phase de l’atterrissage, le mouvement du système est vertical et s’effectue selon l’axe O𝑦 orienté suivant la verticale ascendante. 1. Représenter sur un schéma le vecteur vitesse du point M aux instants t1 et t2 en utilisant l’échelle de représentation suivante : 1 cm sur votre feuille correspond à 6,0 m·s−1. 2. Déterminer la valeur de l’accélération et commenter le signe de la projection de l’accélération suivant Oy. Qualifier le mouvement. a = (v(2,5) - v(0,5)) / (t2-t1) =(-6,6 +12,2) / (2,5-0,5) =2,8 m s-2. L'accélération a le sens de l'axe Oy. La vitesse diminue, le mouvement est uniformément freiné. ... .... 3. Représenter, sur un schéma, les forces qui modélisent les principales actions qui s’exercent sur le premier étage de la fusée étudiée de manière à rendre compte du signe de la projection de l’accélération suivant Oy. Justifier. La fusée est soumise à son poids P = mg et à l'action des moteurs notée F, verticale vers le haut, norme supérieure à mg.. 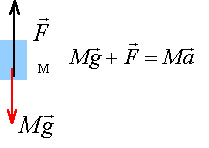4. En exploitant les graphiques, montrer que l’équation horaire 𝑦 = f(t) du mouvement du point M peut s’écrire : y= 1,40 t2 − 13,6 t + 33 avec y en m et t en s. vy(t) = 2,8 t-13,6. La position est une primitive de la vitesse : y(t) = 1,4 t2-13,6 t+ Constante. 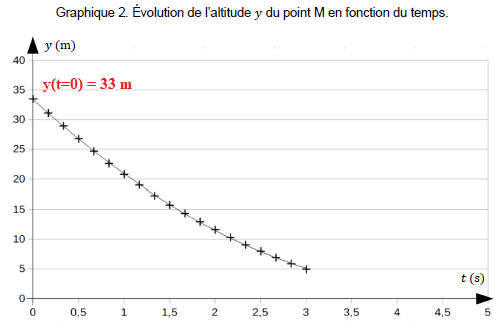y(t=0) = 33 = A. 5. Déterminer la valeur de la vitesse du système lorsqu’il touche le sol en admettant que l’accélération ne varie pas sur les derniers mètres. 0= 1,40 t2 − 13,6 t + 33. Discriminant D =(-13,6)2 -4 x33 x1,4=0,16 =0,42. Solutions :  t =(13,6 -0,4) / 2,8 =4,71 s et t =(13,6 +0,4) / 2,8 =5 s. v(4,71) = 2,8 x4,71 -13,6 = -0,41 m /s. v(t =5) =2,8 x5 -13,6 = 0,4 m /s (valeur positive,ne pas retenir, en désaccord avec le graphe 1). 6. Préciser si l’atterrissage s’effectue « en douceur ». La vitesse au sol étant inférieure à 6 m /s, l'atterrissage s'effectue en douceur.

menu