Mathématiques, fonction logarithme,  Bac Amérique du Sud 9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le but de cet exercice est d’étudier la fonction f , définie sur ]0 ; +∞[ ,par :  f (x) = 3x − x ln(x)−2ln(x).  PARTIE A : Étude d’une fonction auxiliaire g Soit g la fonction définie sur ]0 ; +∞[ par g(x) = 2(x −1)− x ln(x). On note g ′ la fonction dérivée de g. On admet que la limite en plus l'infini de g(x) est −∞. 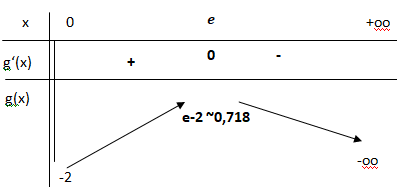1. Calculer g(1) et g(e). g(1) = 2(1-1)-ln(1) = 0. g(e) = 2(e-1) -e ln(e) = 2e-2-e = e-2. 2. Déterminer la limite en 0+ de  g(x) en justifiant votre démarche. 2(x-1) tend vers -2. ln(x) tend vers moins l'infini. x ln(x) tend vers 0. g(x) tend vers -2.  3. Montrer que, pour tout x > 0, g ′ (x) = 1−ln(x). En déduire le tableau des variations de g sur ]0 ; +∞[. On pose u = x, v = ln(x) ; u' = 1 ; v' = 1 /x. u'v+v'u = ln(x) +1. Par suite g'(x) = 2-(1+ln(x) = 1-ln(x). Si x appartient à ]0 ; e[, g'(x) > 0 et g(x) est croissante. Si x appartient à ]e ; +oo[, g'(x) < 0 et g(x) est décroissante. Si x = e, g'(x) = 0 et g(x) présente un maximum. 4. Montrer que l’équation g(x) = 0 admet exactement deux solutions distinctes sur ]0 ; +∞[ : 1 et a avec a appartenant à l’intervalle [e ; +∞[. On donnera un encadrement de a à 0,01 près. Sur ]0 ; e[ la fonction g(x) est dérivable donc continue. -2 < 0 < e : d'après le théorème des valeurs intermédiaires, il existe un unique réel ß tel que g(ß)= 0. Or g(1) = 0, donc ß = 1. Sur ]e ; +oo[ la fonction g(x) est dérivable donc continue.  g(x) décroît de 0,718 à -oo, il existe donc un unique réel a tel que g(a)= 0. Or g(4,92) ~0,0009 et g(4,93)~-0,005, donc a appartient à ]4,92 ; 4,93[. 5. En déduire le tableau de signes de g sur ]0 ; +∞[. 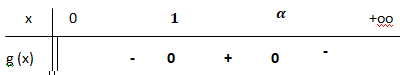PARTIE B : Étude de la fonction f On considère dans cette partie la fonction f , définie sur ]0 ; +∞[,par f (x) = 3x − x ln(x)−2ln(x). On note f ′ la fonction dérivée de f . 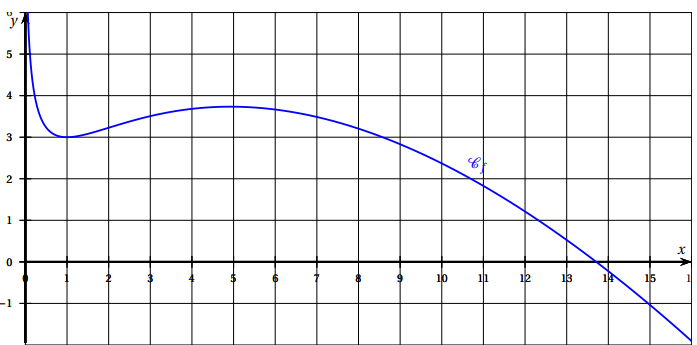La représentation graphique Cf de cette fonction f est donnée ci-dessous. On admet que la limite de f(x) en zéro est plus l'infini. 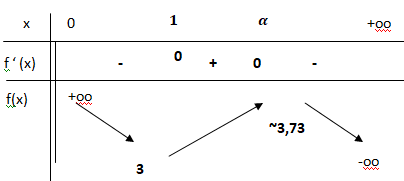1. Déterminer la limite de f en +∞ en justifiant votre démarche. f(x) = x( 3-ln(x)-2 ln(x) / x)). En plus l'infini : par croissance comparée ln(x) / x tend vers zéro ; ln(x) tend vers plus l'infini ; 3-ln(x) tend vers moins l'infini ; par produit des limites, f(x) tend vers moins l'infini. 2. a. Justifier que pour tout x > 0, f ′ (x) = g(x). Dérivée de x ln(x) : ln(x) +1. f '(x) = 3-(ln(x)+1)-2/x =3-1-ln(x)-2 /x = 2-ln(x) -2 /x =(2x-ln(x)-2) / x =g(x) / x. b. En déduire le tableau des variations de f sur ]0 ; +∞[. x étant positif, le signe de f'(x) est celui du numérateur. 3. On admet que, pour tout x > 0, la dérivée seconde de f , notée f ′′, est définie par f ′′(x) = (2− x) / x 2 . Étudier la convexité de f et préciser les coordonnées du point d’inflexion de Cf . f "(x) s'annule et change de signe en x= 2. f "(x) >0 sur ]0 ; 2[ et f(x) est convexe. f "(x) <0 sur ]2 ; +oo[ et f(x) est concave. Le point de coordonnées (2 ; f(2) ) est le point d'inflexion de la courbe. ... .... Soit g la fonction définie sur l’intervalle ]0 ; +∞[ par g(x) = 1+ x 2 [1−2ln(x)]. La fonction g est dérivable sur l’intervalle ]0 ; +∞[ et on note g ′ sa fonction dérivée. On appelle C la courbe représentative de la fonction g dans un repère orthonormé du plan.  PARTIE A 1. Justifier que g(e) est strictement négatif. g(e) = 1+e2(1-2ln(e)) =1+e2(1-2)=1+e2(1-2)=(-1)(1+e2). 2. Justifier que la limite de g(x) en plus l'infini est -oo. En plus l'infini : ln(x) tend vers plus l'infini ; 1-2ln(x) tend vers moins l'infini ; par produit des limites, x 2 [1−2ln(x)] tend vers moins l'infini. 3. a. Montrer que, pour tout x appartenant à l’intervalle ]0 ; +∞[, g ′ (x) = −4x ln(x). On pose u = x2; v = 1-2 ln(x) ; u' = 2x ; v' = -2 /x. u'v+v'u = 2x(1-2ln(x) -2x = -4x ln(x).  b. Étudier le sens de variation de la fonction g sur l’intervalle ]0 ; +∞[ Si x appartient à ]0 ; 1[, g'(x) > 0 et g(x) est croissante. Si x appartient à ]1 ; +oo[, g'(x) < 0 et g(x) est décroissante. Si x = 1, g'(x) = 0 et g(x) présente un maximum. c. Montrer que l’équation g(x) = 0 admet une unique solution, notée ß, sur l’intervalle [1 ; +∞[. Sur ]1 ; +oo[ la fonction g(x) est dérivable donc continue.  g(x) décroît de 2 à -oo, il existe donc un unique réel ß tel que g(ß)= 0. d. Donner un encadrement de ß d’amplitude 10−2 . Or g(1,89) ~0,024 et g(1,90)~-0,024, donc ß appartient à ]1,89 ; 1,90[. 4. Déduire de ce qui précède le signe de la fonction g sur l’intervalle [1 ; +∞[. PARTIE B  1. On admet que, pour tout x appartenant à l’intervalle [1 ; α], g ′′(x) = −4[ln(x)+1]. Justifier que la fonction g est concave sur l’intervalle [1 ; ß]. ln (x) >0 ; ln(x) +1 >0 ;  g "(x) < 0 ;  g est concave sur [1 ; ß]. 2. Sur la figure ci-dessous, A et B sont les points de la courbe C d’abscisses respectives 1 et ß.  a. Déterminer l’équation réduite de la droite (AB). A(1 ; 2 )  appartient à la droite (AB) : yA = axA+b ; 2 = a+b. B(ß ; g(ß=0) ) appartient à la droite (AB) : yB = axB+b ; 0 = aß+b soit b = -aß. Par suite 2 =a-aß=a(1-ß) ; a = 2/(1-ß) ; b = 2-a = 2-2 /(1-ß) =-2ß /(1-ß). y = 2x /(1-ß) -2ß /(1-ß).  b. En déduire que pour tout réel x appartenant à l’intervalle [1 ; ß], g(x) > -2x /(ß-1) +2ß/(ß-1). Sur cet intervalle, g(x) est concave, sa courbe représentative se situe au dessus de toutes sécantes, donc au dessus du segment [AB]. Donc g(x) > -2x /(ß-1) +2ß/(ß-1)..

menu