Mathématiques,
probabilités, Bac Amérique du Sud 9 / 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
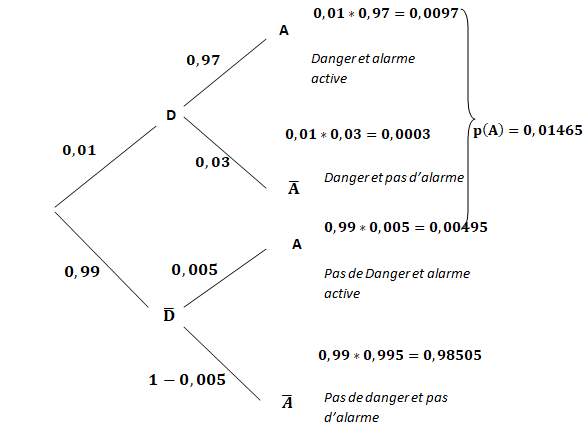
PARTIE A.
Le système d’alarme d’une entreprise fonctionne de telle sorte
que, si un danger se présente,
l’alarme s’active avec une probabilité de 0,97.
La probabilité qu’un danger se présente est de 0,01 et la
probabilité que l’alarme s’active est
de 0,01465.
On note A l’évènement « l’alarme s’active » et D l’événement « un
danger se présente ».
1.
Représenter la situation par un arbre pondéré qui sera complété au fur
et à mesure de
l’exercice.
2. a. Calculer la
probabilité qu’un danger se présente et que l’alarme s’active.
0,01 x0,97 = 0,0097.
b. En déduire la
probabilité qu’un danger se présente sachant que l’alarme s’active.
Arrondir le résultat à 10 −3
.
P A(D) = P(A n D) / (PA) =0,0097 / 0,01465 =0,662.
3. Montrer que la
probabilité que l’alarme s’active sachant qu’aucun danger ne s’est
présenté est 0,005.
P non D(A) =P(non D n A) / P(non D).
Formule des probabilités totales : P(A) = P(A n D) + P( non D n A).
P( non D
n A) = 0,01465 -0,0097 =0,00495.
Pnon
D(A) =0,00495 / 0,99 =0,005.
4. On
considère qu’une alarme ne fonctionne pas normalement lorsqu’un danger
se présente et qu’elle ne s’active pas ou bien lorsqu’aucun danger ne
se présente et qu’elle
s’active.
Montrer que la probabilité que l’alarme ne fonctionne pas normalement
est inférieure
à 0,01.
P(non D n
A) = P(A n D) + P( D n non A) =0,00495 +0,0003 =0,00525 < 0,01.
PARTIE B.
Une usine fabrique en grande quantité des systèmes d’alarme. On
prélève successivement
et au hasard 5 systèmes d’alarme dans la production de l’usine. Ce
prélèvement est assimilé
à un tirage avec remise.
On note S l’évènement « l’alarme ne fonctionne pas normalement » et on
admet que
P(S) = 0,00525.
On considère X la variable aléatoire qui donne le nombre de systèmes
d’alarme ne fonctionnant pas normalement parmi les 5 systèmes d’alarme
prélevés.
Les résultats seront arrondis à 10 −4
.
1. Donner la
loi de probabilité suivie par la variable aléatoire X et préciser ses
paramètres.
X suit une loi binomiale de paramètres n = 5 et p = 0,00525.
2. Calculer la
probabilité que, dans le lot prélevé, un seul système d’alarme ne
fonctionne
pas normalement.
P(X = 1) = ( 5 1) * 0,00525 1
*(1-0,00525) 5-1~0,00257.
3. Calculer la
probabilité que, dans le lot prélevé, au moins un système d’alarme ne
fonctionne pas normalement.
P(X > 1) =
1-P(X=0)=1- (5 0) * 0,005250 *(1-0,00525)5-0~0,0260.
PARTIE
C.
Soit n un entier naturel non nul. On prélève successivement et au
hasard n systèmes d’alarme.
Ce prélèvement est assimilé à un tirage avec remise.
Déterminer le plus petit entier n tel que la probabilité d’avoir, dans
le lot prélevé, au moins
un système d’alarme qui ne fonctionne pas normalement soit supérieure à
0,07.
La variable aléatoire Y donnant le nombre d'alarmes défectueuses suit
la loi binomiale de paramètres n et p = 0,00525.
P(Y > 1) >0,07.
1-P(Y = 0) > 0,07 ; 1-0,07 > P(Y=0) ; P(Y=0) < 0,93.
(n 0) * 0,005250 *(1-0,00525)n < 0,93.
0,99475n < 0,93.
n ln(0,99475) < ln(0,93).
-0,00526 n < -0,0726 ; n > 13,8.
Il faut prélever au moins 14 système d'alarmes.
|
...
|
....
|
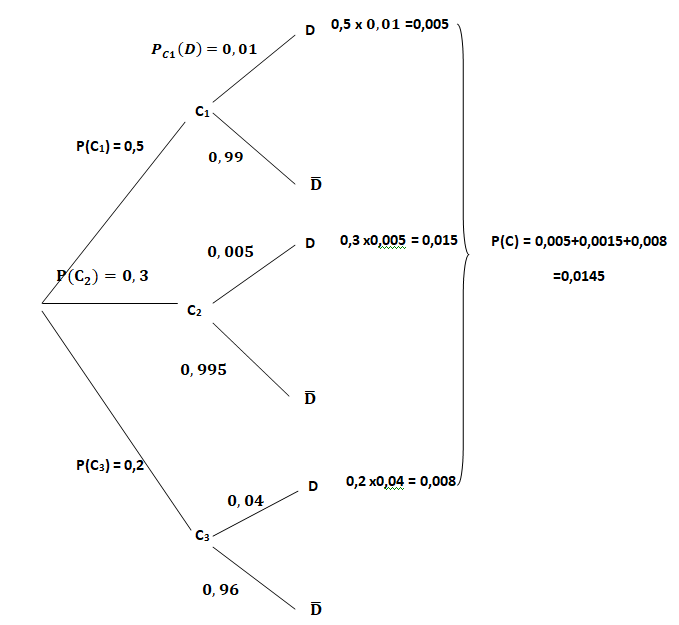
Une entreprise fabrique des composants pour l’industrie automobile. Ces composants sont
conçus sur trois chaînes de montage numérotées de 1 à 3.
• La moitié des composants est conçue sur la chaîne n° 1;
• 30 % des composants sont conçus sur la chaîne n° 2;
• les composants restant sont conçus sur la chaîne n° 3.
À l’issue du processus de fabrication, il apparaît que 1 % des pièces
issues de la chaîne n°1 présentent un défaut, de même que 0,5 % des
pièces issues de la chaîne n°2 et 4 % des pièces
issues de la chaîne n°3.
On prélève au hasard un de ces composants.
On note :
• C1 l’événement « le composant provient de la chaîne n° 1 »;
• C2 l’événement « le composant provient de la chaîne n° 2 »;
• C3 l’événement « le composant provient de la chaîne n° 3 »;
• D l’événement « le composant est défectueux».
Dans tout l’exercice, les calculs de probabilité seront donnés en valeur décimale exacte ou arrondie à 10−4
si nécessaire.
PARTIE A
1. Représenter cette situation par un arbre pondéré.
2. Calculer la probabilité que le composant prélevé provienne de la chaîne n° 3 et soit
défectueux.
0,2 x0,04 = 0,008.
3. Montrer que la probabilité de l’événement D est P(D) = 0,0145.
4. Calculer la probabilité qu’un composant défectueux provienne de la chaîne n° 3.
PC3(D) = P(C3 n D) / P(D) =0,008 / 0,0145 ~0,05517.
PARTIE B
L’entreprise décide de conditionner les composants produits en
constituant des lots de n
unités. On note X la variable aléatoire qui, à chaque lot de n unités,
associe le nombre de
composants défectueux de ce lot.
Compte tenu des modes de production et de conditionnement de
l’entreprise, on peut considérer que X suit la loi binomiale de
paramètres n et p = 0,0145.
1. Dans cette question, les lots possèdent 20 unités. On pose n = 20.
a. Calculer la probabilité pour qu’un lot possède exactement trois composants défectueux.
P(X = 3) = (20 3) * 0,01453
*(1-0,0145)20-3~0,0027.
b. Calculer la probabilité pour qu’un lot ne possède aucun composant défectueux.
En déduire la probabilité qu’un lot possède au moins un composant défectueux.
P(X = 0) = (20 0) * 0,01450
*(1-0,0145)20-0~0,7467.
P(X > 1) = 1-P(X=0) =1-0,7467 ~0,2533.
2. Le directeur de l’entreprise souhaite que la probabilité de n’avoir aucun composant
défectueux dans un lot de n composants soit supérieure à 0,85.
Il propose de former des lots de 11 composants au maximum. A-t-il raison ? Justifier la
réponse.
P(X = 0) = (11 0) * 0,01450
*(1-0,0145)11-0~0,8516.
Le directeur a donc raison.
PARTIE C
Les coûts de fabrication des composants de cette entreprise sont de 15
euros s’ils proviennent
de la chaîne de montage n° 1, 12 euros s’ils proviennent de la chaîne
de montage n° 2 et 9 euros s’ils proviennent de la chaîne de montage n°
3.
Calculer le coût moyen de fabrication d’un composant pour cette
entreprise.
0,5 * 15 +0,3 *12 +0,2 *9 = 12,9 € pour un composant.
|
|