L'incroyable saut sans parachute de Lucky Luke, bac STL Mayotte 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Le 30 juillet 2016, le cascadeur Américain Luke Aikins, surnommé Lucky Luke, s'est jeté d'un avion à 7 620 m d'altitude sans aucun équipement pour ralentir sa chute vertigineuse. Il a ainsi battu le précédent record de saut sans parachute. L’excès de vent représente le plus grand danger pour Luke Aikins, c'est pourquoi ses équipes ont lancé un ballon-sonde quelques heures avant le saut afin de recueillir un maximum de données météorologiques. Le ballon-sonde météorologique s'élève jusqu'à une altitude généralement comprise entre 20 et 30 kilomètres au-dessus du sol de son lieu de lancement. En montant, le ballon grossit et finit par éclater. Après éclatement, un petit parachute s'ouvre pour ramener la nacelle et son matériel scientifique au sol. D'après :https://fr.wikipedia.org/wiki/Luke_Aikins.  Dans une première partie nous allons étudier l’ascension de ce ballon météorologique puis dans une seconde partie, nous analyserons le mouvement de Luke Aikins. Données :  l’expression littérale de la norme du vecteur qui modélise la poussée d’Archimède exercée sur un corps de volume V dans l’air est la suivante : FA = rair ∙ V g  avec :  rair la masse volumique de l’air au sol et, dans les conditions normales de pression et de température, 1,22 kg ∙ m−3 ; -V le volume de la partie immergée du corps plongé dans l’air ;  l’expression littérale de la norme du vecteur qui modélise la force de frottement fluide s’exerçant sur un corps en mouvement dans l’air est la suivante : f = k ∙ v2 avec : k le coefficient de trainée ; k = 0,31 kg ∙ m−1 ; v la vitesse du centre d'inertie du système. Partie A : Étude de l’ascension d’un ballon sonde météorologique.  L'objectif de cette partie est d'étudier le mouvement du système constitué par le ballon, le parachute, le réflecteur, la nacelle et l’antenne dans le référentiel terrestre supposé galiléen. Ce système est représenté sur la figure ci-dessous à faible altitude, sur les premières centaines de mètres. Ainsi, on peut considérer que l'intensité de la pesanteur g le volume du ballon V et la masse volumique de l'air restent constants. Lors du décollage du ballon-sonde, on se placera dans un cas idéal où :  il n'y a pas de vent ;  le mouvement s'effectue dans la direction verticale vers le haut ;   le mouvement est accéléré au début de l’envol ;  le volume des autres éléments constituant le ballon sonde est négligeable par rapport au volume du ballon.  Données : masses des différentes parties du système : ballon : 1,53 kg ; nacelle et antenne : 3,80 kg ; réflecteur radar : 0,22 kg ; parachute : 0,15 kg. 1. Déterminer la valeur du poids du système. Masse totale : 1,53 +3,80 +0,22 +0,15 =5,7 kg. Poids mg = 5,7 x9,81 ~56 N.  Le bilan des forces extérieures appliquées au centre de gravité M du système est représenté ci-après. 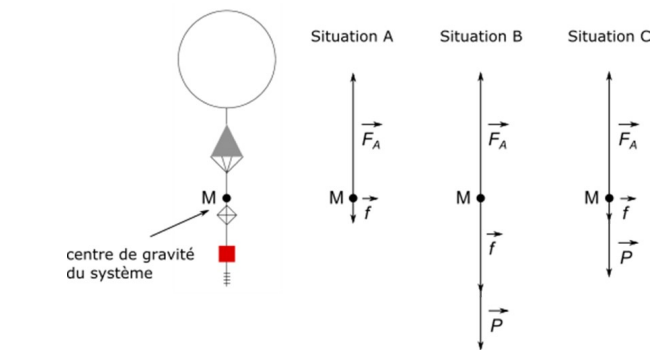2. Identifier, parmi les 3 situations schématisées ci-dessus, laquelle correspond à la représentation correcte, compte tenu des hypothèses formulées en justifiant votre réponse. Situation A : il manque le poids. Situation B : la somme vectorielle des forces est dirigée vers le bas ( pas de décollage). La situation C est correcte.  3. Déterminer la valeur FA de la poussée d’Archimède, sachant que le volume du ballon est de V = 9,0 m3. Comparer à la valeur du poids et conclure. FA =1,22 x 9,0 x9,81 ~ 108 N supérieure au poids, on peut décoller.  4. En appliquant au système la seconde loi de Newton, établir que l’expression littérale de l’accélération du système étudié selon l’axe Oz orienté vers le haut, peut s’écrire sous la forme : az = -g +(FA-f) / m. Ecrire la seconde loi de Newton sur l'axe vertical ascendant. -mg + FA-f = maz. az = -g +(FA-f) / m. Au cours de l'ascension, le ballon sonde atteint un régime permanent où il se déplace verticalement et à vitesse constante. 5. Justifier que l’accélération du système est nulle en régime permanent. Le mouvement étant rectiligne uniforme, la somme vectorielle des forces est nulle ( première loi de Newton). En conséquence l'accélération est nulle. 6. En déduire alors la valeur de la vitesse limite atteinte par le système. mg = FA -f = FA-0,31 v2. 0,31 v2 =FA -mg =108 -56=52. v2=52 / 0,31=167,7 ; vlimite ~ 13 m /s.    ... .... Partie B : Étude du mouvement de Luke Aikins Une fois les données recueillies, Luke Aikins peut alors effectuer son saut sans parachute d'une hauteur H de 7 620 mètres. À sa réception, il va être ralenti par un filet de réception de 30 mètres sur 30 mètres. Durant sa chute qui a duré environ deux minutes, il a rapidement atteint une vitesse limite de l'ordre de 200 km∙h-1. On étudie le mouvement du système {Luke Aikins} en chute verticale dans le référentiel terrestre considéré comme galiléen. On choisit un axe Oz vertical orienté toujours vers le bas, dont l'origine O est située au point de départ. À la date t = 0 s, date du début du saut, la vitesse de Luke Aikins dans le référentiel terrestre est nulle. On négligera la poussée d'Archimède. L’évolution de la valeur de la vitesse v de chute de Luke Aikins au cours du temps est représentée sur le graphe suivant. Dans les premières secondes de chute, on considère que le système est en chute libre, c’est-à-dire que la seule force extérieure qui s’y applique est son poids . 7. Donner l’expression vectorielle de la seconde loi de Newton appliquée à ce système.  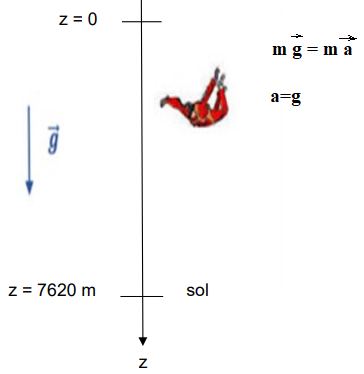8. Montrer, dans l’hypothèse de la chute libre, que l’équation horaire de la coordonnée selon Oz de la vitesse du système {Luke Aikins} est : vz =gt. La vitesse est une primitive de l'accélération. v = gt +constante. A l'instant initial, la vitesse est nulle. vz = gt. 9. À partir de la courbe, estimer jusqu’à quel instant le modèle de la chute libre peut rendre compte de la réalité du saut réalisé par Luke Aikins.  10. Déterminer graphiquement la valeur de la vitesse de chute de Luke Aikins en régime permanent. Comparer à la valeur de la vitesse limite annoncée : 200 km.h-1. 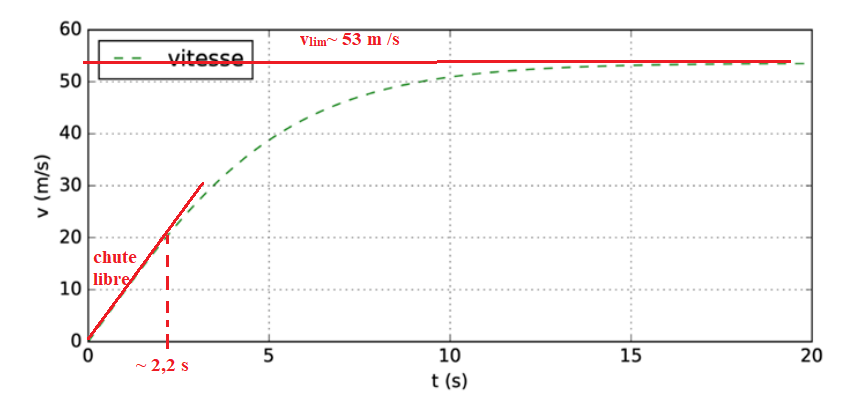Vitesse limite : 53 m /s ou 53 x3,6 ~191 km /h. Ecart avec 200 km /h : (200-191) / 200 =0,045  (4,5 %). Donc accord avec la vitesse limite anoncée.

menu