Mathématiques,
le carbure de silicium, bac STL Mayotte 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Mathématiques.
Pour les questions 1 et 2 uniquement :
On donne, ci-dessous Ch, la courbe représentative d’une fonction h, définie et dérivable
sur l’intervalle [−5 ; 5]. On a tracé une partie de la droite, notée T, tangente à la courbe Ch au point d’abscisse −2.
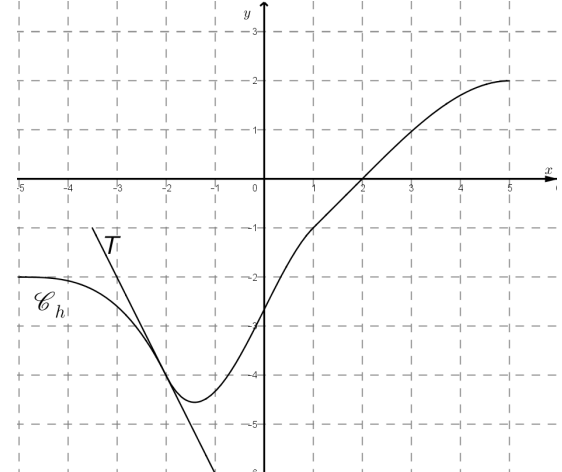
1. Les points A (−3 ; −2) et B ( −2 ; −4) appartiennent à la droite T.
a) Déterminer l’équation réduite de la droite T.
y = ax +b.
yA = axA+b soit :-2 = -3a+b.
yB = axB+b soit :-4 = -2a+b.
Par suite : -2 -(-4) = -3a -(-2a) ; 2=-a, a =-2.
b = -2 +3a = -2 -6 = -8.
y = -2x-8.
b) En déduire la valeur exacte de h'(−2).
h'(-2) =coefficient directeur de la droite T soit -2.
c) Déterminer les coordonnées des points d’intersection de la droite T avec chacun des
axes du repère.
Avec l'axe horizontal : 0 = -2x-8 , x = -4.
Avec l'axe vertical : x=0 ; y = -8.
2. Exploitation du graphique
Soit H une primitive de h sur l’intervalle [−5 ; 5].
À l’aide du graphique, donner le sens de variation de la fonction H sur l’intervalle [−5 ; 5].
h est négative sur [-5 ; 2 ] : H est décroissante.
h est positive sur [2 ; 5 ] : H est croissante.
3.
On considère l’équation différentielle (E) suivante : y′ = −0,04y + 0,8 (E)
Déterminer f la solution de l’équation différentielle (E) sur l’intervalle [0 ; +∞ [, qui vérifie la
condition initiale f(0) = 100.
Solution générale de y' +0,04 y =0 : f (x)= A exp(-0,04 x) avec A une constante.
Solution particulière de (E) : y = 0,8 /0,04 =20.
Solution générale de (E) : f(x) = A exp(-0,04x) +20.
f(0) = 100 = A +20 ; A = 80.
f(x) = 80 exp(-0,04x) +20.
4.
Soit f la fonction définie et dérivable sur R par f(x) = (x+1)e-x.
.
a) Montrer que, pour tout x réel, f '(x)= -x e-x.
On pose u = x+1 et v = e-x ; u'=1 ; v' = -e-x.
u'v+v'u = e-x-(x+1)e-x= -xe-x.
b) En déduire les variations de f sur R.
e-x >0 ; si x appartient à ]-oo ; 0], f '(x) >0 et f est croissante.
si x appartient à [0 ; +oo[, f '(x) < 0 et f est décroissante.
Pour les questions 5 et 6 uniquement :
On note L le niveau sonore en dB et I l’intensité sonore en W∙ m−2 d’un son.
On désigne
par Log la fonction logarithme décimal. On a la relation suivante : L = 10 Log (I / I0), où I0 = 10−12 W∙ m−2 .
5 :
a) Quel est le niveau sonore L d’un son d’intensité sonore I = 10-5 W∙ m−2 ?
L = 10 log( 10-5 / 10-12) = 10 log(107) = 70 dB.
b) Une sirène d’alarme a un niveau sonore de 130 dB.
Quelle est son intensité sonore I ?
I = I0 10 L/10 =10-12 x 1013=10 W m2.
6 :
On souhaite faire baisser le niveau sonore de 10 dB.
On note L ′ = L − 10 et on noteI ′ l’intensité sonore correspondant à L' .
Exprimer I ′ en fonction de I.
L = 10 log (I / I0) ; L' = 10 log (I ' / I0) ;
10 log (I ' / I0) =10 log (I / I0) -10.
log (I ' / I0) = log (I / I0) -1.
log (I ' / I0) - log (I / I0) = -1.
log(I ' / I) = -1 ; I ' / I = 10-1.
|
...
|
....
|
Le carbure de silicium
On considère une enceinte vide, de volume constant, thermostatée à la température T2 = 1 200 K, dans laquelle, au temps t = 0 min, on introduit une certaine quantité de MTS.
À cette température, la transformation permettant la formation de carbure de silicium peut
être considérée comme totale.
L'équation de la réaction modélisant la transformation chimique au cours de laquelle le
MTS se décompose est la suivante :
CH3SiCl3(g) --> SiC(s) + 3 HCl(g)
On suit par un procédé adapté l’évolution de la concentration en MTS au cours du temps.
On obtient ainsi le graphe suivant.
1. Déterminer le temps de demi-réaction t½ dans ces conditions expérimentales en
expliquant votre démarche.
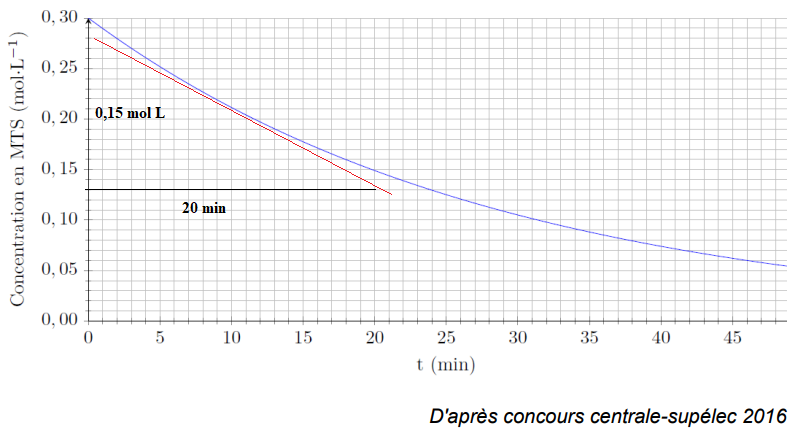
2. On rappelle que t½ = ln 2 / k
avec k la constante de vitesse de la réaction.
Déterminer la valeur de k dont on précisera l’unité.
k = ln 2 / t½ = ln 2 / 19 ~3,65 10-2 min-1.
3. Déterminer graphiquement la valeur de la vitesse de disparition du MTS à l’instant t = 10 min.
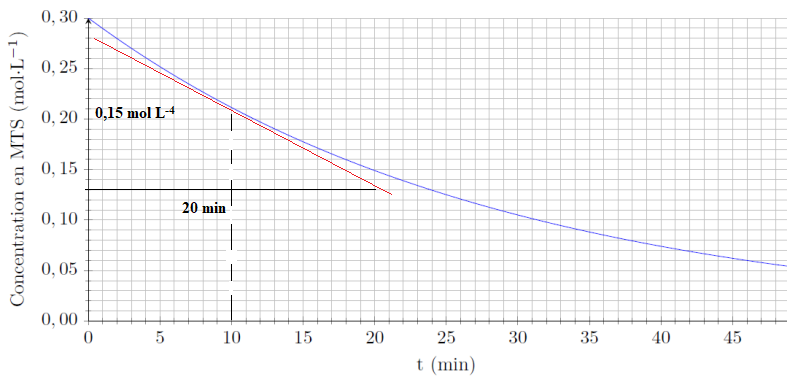
Valeur absolue du coefficient directeur de la tangente à la courbe à t = 10 min.
0,15 /20 = 7,5 10-3 mol L-1 min-1.
4. La vitesse de disparition du MTS est de 1,0 × 10−2 mol·L-1·min-1 à t = 1 min et de
3,5 × 0-3 mol L-1 min-1à t = 30 min.
Conclure en discutant de l’évolution au cours du temps de la vitesse de disparition
du MTS lorsque la concentration évolue.
Lorsque la concentration diminue, la vitesse de réaction diminue.
On modélise la concentration en MTS exprimée en mol·L-1 en fonction du temps t exprimé
en minute, par la fonction c, définie sur l’intervalle [ 0 ; 50 ] par :
c(t)= 0,30 ∙ exp(−0,035t )
5. On note c’ la fonction dérivée de la fonction c sur l’intervalle [ 0 ; 50 ].
Déterminer l’expression de c ’(t) pourt appartenant à [ 0 ; 50 ].
c'(t) = -0,30 x0,035 exp(−0,035t ) = -1,05 10-2 exp(−0,035t ).
6. On rappelle que la vitesse de disparition de MTS est égale à l’opposé de la fonction
dérivée c ’. On note c"’ la fonction dérivée de c ’.
On admet que c ’’(t) = 3,675. 10−4exp(−0,035t ) pourt appartenant à [ 0 ; 50 ].
Etudier le sens de variation de la vitesse de réaction au cours du temps.
Comparer le sens de variation avec le résultat de la question 4.
Le terme en exponentielle étant positif, c"(t) est positif. c'(t) est donc croissante et -c'(t) est décroissante.
La vitesse de la réaction diminue au cours du temps.
7. On considère que la transformation chimique de décomposition de MTS peut être
stoppée lorsqu’il ne reste que 10% de la concentration initiale de MTS.
Déterminer l’instant t à partir duquel la transformation chimique peut être stoppée.
On donnera la valeur exacte, puis la valeur arrondie à la minute près.
0,30 x0,1 = 0,030= 0,30 ∙ exp(−0,035t ).
0,1 = exp(−0,035t ).
ln(0,1) = -0,035t ;
t = - ln(0,1) / 0,035 ~66 min.
|
|