Chute
d'une bille dans un liquide,
premier navire à hydrogène, bac STL Métropole 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . | .
.
|
|
.
.
|
..
..
......
...
|
Lorsqu'un objet est
lâché dans un fluide (air, eau, etc.), il subit, outre son poids et la
poussée d'Archimède, des forces de frottement fluide. La modélisation
de ces forces de
frottement fluide conduit à considérer que :
- lorsque la vitesse de l’objet v est « faible », l’intensité des
forces de frottement fluide
est proportionnelle à v ;
- lorsque la vitesse de l’objet v est « élevée », l’intensité des
forces de frottement fluide
est proportionnelle à v2
.
Dans cet exercice, on se propose d’étudier expérimentalement le modèle
des forces de
frottement fluide dans le cas des faibles vitesses.
Étude expérimentale
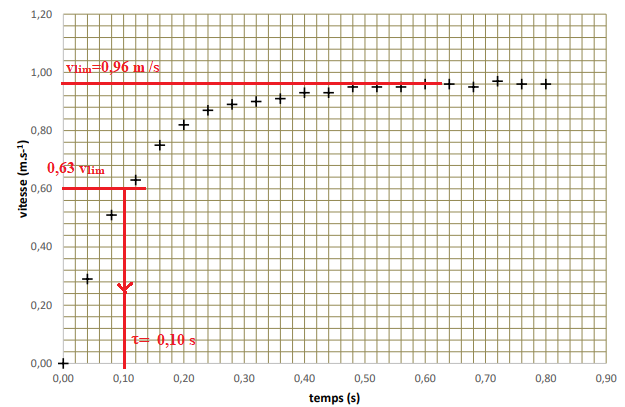
On filme, à l’aide d’une webcam réglée à 50 images par seconde,
la chute d’une bille d’acier dans l’huile d’olive contenue dans une
éprouvette graduée. La bille est lâchée sans vitesse initiale par
un électroaimant dans le référentiel terrestre supposé galiléen.
La vidéo est ensuite analysée image par image à l’aide d’un
logiciel approprié qui permet de repérer la position instantanée
du centre G de la bille suivant un axe (Oy) vertical orienté vers
le bas.
La vitesse instantanée à un instant ti est alors approchée par la
vitesse moyenne entre les instants ti et ti+1. L’évolution, au
cours du temps, de la valeur expérimentale de la vitesse v de la
bille est représentée.
Données : Masse de la bille : m = 4,1 g ; Rayon de la bille : R = 5,0 mm.
Masse volumique de l’huile à 20 °C : rhuile= 920 kg·m-3 . Viscosité de l’huile à 20°C : h = 0,39 Pa·s.
1. Déterminer graphiquement, en ajoutant les traits de construction utiles la valeur de la vitesse limite vlim atteinte par la bille ; le temps caractéristique t d’évolution de la vitesse.
Étude théorique du mouvement de la bille.
On étudie le mouvement du système « bille », plongée dans l’huile, dans le référentiel
terrestre supposé galiléen. Lors de sa chute, la bille est soumise à plusieurs actions
mécaniques :
- son poids P ;
- la poussée d’Archimède, notée P , de sens contraire à celui du poids et d’expression P= rhuile · V · g où rhuile est la masse volumique de l’huile en kg·m-3
, V le
volume immergé de l’objet en m3 et 𝑔 l’intensité de la pesanteur en m·s
-2
;
- la force de frottement f de l’huile sur la bille, que l’on suppose ici proportionnelle à
la vitesse de chute de la bille avec
f = 6pRh v où h est la viscosité de l’huile
en Pa·s, 𝑅 le rayon de la bille en m et v la vitesse de la bille en m·s
-1
.
2. Écrire l’expression vectorielle de la seconde loi de Newton appliquée au système
« bille ».
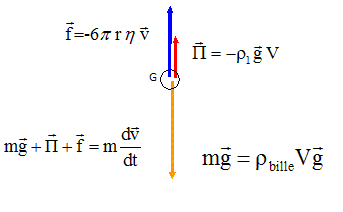3. Par projection de l’expression vectorielle de la seconde loi de Newton sur l’axe (Oy),
établir l’équation différentielle vérifiée par la vitesse v de la bille. Écrire cette équation
différentielle sous la forme dv /dt
= A v +B et exprimer les coefficients 𝐴 et 𝐵 en fonction des données.
mg -rhuileVg -6pRhv = mdv /dt.
dv /dt +6pRh / m v = g -rhuileVg / m.
A =6pRh / m ; B =g -rhuileVg / m.
4. À l’aide des données, poser explicitement les calculs qui permettraient de déterminer
la valeur numérique du coefficient A en s
-1 et celle du coefficient B en m·s
-2
.
A = 6 x3,14 x 5 10-3 x0,39 / (4,1 10-3)~9,0 s-1.
B =9,8 [1-920 x4 / 3 x3,14 x(5 10-3)3 / (4,1 10-3)=8,6.
Pour établir l’expression de la vitesse de la bille, les données physiques de l’expérience
conduisent à résoudre l’équation différentielle (E) : y’ = − 9 y + 8,6.
5. Déterminer la fonction solution de l’équation différentielle (E) s’annulant en 0.
Solution générale de y'+9y=0 : y = A exp(-9t).
Solurion particulière de (E) : y = 8,6 /9 =0,96 ( vitesse limite ).
Solution générale de (E) : y = A exp(-9t) +0,96.
A t = 0, y = 0 soit 0 = A+0,96 ; A = -0,96.
y = 0,96 (1-exp(-9t).
6. Montrer que la limite de 0,96 (1 –exp(-9t)
) lorsque 𝑡 tend vers +∞ est égale à 0,96.
Le terme en exponentielle tend vers zéro si t devient très grand et la vitesse tend vers 0,96 m /s.
7. Expliquer en quoi la comparaison de la valeur obtenue à la question 6 aux résultats de
l’étude expérimentale fournit un argument en faveur du choix du modèle des forces de
frottement fluide effectué en début d’exercice.
Les valeurs de la vitesse limite étant identiques, le choix du modèle des forces de
frottement fluide est correct.
|
...
|
....
|
Premier navire à hydrogène
Energy Observer est le premier navire à hydrogène autonome en énergie, sans émission
de gaz à effet de serre ou de particules fines. Ce navire du futur à propulsion fonctionne
avec trois sources d'énergie renouvelables (solaire, éolien et hydrolien) et deux formes
de stockage d’énergie (batteries pour le court terme et dihydrogène pour le long terme).
Durant la journée, la propulsion du bateau est assurée grâce à l’énergie solaire. Dès que
la nuit tombe et que les batteries atteignent environ 20 % de leur capacité, la pile à
combustible démarre automatiquement afin de remonter leur niveau de charge. Cette
opération peut être réalisée en moins de deux heures. Ainsi, la vitesse peut être
maintenue et les pics de consommation nocturnes respectés (repas, vie à bord, envois
de données, eau chaude produite avec la chaleur de la pile).
Huit réservoirs de 332 L permettent de stocker un total de 63 kg de dihydrogène, soit
l’équivalent en énergie de 230 L d’essence. Ce volume total représente une énergie nette
stockée de 1,0 MWh.
Source : d’après https://www.reussir.fr/machinisme/la-pile-combustible-pour-sassurer-contre-les-microcoupures-delectricite
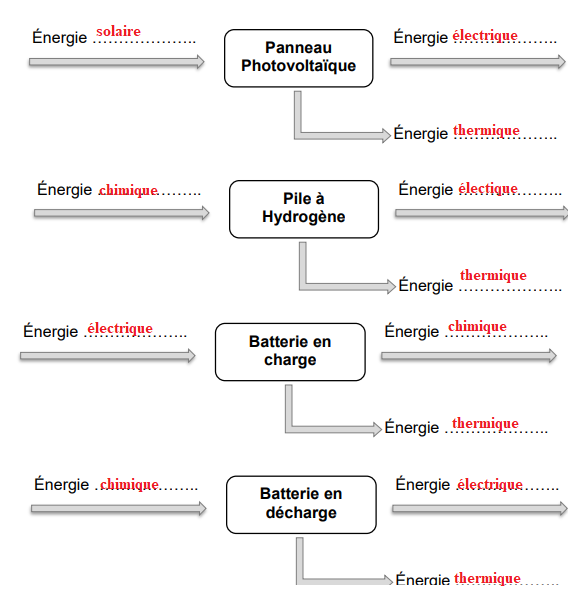
1. Compléter le schéma, en
faisant figurer les formes d’énergie qui interviennent.
2. Écrire les équations des réactions électrochimiques ayant lieu à chacune des
électrodes. Préciser pour chacune d’elles s’il s’agit d’une oxydation ou d’une réduction.
Réduction à la cathode positive : ½O2(g) +2H+ + 2e- --> H2O(l)
Oxydation à l'anode négative : H2(g) --> 2H+aq + 2e-.
3. En déduire l’équation de la réaction d’oxydo-réduction modélisant le fonctionnement de
la pile à hydrogène.
Additionner puis simplifier : ½O2(g) +H2(g) --> H2O(l)
4. Expliquer en quoi cette pile est considérée comme non polluante.
Le seul produit est l'eau et le comburant est le dioxygène de l'air.
5. Calculer la quantité de matière de dihydrogène disponible sur Energy Observer lorsque
les réservoirs sont pleins.
n = m / M(H2) = 63 103 /2 =3,15 104 mol.
6. En déduire l’énergie chimique disponible en J puis en Wh.
Énergie chimique libérée par une mole de dihydrogène lors du fonctionnement
de la pile à hydrogène : E = 2,4 × 105 J.
Energie disponible =2,4 105 x3,15 104 =7,6 109 J ou 7,6 109 / 3600 =2,1 106 Wh.
7. Le rendement de la pile étant égal à 46 %, calculer la quantité d’énergie électrique
disponible pour recharger les batteries. Montrer que ce résultat est cohérent avec les
indications du texte de présentation.
2,1 106 x 0,46 =9,7 105 Wh ~1 MWh.( en accord avec le texte).
.
Lors de la traversée Nassau (Bahamas) - Fort de France (Martinique) du 15 au 28 juillet
2020, la pile à hydrogène a fourni une puissance moyenne électrique de 30 kW. La durée
totale d’utilisation de la pile au cours de la traversée a été de 24 h. L’énergie électrique
totale pouvant être délivrée par cette pile était de 1,0 MWh.
On considèrera dans cette question la pile comme un générateur idéal de tension.
8. Définir ce qu’est un générateur idéal de tension.
La tension aux bornes d'un tel générateur est constante quelle que soit la charge.
9. Calculer l’énergie électrique délivrée par la pile au cours de la traversée.
10. Montrer que l’autonomie de la pile était suffisante pour cette traversée.
Energie (kWh) =puissance (kW) x durée (heure) =30 x 24=7,2 102 kWh, valeur inférieure à 1MWh.
|
|