Sauver
Venise et son patrimoine, bac SPCL Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Restauration de la lagune. 8 points
La lagune est une des richesses de Venise. Il s’agit d’une étendue d’eau de 550 km2
séparée de la mer Adriatique par un cordon littoral. Environ 8% de la
surface de la lagune sont occupés par Venise et de nombreuses petites
îles.
La lagune de Venise a subi de nombreuses interventions humaines qui ont
conduit à l’augmentation de la salinité de l’eau et à la réduction de
la surface occupée par les roseaux (la cannaie), habitat précieux pour
des espèces vivantes protégées ou d’intérêt commercial (oiseaux,
poissons). Le projet « Life Lagoon Refresh » vise à recréer cet habitat
perdu avec le temps. Mais la cannaie exige une valeur de salinité
inférieure à 15. Celle-ci est proche de 30 au coeur de la lagune, soit
une valeur très proche de celle de la mer (35 en moyenne).
Le projet « Life Lagoon Refresh » vise à faire baisser la valeur de la
salinité dans la lagune, en y injectant l'eau douce du fleuve Sile
quand cela est nécessaire. Un petit canal, opérationnel depuis mai
2020, permet une modulation du débit de l'eau en fonction de l'avancée
du projet ou d'événements comme les grandes marées.
D’après www.sciencesetavenir.fr, août 2020.
Cette partie s’intéresse à la détermination de la salinité d’un échantillon d’eau de la lagune de Venise.
La salinité désigne la concentration en masse de sels (composés
ioniques) dissous dans l’eau liquide. Elle est exprimée en gramme de
sels dissous par kilogramme d’eau, mais la valeur est notée sans unité.
Ainsi la salinité moyenne de l’eau de mer vaut 35, ce qui signifie 35 g
de sels dissous par kilogramme d’eau.
Actuellement, dans les laboratoires, la mesure de la salinité est
réalisée par conductimétrie. Une autre méthode, utilisée auparavant,
consiste en un titrage colorimétrique des ions halogénures (Cl−, Br−, etc.). Celle-ci sera employée ici.
En effet les proportions des constituants principaux de l’eau de mer
sont quasiment constantes. Le seul dosage de l’un d’entre eux permet
donc de déduire la concentration de tous les autres, et une valeur de
la salinité. La relation entre la salinité S et la chlorinité Ch a été
définie en 1902 à partir des analyses de nombreux échantillons
provenant de toutes les mers du monde. La chloronité caractérise la
quantité d’ions halogénure (Cl−, Br−, etc.) dans
l’eau ; elle est exprimée en masse équivalente d’ions chlorure par
kilogramme d’eau. La relation entre la salinité et la chloronité est la
suivante :
𝑆 = 0,030 + 1,805 × Ch.
On suppose que cette relation est valable pour l’eau de la lagune, dont
la composition est considérée comme proche de celle d’une eau de mer.
On réalise un titrage direct des ions halogénure par les ions argent Ag+. On note X– les ions halogénures (Cl−, Br −, etc.). L’équation de la réaction de titrage des ions halogénure est la suivante :
X–(aq) + Ag+(aq) → AgX(s)
À partir du prélèvement de l’eau de la lagune, noté (A), on prépare une
solution diluée au 1/20ème pour réaliser le titrage. La solution diluée
est notée (B).
Q1 - Donner le
protocole expérimental permettant de préparer 200 mL de la solution
diluée (B), en précisant les caractéristiques de la verrerie utilisée.
Prélever 200 / 20 = 10,0 mL de solution mère à l'aide d'une pipette jaugée de 10,0 mL.
Verser dans une fiole jaugée de 200 mL contenant un tiers d'eau distillée. Agiter.
Compléter jusqu'au trait de jauge à l'aide d'eau distillée.
Agiter pour rendre homogène.
Dans un erlenmeyer de 100 mL, on introduit un volume VB = 50,0 mL de la solution (B). On ajoute un volume V1 = 2 mL d’une solution aqueuse de chromate de potassium (2K+(aq) + CrO42–(aq)), de concentration C1 = 0,2 mol·L−1 : il s’agit de l’indicateur de fin de titrage. Sous agitation magnétique, on titre la solution par du nitrate d’argent (Ag+(aq) + NO3–(aq)) de concentration C0 = 0,100 mol·L−1. L’équivalence est atteinte lorsqu’apparait la coloration orange de l’indicateur et que cette coloration persiste 30 s.
Q2 - En utilisant les données issues des fiches de sécurité, indiquer les précautions nécessaires pour réaliser le titrage.
Port de blouse, gants et lunette de protection ; ne rien jeter à l'évier.
Q3 - Indiquer quel est l’élément de verrerie à utiliser pour prélever le volume VB. Même question pour le volume V1. Justifier.
VB est précis, donc prélever à l'aide d'une pipette jaugée.
V1 est peu précis, prélever à l'aide d'une pipette graduée.
Q4 - Réaliser le schéma légendé du montage utilisé lors du titrage.
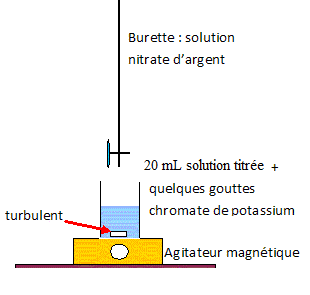
Le volume versé à l’équivalence est VE = 11,20 mL.
Q5 - Définir l’équivalence lors d’un titrage.
A l'équivalence, les quantités de matière des réactifs sont en proportions stoechiométriques. Avant l'équivalence X- est en excès ; après l'équivalence Ag+ est en excès.
Q6 - Déterminer la valeur de la concentration molaire (ou concentration en quantité de matière) CB en ions halogénure X− dans la solution diluée (B).
CB VB = C0 VE à l'équivalence.
CB = C0 VE / VB= 0,100 x 11,20 / 50,0 =2,24 10-2 mol / L.
On cherche à évaluer l’incertitude-type sur la concentration CB.
L’incertitude-type u(VB) sur la prise d’essai de solution (B) est de 0,05 mL. On estime que l’incertitude-type u(VE) sur la détermination du volume équivalent VE vaut 0,05 mL.
On estime que l’incertitude-type u(C0) sur la concentration de la solution de nitrate d’argent est u(C0) = 0,001 mol / L.
Q7 - Calculer u(CB) puis exprimer le résultat de la mesure avec le nombre de chiffres significatifs adapté.
u(CB) = CB [(u(VB) / VB)2+(u(C0) / C0)2+(u(VE) / VE)2+]½ =CB [(0,05) / 50)2+(0,001 / 0,1)2+(0,05) / 11,2)2+]½ .
u(CB) =2,24 10-2 x [1x 10-6 +1 x10-4 +2 x10-5]½ =2,24 10-2 x1,1 10-2 =2,5 10-4 mol / L.
CB = (224 ±3) 10-4 mol / L.
Q8 - Calculer la valeur de la concentration molaire CA en ions halogénure de l’échantillon d’eau de la lagune de Venise.
Tenir compte de la dilution au 20ème : CA=20 x 2,24 10-2=0,448 ~0,45 mol / L.
Par définition, la chloronité Ch est exprimée en masse équivalente d’ions chlorure par kilogramme d’eau.
On suppose que la masse volumique de l’eau salée est approximativement égale à 1,03 kg / L.
Q9 - À partir de la définition de la chloronité Ch et en considérant
que la concentration en quantité de matière en ions chlorure est égale
à CA, montrer que la chloronité Ch vaut 15,4 g par kilogramme d’eau.
0,448 x M(Cl-) =0,448 x35,5 = 15,9 g / L.
Ch=15,9 / 1,03 ~15,4 g par kilogramme d’eau.
Q10 - En déduire la valeur de la salinité S de l’eau de la lagune au moment du prélèvement.
𝑆 = 0,030 + 1,805 × Ch = 0,030 + 1,805 x15,4 =27,9 masse équivalente d’ions chlorure par
kilogramme d’eau.
Q11 - Conclure sur les conditions de développement de la cannaie.
La cannaie exige une valeur de salinité
inférieure à 15. Elle ne peut donc pas se développer.
Exercice 2. 12
points.
Prévision et lutte contre l’aqua alta de Venise avec le projet MOSE (6 points)
Mots-clés : débit, principe fondamental de la statique des fluides, puissance hydraulique, échangeurs et transferts thermiques.
Données
Accélération de pesanteur g = 9,81 m s–2.
Masse volumique de l’eau à 20°C : reau = 1,0 103 kg·m–3.
On suppose que la valeur de la pression atmosphérique est : P0 = 105 Pa = 1 bar.
Le système MOSE est un système intégré de défense formé de rangées de vannes mobiles escamotables.
Il permet d’isoler la lagune de Venise de la mer Adriatique durant les
phénomènes de hautes marées dépassant un niveau établi (110 cm) et
jusqu’à un niveau maximum de 3 mètres.
Cet ouvrage devrait permettre de défendre Venise contre les phénomènes
extrêmes comme les inondations (« acqua alta ») et éviter sa
dégradation morphologique, qui provoque l’envahissement progressif de
la lagune par la mer et l’affaissement du sol.
La réalisation du projet a démarré en 2003 dans les trois passes du
Lido, de Malamocco et de Chioggia, qui mettent en communication la
lagune et la mer. La totalité des ouvrages est opérationnel depuis le 3
octobre 2020.
En cas de prévision d’une marée supérieure à 110 cm, les vannes sont
vidées de leur eau par injection d’air comprimé et se soulèvent,
pivotant autour de l’axe de leurs charnières jusqu’à émerger de l’eau
et isoler la lagune de la mer en empêchant le passage du flux de la
marée.
Les 78 vannes mobiles sont réparties en quatre tronçons sur les trois
entrées de la lagune. Elles sont installées à une profondeur h1 = 20 m sous le niveau de la mer.
On considère que chaque vanne peut être modélisée par un caisson de
largeur L = 20 m, de hauteur H = 28 m et d’épaisseur de l’ordre de e =
2 m.
Q12 - Déterminer la valeur du débit volumique de l’air DV nécessaire pour que la levée d’une vanne suite à l’injection d’air comprimé prenne moins qu’une heure.
Volume du caisson : 20 x 28 x2 =1,12 103 m3.
Débit volumique d'air : DV = 1,12 103 / 3600 =0,31 m3 / s.
Q13 - Sachant que
la pression de l’air comprimé doit être supérieure à celle de l’eau
dans le caisson de la vanne, montrer que la valeur de la pression seuil
d’air comprimé Pseuil à appliquer pour que l’eau soit chassée du caisson et qu’il se soulève est d’environ 3 bar.
Pression de l'eau à une profondeur de 20 m : Pseuil = reau g h + P0 = 1,0 103 x 9,81 x 20 + 105 =2,96 105 Pa ~ 3 bar.
Q14 - Donner la définition de la puissance utile Pu d’une pompe.
La puissance utile (watt) est égale au produit d'une pression (Pa)(
différence de pression entre le fond et la surface ) par le débit
volumique ( m3 / s).
Q15 - Montrer que la puissance utile Pu min minimale de la pompe permettant le soulèvement d’un caisson doit avoir une valeur approximative Pu min = 62 kW.
DV reau g h =0,31 x 1,0 103 x 9,81 x 20 =6,1 104 W = 61 kW.
Q16 - Commenter la valeur de la puissance utile nécessaire au soulèvement de toute la digue.
Nombre de vanne x Pu min = 78 x 62 =4,8 103 kW = 4,8 MW, du même ordre de grandeur que la puissance de sortie mécanique d'un TGV duplex alimenté en 25 kV alternatif.
À la sortie du compresseur, l’air comprimé est à une température trop
élevée pour pouvoir être directement injecté dans les caissons qui sont
construits en acier traité pour résister à la corrosion dans un milieu
très agressif comme l'eau de mer salée.
L'air comprimé chaud sort du compresseur à vis à la température T1 = 100°C. Il est ensuite refroidi dans un échangeur thermique à faisceau tubulaire, avant stockage dans un réservoir.
On considère que l’air comprimé chaud est sec et que sa capacité thermique massique à pression constante a une valeur cair = 1,00 kJ kg–1·K–1.
En première approximation, on suppose que la masse volumique de l’air
comprimé reste constante pendant le refroidissement et que sa valeur
est égale rac = 3,3 kg m–3.
Q17 - Décrire qualitativement le principe d’un échangeur thermique.
Un échangeur thermique ne mélange pas les fluides, il permet le transfert de chaleur entre deux fluides au travers d'une paroi.
Q18 - Donner la relation entre débit massique et débit volumique.
Débit volumique ( m3 /s) x masse volumique du fluide ( kg m-3) = débit massique ( kg /s).
Q19 - Calculer la valeur du débit massique de l’air comprimé dans le cas où la valeur du débit volumique de l’air est DV = 0,50 m3s–1.
DV rac =0,50 x 3,3 =1,65 kg / s.
Q20 - Estimer la valeur de la puissance thermique à absorber pour refroidir l’air comprimé jusqu’à la température ambiante Tamb = 15 °C.
Débit massique x Cair x différence de température =1,95 x1,00 x (100-15) =165,75 ~166 kW.
|
...
|
....
|
Partie B. Mesure de l’évolution du niveau de la mer (6 points)
Mots-clés : ondes progressives périodiques, diffraction des ondes.
Donnée
Vitesse de la lumière dans le vide : c = 2,99794×108 m s–1.
L’altimètre Poséidon est un radar embarqué sur le satellite émettant
verticalement (visée nadir) des ondes radios, sous forme de brèves
impulsions. Les ondes se réfléchissent sur la surface des océans.
L'écho de chaque impulsion est détecté et analysé à bord du satellite,
ce qui conduit à une détermination précise de la distance «
altimétrique » : Ha, entre le satellite et le niveau de la mer
connaissant la durée Dt d'aller-retour du signal radar et la célérité V de propagation de l'onde.
Q21 - Indiquer si une onde électromagnétique est une onde longitudinale ou une onde transversale.
Une onde électromagnétique est une onde transversale ; seule les ondes mécaniques peuvent être longitudinale.
Q22 - Exprimer la longueur d’onde l de l'onde émise par le radar embarqué sur le satellite puis calculer sa valeur pour la fréquence 13,576 GHz.
l = c / f = 2,99794×108 / (13,576 109) =2,2083 10-2 m.
Q23 - Préciser le domaine spectral de cette onde et justifier le choix de ce domaine.
Les ondes radio ne sont pas absorbées, bloquées, par l'atmosphère terrestre.
Q24 - Exprimer la distance « altimétrique » Ha en fonction de la célérité V de l’onde du radar, et de la durée Dt d’un aller-retour.
Ha = V Dt / 2.
La vitesse de propagation de l’onde dépend de la composition de
l’atmosphère, ainsi l’indice de réfraction du milieu peut varier entre
1,00029 et 1,00032.
Q25 - Est-il
nécessaire de disposer d’un système afin d’évaluer l’impact de cet
indice sachant que la position du satellite doit être déterminée au
centimètre près ? Justifier la réponse à l’aide d’applications
numériques et en faisant preuve d’esprit critique.
Donnée : durée d’un aller-retour : Dt = 8,91283 ms.
Vmini = c / n = 2,99794×108 / 1,00032=2,996981 108 m /s.
Ha mini = V Dt / 2 =2,996981 108 x 8,91283 10-3 / 2 =1,33558 106 m
Vmaxi = c / n = 2,99794×108 / 1,00029=2,997071 108 m /s.
Ha maxii = V Dt / 2 =2,997071 108 x 8,91283 10-3 / 2 =1,33562 106 m.
Différence des deux altitudes : 39 m.
Il est nécessaire de disposer d’un système afin d’évaluer l’impact de cet indice.
L’onde émise par le radar subit un élargissement caractérisé par une ouverture angulaire « q » représentée sur le document ci-dessous.
La zone étudiée à la surface de la mer est alors un disque caractérisé par un rayon R.
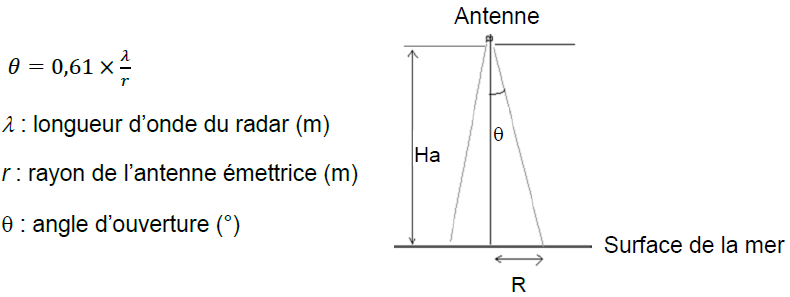
On admet que la valeur de l’altitude du satellite est Ha = 1 336 km et que la valeur de la longueur d’onde émise est l = 2,2 cm.
Q26 - Expliquer pourquoi le faisceau de l’onde électromagnétique est élargi.
Diffraction par une ouverture très petite.
Q27 - En considérant que tan(q) est peu différent de q (en radian), établir une relation entre R, Ha, r et l.
tan q ~q =R / Ha.
De plus q = 0,61 l / r.
0,61 l / r = R / Ha. R = 0,61 l Ha / r.
Q28 - Calculer la
valeur du rayon R de la surface au sol couverte par le faisceau LASER.
Comparer à la résolution (points sous le satellite) précisée dans le
tableau ci-dessus de JASON-2.
r = 0,60 m.
R = 0,61 x0,022 x 1,336 103 / 0,60=29,9 ~ 30 km, valeur identique à la résolution points sous le satellite.
Composition chimique du vernis d’un tableau (6 points)
Mots-clés : spectroscopie infrarouge, activité optique, stéréochimie, distillation.
On fait l’hypothèse que le tableau de l'artiste utilise comme liant un mélange d'huile de lin et de térébenthine de Venise :
- l’huile de lin est constituée en particulier d’acides gras (acides
carboxyliques à longues chaînes carbonées) et de triglycérides (esters)
;
- la térébenthine de Venise est obtenue par distillation de la résine
de certains arbres (mélèzes, pins). Elle contient des terpènes,
c’est-à-dire des hydrocarbures présentant une ou plusieurs liaisons
doubles carbone-carbone.
La composition chimique du vernis est étudiée après prélèvement d’une
fibre du tableau et analyse par différentes techniques
spectroscopiques. Un spectre infrarouge (FTIR) obtenu lors de l’analyse
du vernis sur cette fibre, est donné ci-après.
Q29 - En exploitant
le spectre infrarouge précédent, discuter de la validité de l’hypothèse
réalisée sur la composition chimique du vernis (mélange d’huile de lin
et de térébenthine de Venise).
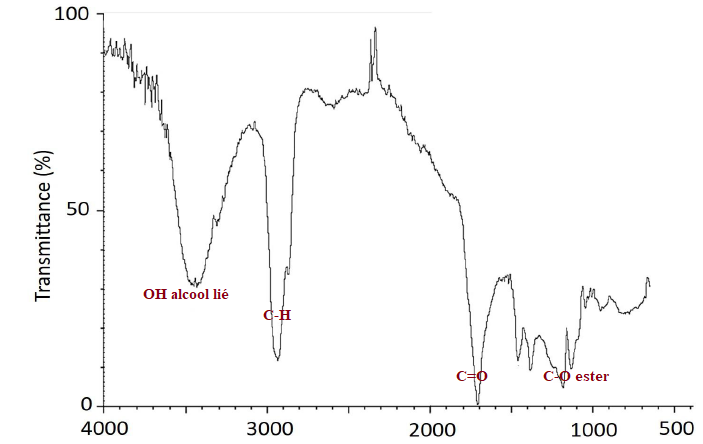
Absence de la bande caractéristique de la liaison C=C vers 1620 - 1700 cm-1. L'hypothèse n'est pas valide.
Parmi les espèces chimiques présentes dans la térébenthine de Venise,
on trouve de l’α-pinène, un terpène présent sous la forme de deux
stéréoisomères : le (-)-α-pinène et le (+)-α-pinène et dont les
structures sont indiquées ci-dessous :
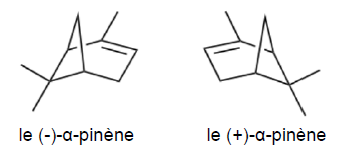
Q30 - Indiquer si
la relation de stéréoisomérie entre ces deux molécules, est une
énantiomérie ou une diastéréoisomérie. Justifier la réponse.
Les deux molécules sont images l'une de l'autre dans un miroir plan. Ce sont deux énantiomères.
On considère l’activité optique du (-)-α-pinène et du (+)-α-pinène.
Données : pouvoirs rotatoires spécifiques à 22°C
(−)-α-pinène : [α]D22 = – 51°·dm−1·L·g−1 ;
(+)-α-pinène : [α]D22 = + 51°·dm−1·L·g−1.
Q31 - Parmi les
propositions suivantes, identifier les propositions correctes. Indiquer
sur la copie les lettres associées aux propositions correctes, parmi a,
b, c et d.
a. L’activité optique du (+)-α-pinène est associée à la chiralité des molécules de (+)-α-pinène. Vrai.
b. L’activité
optique du (−)-α-pinène est associée à la présence d’une liaison double
carbone-carbone dans les molécules de cette espèce chimique. Faux.
c. La valeur du
pouvoir rotatoire du (+)-α-pinène est obtenue en mesurant l’angle de
réfraction de la lumière à l’interface entre l’air et le (+)-α-pinène
liquide. Faux .
d. Lorsqu’une
lumière polarisée rectilignement traverse une solution de (+)-α-pinène,
la direction de polarisation de cette lumière tourne d’un angle
correspondant au pouvoir rotatoire du (+)-α-pinène. Vrai.
L’a-pinène (sous
forme d’un mélange de (-)-α-pinène et de (+)-α-pinène) peut être
extrait par distillation fractionnée d’une huile de térébenthine de
pin. Les principaux terpènes constituant l’huile de térébenthine de pin
sont indiqués dans le tableau ci-après.
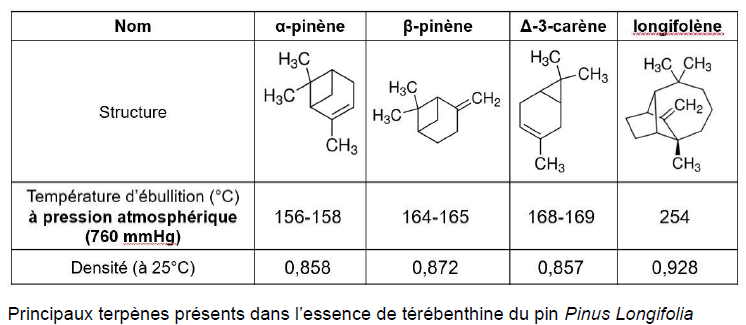
Q32 - À partir des
données disponibles, justifier qu’en début de distillation fractionnée,
l’α-pinène est présent en quantité très majoritaire dans le distillat.
L’α-pinène est l'espèce la plus volatile.
Q33 -
Justifier la nécessité de recourir à une distillation sous pression
réduite de 11 mmHg au lieu d’une distillation sous pression
atmosphérique 760 mmHg.
A température assez élevée ( 254 °C) certaines molécules peuvent être détruites.
Le schéma d’un montage de distillation sous pression réduite est donné ci-après.
Q34 - Légender ce schéma.
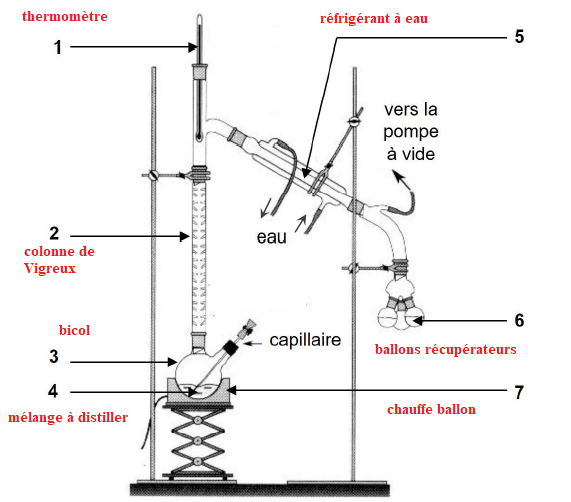
Le document ci-après rend compte de l’avancée de la distillation sous
une pression réduite de 11 mmHg : sur le graphique est représentée
l’évolution de paramètres physiques en fonction de la quantité d’huile
de térébenthine distillée.
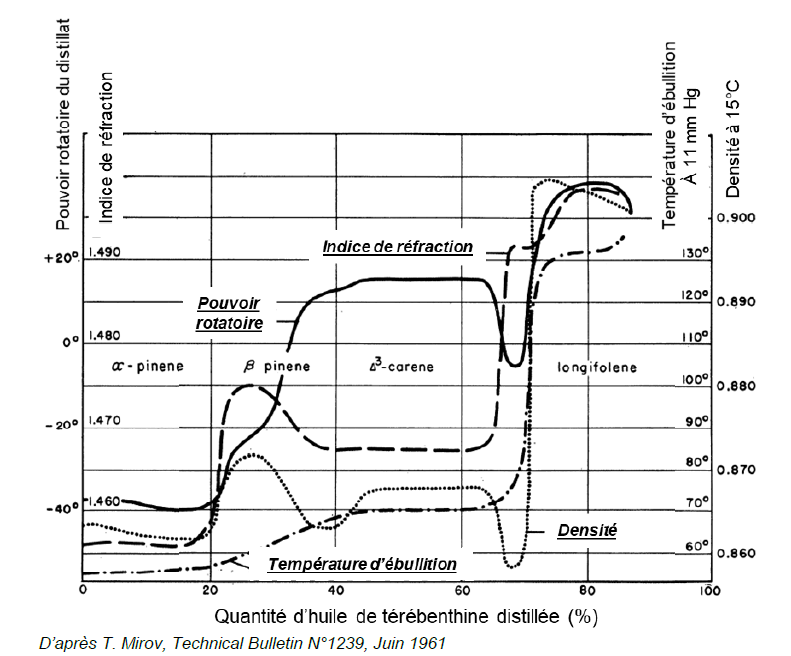
Q35 - Estimer
graphiquement la valeur du pouvoir rotatoire du distillat lorsque 20 %
de la quantité d’huile de térébenthine de pin est distillée.
Environ - 38 °.
Q36 - En déduire le nom du stéréoisomère de l’a-pinène qui est majoritaire dans le distillat obtenu.
(−)-α-pinène : [α]D22 = – 51°·dm−1·L·g−1 ;
|
|