Pour les questions 1 et 2, on considère la fonction suivante :
Soit 𝑔 la fonction définie sur l’intervalle [0 ; +oo[ par :
g(x) = (2x-1) e
-x.
1.
Calculer g(0).
g(0) = (2*0-1)e
-0 =-1 x1 = -1.
2. On admet que la fonction g est dérivable sur l’intervalle [0 ; +oo[ et on note g' sa fonction
dérivée.
2. a. Montrer que, pour tout réel x appartenant à [0 ; +oo[, g
′
(𝑥) = (−2x + 3)𝑒
−𝑥.
On pose u = 2x-1 et v = e
-x. u' = 2 ; v' = -e
-x.
g' (x) =u'v+v'u =2e
-x-(2x-1)e
-x = e
-x(2-2x+1) =
(−2x + 3)𝑒
−𝑥.
2. b. Justifier que g(x) < 2 e
-1,5 pour x >1,5.
g'(x) = 0 si x = 1,5.
g(1,5) = 2e-1,5.
g'(x) > 0 si x appartient à [0 ; 1,5 [ et g(x) est strictement croissante.
g'(x) < 0 si x appartient à ]1,5 ; +oo [ et g(x) est strictement décroissante de 2e-1,5 à zéro.
La fonction g(x) est continue car dérivable ; elle est strictement décroissante de 2e-1,5 à zéro sur ]1,5 ; +oo [.
Donc g(x) < 2 e-1,5 pour x >1,5.
3. Sachant que cos (9
p /5)=
(√5+1) /
4
, exprimer cos (
p/
5
) en fonction de √5.
9p /5 = 10 p / 5-p /5 = 2p-p /5.
cos (9p /5)= cos(2 p-p /5) = cos (-p /5) = cos(p /5).
cos (p /5)=
(√5+1) /
4.
4.
On considère l’intégrale I suivante :
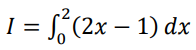
Montrer que I = 2.
Primitive de 2x-1 : F(x) = x
2-x.
I = F(2) -F(0) = 2
2-2-0 = 2.
5.Simplifier le nombre suivant en détaillant les calculs :
A = 5 ln(e
3)-4 ln(1 / e
2).
ln(e
3) = 3 ln(e) = 3.
ln(1 / e2)= -ln(e2) = -2 ln(e) = -2.
A = 5 *3-4*(-2) = 15 +8 =23.
6. ABCD est un carré de côté 3 cm et DCE est un triangle rectangle et isocèle en C.
Donner la valeur du produit scalaire suivant :
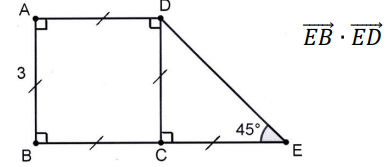
EB = 6 ; ED = 3 / sin 45 =3 x2
½.
Le produit scalaire vaut : EB x ED cos 45 =6 x3 x2
½ x 2
½ / 2 =18.
..