1. L'avion SolarStratos.
1.1. Donner deux contraintes au projet de vol de SolarStratos.
Atteindre l'altitude de 25 000 m. L’avion et son pilote seront soumis à des températures extrêmes, de l’ordre
de - 70°C. »
Minimiser le poids de l'appareil.
1.2. Compléter le document en indiquant les
différents transferts d’énergie mis en jeu dans la chaîne énergétique de propulsion de
l’avion.
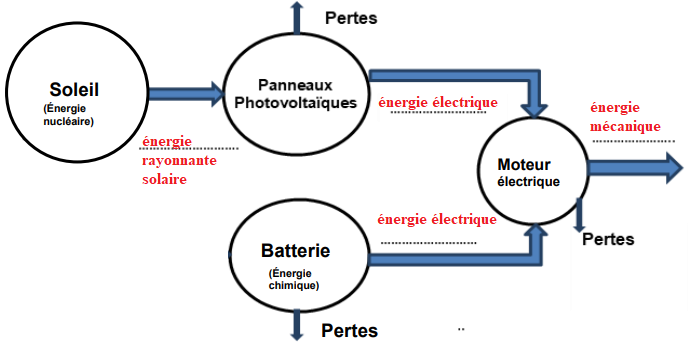 1.3.
1.3. Nommer la dissipation d’énergie correspondant aux pertes se produisant au niveau du
moteur. Préciser à quel phénomène physique sont dues ces pertes.
Energie thermique dissipée lors des frottements mécaniques.
1.4. Déterminer la puissance solaire moyenne P
Sol reçue par l’ensemble des panneaux
photovoltaïques.
Surface des panneaux S = 22 m
2.
Eclairement solaire moyen : 1200 W / m
2.
P
sol = 1200 x22 =26 400 W = 26,4 kW.
1.5. Donner l’expression du rendement
h d’un panneau solaire. Déterminer la valeur de la
puissance électrique P
PV fournie par l’ensemble des panneaux photovoltaïques au
moteur.
Rendement = puissance électrique fournie / puissance solaire reçue.
P
PV = P
sol x rendement =26,4 x0,24 =6,3 kW.
1.6. Vérifier que la valeur de l’énergie E
PV fournie par les panneaux photovoltaïques lors de
la phase d’ascension et de maintien dans la stratosphère est égale à 17 kWh.
Durée du vol : 2 h 45 min soit 2,75 h..
EPV=
PPV x durée = 6,3 x2,75 =17,3 ~ 17 kWh.
1.7. Pour effectuer la mission, une énergie totale E
moteur dont la valeur est égale à 77 kWh
doit être fournie au moteur. En déduire la valeur de l’énergie E
batterie fournie par les
batteries lithium-ion.
E
batterie =
Emoteur -EPV=77 -17 = 60 kWh.
2. L’avion en vitesse de croisière dans la stratosphère
Dans cette partie, l’avion se déplace dans la stratosphère en ligne droite, à vitesse constante.
La portance et la trainée sont des actions mécaniques exercées par l’air sur les ailes de l’avion.
La traction, action générée par l’air du fait de la rotation des pales de l’hélice, permet à l’avion
de se déplacer. Les forces modélisant les actions mécaniques s’exerçant sur l’avion sont
représentées ci-dessous :
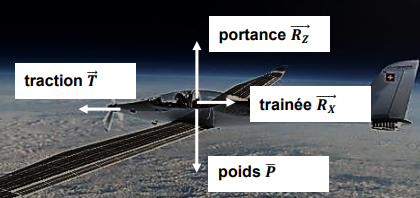
Données : Intensité de la pesanteur à 25 000 m d’altitude : g = 9,7 N.kg
-1 .
Masse volumique de l'air à 25 000 m d’altitude :
r = 7,0×10
-2 kg.m
-3 .
Vitesse de croisière de l’avion : v = 250 km.h
-1 = 69,4 m.s
-1 .
Surface totale des ailes de l’avion : S.
Expression de la force modélisant la portance : R
Z =0,5
r C
z v
2 S avec C
z = 1,1.
Expression de la force modélisant la trainée :
RX =0,5 r Cx v2 S avec Cx = 0,02.
2.1. Qualifier, en le justifiant, le mouvement de l’avion lorsque celui-ci se maintient dans la
stratosphère, à sa vitesse de croisière.
Mouvement rectiligne uniforme : l’avion se déplace dans la stratosphère en ligne droite, à vitesse constante.
2.2. Énoncer la seconde loi de Newton.
Dans un référentiel galiléen, la somme vectotielle des force
extérieures appliquées au système est égal au produit de la masse du
système par le vecteur accélération.
2.3. Appliquer la seconde loi de Newton à l’avion en vitesse de croisière et déterminer les
relations entre les forces de direction verticale, ainsi que les relations entre celles de
direction horizontale. En déduire quelle doit être la valeur de la surface S des ailes de
l’avion pour que ce mouvement dans la stratosphère puisse avoir lieu.
Mouvement rectiligne uniforme : les forces se compensent.
La traction Tcompense la trainée Rx.
La portance R
z compense le poids.
Masse de l'avion 450 kg ; poids = 450 x9,7 =4365 N.
Portance Rz =0,5 r Cz v2 S =0,5 x 0,07 x1,1 x69,42 S =138,57 S.
S = 4365 / 138,57 =25,9 ~26 m2.
2.4. Indiquer, en expliquant la réponse, si la surface S des ailes de l’avion SolarStratos est
suffisante pour accueillir les panneaux photovoltaïques nécessaires au
fonctionnement de l’avion.
Surface des panneaux : 22 m
2 < 26 m
2 ; la surface des ailes est suffisante.
..