Pouvoir virucide d’une eau de Javel.
L’eau de Javel est une solution aqueuse contenant des ions
hypochlorite ClO
–
(aq) et des ions
chlorure Cl
–
(aq) en quantité égale. L’ion hypochlorite lui confère des propriétés
désinfectantes
et virucides. En avril 2020, en lien avec l’épidémie de coronavirus,
l’Institut Pasteur de Lille
conseillait de nettoyer et de désinfecter le mobilier sanitaire avec
une solution d’eau de Javel
contenant une concentration minimale en ions hypochlorite C
min
égale à
0,076 mol.L
–1
.
Données :
Couples oxydant-réducteur : ClO
–
(aq) / Cl
–
(aq) ; O
2(g) / H
2O(l).
Une eau de Javel à 2,6% de chlore actif est telle que la
concentration initiale C
o en ions
hypochorite ClO
–
(aq) est C
o = 0,380 mol.L
–1
.
Dans une solution aqueuse d’eau de Javel, les ions hypochlorite se
décomposent. Cette
transformation chimique est lente et peut être modélisée par la
réaction d’équation :
ClO
–
(aq) --> ½ O
2(g) + Cl
–
(aq)
1. Donner
l’expression de la vitesse v(t) de la réaction de décomposition des
ions hypochlorite
dans laquelle C(t) est la concentration, à l’instant t, en ions
hypochlorite ClO
–
(aq) présents
dans la solution d’eau de Javel.
v(t) = - dC(t) / dt.
2. En faisant
l’hypothèse que la réaction admet un ordre 1 par rapport aux ions
hypochlorite
ClO
–
(aq), donner une autre expression de la vitesse de la réaction. On
introduira la
constante de vitesse k en précisant son unité.
v(t) = k [ClO
-aq]=k C(t) avec k en s
-1ou en jour
-1.
3. En déduire que la
concentration C(t) des ions hypochlorite ClO
–
(aq) vérifie : dC(t) / dt + k C(t) = 0.
v(t) = - dC(t)
/ dt = k C(t)
dC(t) /
dt + k C(t) = 0.
.
4. En déduire que,
dans le cadre de ce modèle, l’expression de la concentration C(t) est
donnée par C(t) =C
0 exp(-kt). Préciser ce que représente C
0.
Solution de l'équation différentielle C(t) = A exp(-kt) avec A une
constante.
A l'instant initial, C(t=0) = C
0 =A.
Par suite :
C(t) =C0
exp(-kt).
On réalise à présent une étude expérimentale de la cinétique de la
réaction de décomposition
des ions hypochlorite dans l’objectif de tester l’hypothèse de l’ordre
1.
À 20 °C, la concentration C(t) des ions hypochlorite ClO
–
(aq) contenus dans la solution
commerciale d’eau de Javel est suivie au cours du temps. Trois courbes
expérimentales sont
tracées et présentées ci-après (graphes 1,2 et 3).
5. Expliquer en quoi ces
résultats expérimentaux confirment l’ordre 1 de la réaction par rapport
aux ions hypochlorite ClO
–
(aq).
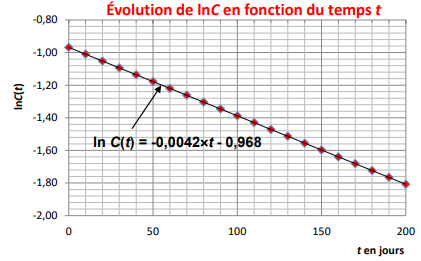ln C(t) =ln C0 -kt équation d'une droite
d'ordonnée à l'origine ln C0 = ln 0,38 = -0,968 et de
coefficient directeur -k = -0,0042 négatif.
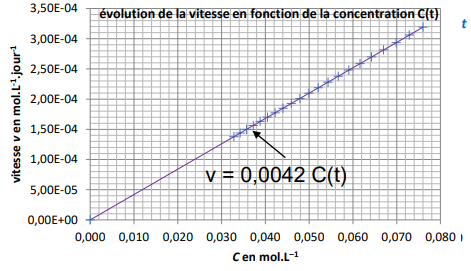
v(t) = k
C(t) ; la vitesse est
proportionnelle à la concentration C(t).
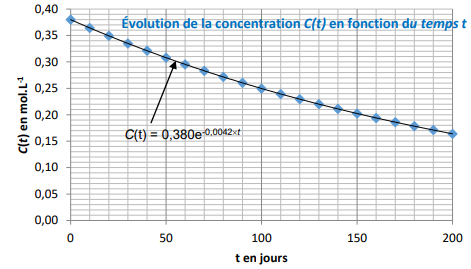
C(t) =0,38 exp(-kt),
le graphe est clui d'une exponentielle e-kt.
6. Déduire, des
résultats expérimentaux, la valeur k de la constante de vitesse de la
réaction
à 20 °C. Préciser son unité
k = 0,0042 jour
-1.
7. L’évolution
de la concentration en ions hypochlorite dans cette solution
commerciale est
donnée par la fonction C définie sur l’intervalle [0 ; 400] par C(t) =
0,380 exp(
−0,0042 t). Montrer, par le calcul, que la durée t pour laquelle une
eau de Javel à 2,6 % de chlore actif,
reste virucide, pour le coronavirus (conformément aux conseils
prodigués par l’Institut
Pasteur de Lille) est d’environ 380 jours.
C(t)> C
min
= 0,076 mol/L.
0,076
< -0,380
exp(-0,0042 t) ;
0,076 / 0,380
< -exp(-0,0042 t) ; 0,2 < - exp(-0,0042 t).
ln(0,2) < -0,0042
t ; -1,61 < -0,0042 t
t <1,61 / 0,0042 ;
t < 380 jours.
8. Porter un
regard critique sur les conseils d’utilisation figurant sur l’étiquette
de l’eau de Javel
à 2,6 % de chlore actif.
L'affirmation " à utiliser dans les trois ans suivant la date de
fabrication " est fausse.
