Electrophorèse,
pile à combustible, bac STL 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
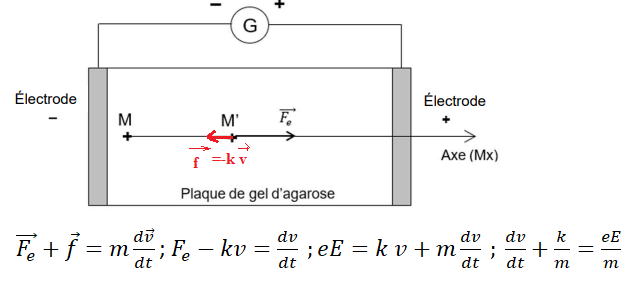
Une goutte d’un
mélange des deux acides aminés à séparer est déposée (point M de
la figure ci-dessous) sur une plaque horizontale recouverte de gel
d’agarose et
soumise à un champ électrostatique, dont la norme est notée E.
Les acides aminés, sous
forme anionique au pH imposé (ion aspartate et ion
glutamate), migrent vers l’électrode positive sous l’effet de la force
électrostatique,
notée Fe et représentée ci-dessus au point M’.
L’action du gel sur les molécules est modélisée par une force de
frottement f.
A.1. En justifiant la réponse dans
la copie, représenter , sans souci d’échelle, le vecteur force f
modélisant l’action du gel
sur les anions au point M’.
Le vecteur force f a le sens contraire du vecteur vitesse.
A.2. Écrire la seconde
loi de Newton pour un anion de masse m et l’appliquer dans le
cas de l’électrophorèse considérée.
A.3. Projeter la relation
vectorielle sur l’axe (Mx) et montrer que la valeur de la
vitesse v de migration de l’anion considéré est solution de l’équation
différentielle :
dv
dt
+
k/
m
× v =
e×E
/m.
PARTIE B – Étude du
mouvement de l’ion d’acide aspartique
Par application numérique, l’équation différentielle ci-dessus peut
s’écrire sous la
forme :
v'= − 1,3 ×1013v + 3,9×108 ,
(E)
où la vitesse v est exprimée en mètre par seconde (m·s–1) et
le temps t est exprimé
en seconde (s).
B.1. Déterminer la
solution générale 𝑣 de cette équation différentielle définie sur
[0 ; +∞[.
Solution générale de : v'+ 1,3 ×1013v
=0.
v = A exp(-1,3 1013t) avec A une constante.
Solution particulière de (E) : v = 3,9 108 /(1,3 1013)
=3,0 10-5 m /s.
Solution générale de (E) : v
= A exp(-1,3 1013t) +3,0 10-5.
B.2. Sachant que v (0) = 0, montrer
que, pour tout t ∈[0 ; +∞[,
v(t) = 3 10-5(1-exp(-1,3 1013t)).
v(t=0) = Ae0+3,0 10-5 =0 ; A = -3,0 10-5.
Par suite : v(t) = 3 10-5(1-exp(-1,3 1013t)).
B.3.
Justifier que la vitesse limite vaut 3 10-5 m /s.
Au bout d'un temps suffisamment grand, le terme en exponentielle est
nul.
vlim = 3 10-5 m /s.
.
B.4. On note t90 l’instant exprimé en seconde pour
lequel la vitesse atteint 90 % de
sa vitesse limite. Montrer que t90 = 1,8 ×10-13.
v(t90)
= 3 10-5(1-exp(-1,3 1013t90))=0,9
x3 10-5.
1-exp(-1,3 1013t90)=0,9.
exp(-1,3
1013t90)=0,1.
-1,3 1013t90
=ln(0,1)~ -2,3.
t90 ~1,8
10-13 s.
PARTIE C
– Détermination de la durée de migration.
Les résultats précédents montrent que le régime stationnaire est
atteint quasi
instantanément, si bien que l’on peut considérer que les constituants
du mélange se
déplacent suivant un mouvement rectiligne uniforme avec une vitesse
constante
égale à :
vlim=
e×E /
k
C.1. Comparer la
vitesse limite de migration des ions glutamate et des ions
aspartate.
e = 1,6 10-19 C ; E = 520 V / m ; kaspart = 2,7
10-12 N s m-1 ; kglutam
= 3,0 10-12 N s m-1 .
v lim aspart =1,6 10-19 x520 /(2,7 10-12)
=3,1 10-5 m /s.
v
lim glutam =1,6 10-19 x520 /(3 10-12)
=2,8 10-5 m /s.
En fin
d’électrophorèse, les taches sont révélées sous lumière ultraviolette.
On
admet qu’une différence de distance de migration d’au moins 5 mm est
nécessaire
pour distinguer la tache associée au mouvement des ions glutamate et
celle
associée au mouvement des ions aspartate.
C.2. Déterminer la
durée minimale de l’électrophorèse et les distances alors
parcourues par les ions pour pouvoir distinguer les deux taches
correctement.
Commenter les valeurs obtenues.
daspartam =
3,1 10-5 t ; dglutam = 2,8 10-5 t ;
daspartam
-dglutam > 5 10-3.
(3,1 -2,8) 10-5 t > 5 10-3.
t > 1,7 103
s. (28 min).
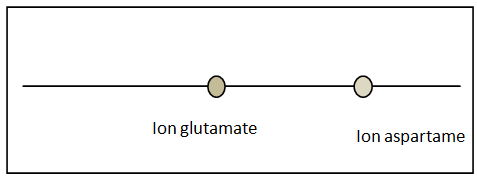
C.3.
Sur un schéma succinct de la plaque, positionner et identifier les
taches
obtenues après électrophorèse.
|
...
|
....
|
Générateur.
Partie
A : étude énergétique.
Une lampe de poche est alimentée par une pile plate modélisée par
un générateur,
de force électromotrice E = 4,7 V et de résistance interne r = 1,3 Ω.
L’intensité du
courant délivré par la pile est I = 0,31 A.
1. Calculer
l’énergie électrique, notée Eélec, reçue par la lampe si
elle est allumée
pendant deux minutes.
Eélec, = U I t.
U = E-rI =4,7 -1,3 x0,31 =4,297 V.
Eélec, =4,297 x0,31 x2 x60~1,6 102 J.
2. Calculer la valeur de
l’énergie, notée Ediss, dissipée par effet Joule à
l'intérieur de
la pile, pendant deux minutes.
Ediss = r I2 t =1,3 x 0,312 x120~ 15
J.
3. Identifier une
conséquence physique liée à l’existence d’une dissipation
d’énergie par effet Joule à l’intérieur de la pile.
Echaufement de la pile.
Partie B : détermination
expérimentale de la valeur de la résistance interne.
On se propose de déterminer expérimentalement
la valeur de la résistance interne d’une pile.
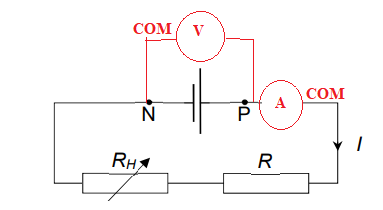
On réalise pour cela le montage suivant.
1. Reproduire le schéma
et le compléter en représentant les
appareils de mesure de la tension UPN aux bornes de la pile
et de l’intensité I du
courant électrique circulant dans le circuit. Préciser le sens de
branchement des
appareils en indiquant leurs bornes V, COM et mA.
2. Les
résultats des mesures effectuées sont données. Placer les points
expérimentaux.
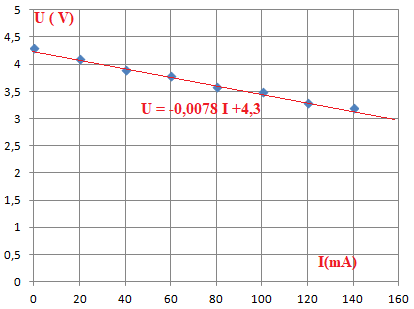
3. Déterminer
la valeur de la résistance interne r de la pile.
r = 0,0078 x 1000 = 7,8 ohms.
4. Selon le fabricant,
la valeur de la résistance interne de la pile est de 7,4 Ω.
Proposer une cause possible pour expliquer cette différence.
Ecart relatif : (7,8-7,4) / 7,4 ~0,054 (5,4 %.
Cet écart étant faible, erreur de lecture ou Imprécision sur les mesures de U et I.
Pile à combustible.
Une pile à combustible à méthanol direct (technologie DFMC) permet la
conversion
d’énergie chimique en énergie électrique.
Un réservoir de méthanol, appelé cartouche, fournit le combustible à la
pile et la
réaction du méthanol avec le dioxygène de l’air génère la circulation
du courant
électrique.
Cet exercice propose d’étudier les transformations chimiques ayant lieu
dans la pile
à combustible et envisage son utilisation pour recharger une batterie
de bateau.
Données : volume de méthanol contenu dans une cartouche : V = 5,0 L ; masse volumique du méthanol : r = 790 g L
-1 ; masse molaire moléculaire du méthanol : M = 32,0 g·mol-1 ; constante de Faraday : F = 9,65 104 C·mol-1
.
PARTIE A – Fonctionnement de la pile à combustible à méthanol direct.
Les réactifs de la pile à combustible sont le méthanol et le dioxygène
O2 de l’air.
La circulation d’ions H+ dans la membrane électrolytique permet
notamment le
maintien de l’électroneutralité à chaque électrode.
À l’électrode 1 se déroule l’oxydation du méthanol modélisée par la
demi-équation
électrochimique :
CH3−OH(l) + H2O(l) --> CO2(g) + 6 H+
(aq) + 6 e-
A.1. Justifier que le méthanol est un réducteur et écrire le couple
redox concerné.
Le méthanol cède des électrons, il est le réducteur du couple CO2(g) / CH3-OH(l).
A.2. Écrire la demi-équation électrochimique modélisant la
transformation chimique
qui se déroule à l’électrode 2 et fait intervenir le couple O2(g) /
H2O(l).
O2(g) + 4H+aq +4e---> 2H2O(l).
A.3. À partir des deux demi-équations électrochimiques, montrer que le
fonctionnement de la pile à combustible est modélisé par l’équation de
réaction :
2 CH3−OH(l) + 3 O2(g) --> 2 CO2(g) + 4 H2O(l)
2 fois [CH3−OH(l) + H2O(l) --> CO2(g) + 6 H+
(aq) + 6 e-
]
3 fois [O2(g) + 4H+aq +4e---> 2H2O(l)].
Additionner et simplifier.
A.4. Identifier, en justifiant la réponse,
l'anode et
la cathode et préciser leur polarité.
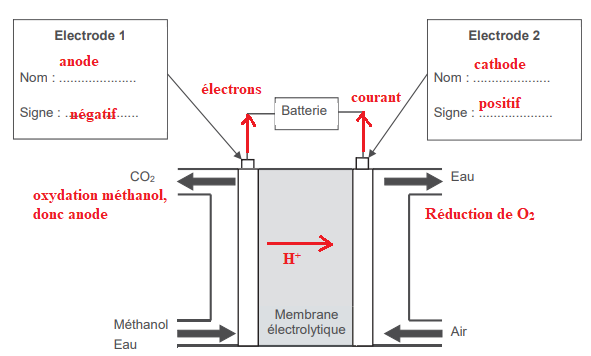
A.5.Indiquer les sens de circulation des
électrons et du courant électrique.
A.6. Indiquer le sens de circulation des
ions H+
dans la membrane.
PARTIE B – Autonomie de la pile à combustible
B.1. Montrer que la quantité de matière de méthanol contenue dans une
cartouche
est environ égale à nméthanol = 1,2 × 102 mol.
masse =5,0 x790 =3950 g.
nméthanol = mase / masse molaire = 3950 / 32,0 =1,2 102 mol.
B.2. En s’appuyant sur l’équation de demi-réaction électrochimique se
déroulant à
l’électrode 1, montrer que, lorsque la totalité du méthanol est
consommée, la quantité
de matière d’électrons échangée dans la pile est environ égale à ne
- = 7,2×102 mol.
ne
- = 6 nméthanol =6 x 1,2 × 102 =7,2×102 mol.
B.3. Déduire la quantité d’électricité Q que peut fournir la
consommation de la totalité
de la cartouche de méthanol.
Q = ne
- F = 7,2 102 x9,65 104=6,9 107 C.
Il est envisagé d’utiliser la quantité d’électricité de la pile à
combustible pour
recharger la batterie d’un bateau. Cette batterie, de tension nominale
12 V, est
capable de débiter un courant électrique d’intensité supposée constante
I = 4,2 A
pendant la durée d’utilisation.
B.4. Déterminer la valeur de la durée maximale pendant laquelle la
batterie du
bateau pourrait fonctionner après recharge. Expliquer en quoi la valeur
obtenue est
vraisemblablement surestimée.
Q = I t ; t = 6,9 107 /4,2 =1,7 107 s soit 4,6 103 heures.
Un partie de l'énergie fournie par la pile à combustible est dissipée par effet Joule ( énergie thermique).
|
|