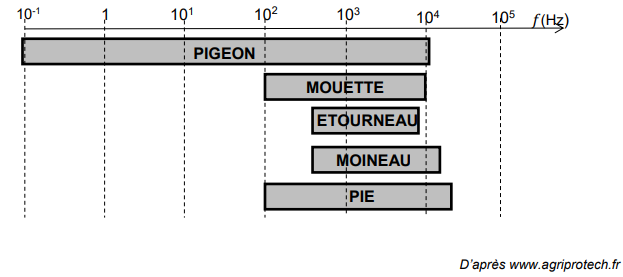
Effaroucheur d'oiseaux, bac STI2D Mayotte 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... L’effaroucheur d’oiseaux est un outil de prévention et de lutte contre le risque aviaire. Il émet des sons de fréquence comprise entre 300 Hz et 5 kHz. Les oiseaux ont une audition dont le spectre en fréquence couvre une bande de fréquences différente selon les espèces. Une solution pour les faire fuir consiste à émettre des cris d'oiseaux en détresse ou des cris de prédateurs. Les caractéristiques techniques du haut-parleur de l’effaroucheur sont données cidessous :  Dimensions : 230 x190 x 80 mm. Alimentation : 12 V continu. Protection : fusible 5 A. Consommation en veille : 120 mA. Consommation en fonctionnement : 4,5 A. Gamme de température : − 20 °C à + 60 °C. Puissance acoustique de sortie : 30 W. Bande passante : 300 Hz à 5 kHz. Niveau sonore mesuré à 1 m des haut-parleurs > 120 dB. Protection contre les courts-circuits et surchauffe. D’après BTS aéronautique.  1. Déterminer la valeur de la puissance électrique absorbée par le haut-parleur de l'effaroucheur en fonctionnement. P = U I = 12 x 4,5 =54 W.  2. Indiquer si les fréquences utilisées par le haut-parleur sont adaptées pour faire fuir les oiseaux. La bande passante s'étend de 300 Hz à 5 kHz.  Elle couvre le spectre de fréquences des oiseaux.  3. Indiquer si ces fréquences sont audibles par l’oreille humaine. Justifier. Les fréquences comprises entre 20 Hz et 20 kHz sont audibles par l'oreille humaine.  La valeur de référence pour la vitesse du son, dans les conditions de l’expérience, est 𝑣 = 340 m∙s-1. 4. Déterminer la valeur de la longueur d’onde du signal de fréquence 300 Hz. l = c / f = 340 / 300=1,13 m. 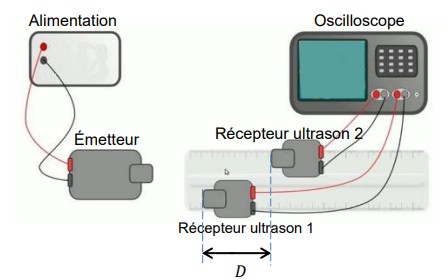Afin de vérifier la valeur de la vitesse de propagation de l’onde, un étudiant affirme : « comme la vitesse de propagation du son est identique à celle d’un ultrason, je vais utiliser un émetteur d’ultrasons afin qu’il émette des salves ; le récepteur 2 étant plus éloigné que le récepteur 1 de la source, je visualiserai un retard t sur l’oscilloscope me permettant d’en déduire la vitesse ». Les signaux enregistrés sont observés sur le chronogramme ci-dessous. La distance entre les deux récepteurs est 𝐷 = 18,1 cm. La base de temps de l’oscilloscope est réglée sur 100 µs/div. 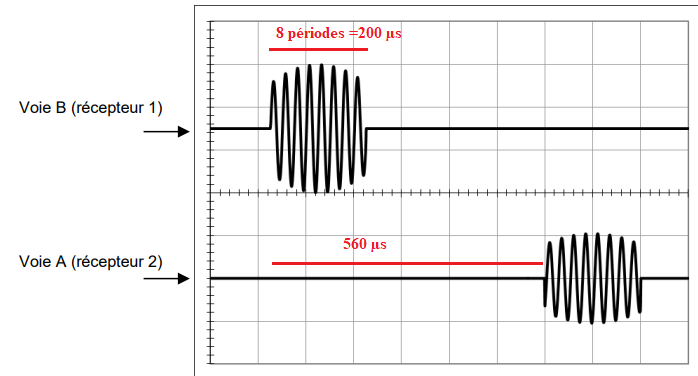5. Déterminer la valeur de la fréquence du signal émis. En déduire que l’étudiant a bien utilisé des ultrasons. 8 T = 200 ; T = 25 µs ; f = 1 /T = 1 /(25 10-6) =4,0 104 Hz = 40 kHz. Cette fréquence appartient au domaine des ultrasons.  Par une méthode statistique (type A), l’étudiant détermine que l’incertitude-type sur la valeur expérimentale de la vitesse est 𝑢(𝑣) = 0,3 .102 m∙s -1 . 6. Déterminer la valeur expérimentale de la vitesse de propagation du son et l’exprimer en tenant compte de l’incertitude-type. Retard : 560 µs ; distance D  = 0,181 m ; c = 0,181 / (560 10-6)=323 m /s. v = (323 ±30 ) m/s. ... .... La source sonore S de l’effaroucheur d’oiseaux est assimilable à un point. On suppose que le son se propage selon un cône et que la surface sur laquelle se répartit la puissance acoustique est assimilable à une surface plane en forme de disque suivant la représentation ci-dessous.  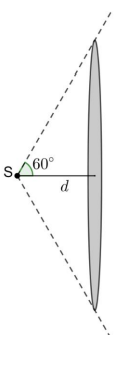7. Déterminer la valeur de la surface du disque situé à une distance 𝑑 = 1 m de la source S. tan 60 = Rayon du disque / d ; Rayon du disque= d tan 60 = 1 x tan 60 =1,73 m. Surface du disque : 3,14 x1,732 =9,4 m2.  8. En utilisant les caractéristiques techniques du haut-parleur de l’effaroucheur, vérifier que l’intensité acoustique I à 1 m de la source est proche de 3 W∙m-2 . Puissance acoustique de sortie : 30 W. I = P / S = 30 / 9,4 =3,2 W m-2.  On calcule le niveau sonore 𝐿 (en décibel dB) à partir de l’intensité acoustique 𝐼 par la relation : 𝐿 = 10 × log ( I / I0).  9. Conclure quant à la véracité de l’information fournie par le fabricant concernant le niveau sonore à 1 m des haut-parleurs. L = 10 log(3,2 / 10-12)=125 dB. Cette valeur est en accord avec celle annoncée 120 dB. ( écart relatif :(125-120) / 120 =0,04 ( 4 %).

menu