Mathématiques,
taxiage d'un avion bac STI2D Mayotte
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1.
L'objectif du dispositif étudié est de permettre le déplacement
autonome de l'avion au
sol, sans utiliser ses moteurs principaux (réacteurs) mais des moteurs
électriques.
Cette solution garantit une réduction des nuisances sonores et des
émissions de CO2.
L’utilisation des moteurs électriques diminue aussi fortement
l’ingestion de corps
étrangers (oiseaux) par les réacteurs sur le tarmac. La solution
étudiée consiste en une
motorisation électrique des deux trains principaux de l’avion (un
moteur électrique par
train). Lors des phases de déplacement au sol, l'avion est propulsé par
ses moteurs
électriques, au lieu de ses réacteurs. (aq).
Toute l’étude est réalisée lors d’un taxiage avant un décollage sur sol
horizontal en
charge maximale.
L'avion, initialement à l’arrêt, démarre sur un sol horizontal et
atteint une vitesse
maximale 𝑣max. On modélise la vitesse de l’avion, exprimée
en m∙s -1
, par une fonction f définie sur [0 ; +∞[ par f(t) = 𝐴 × (1 − 𝑒
−0,13𝑡
) où 𝐴 est une constante réelle et 𝑡
est le temps exprimé en seconde.
1. Exprimer en fonction
de 𝐴,la limite en plus l'infini de f(t).
Le terme en exponentielle tend vers zéro et f(t) tend vers A.
La représentation graphique de cette fonction est donnée sur le
graphique ci-après. Elle
modélise les valeurs expérimentales représentées par des croix sur ce
graphique.
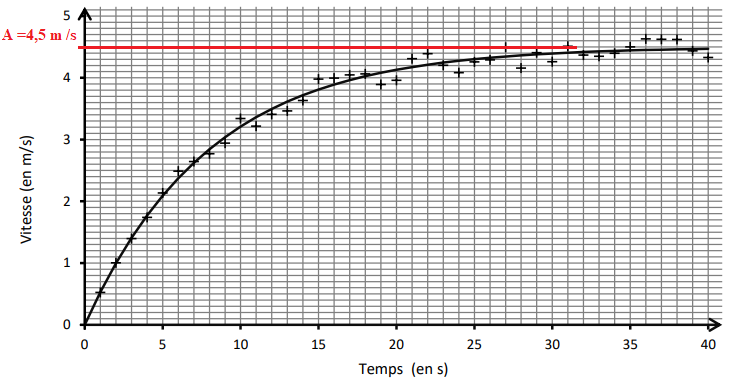
2. Conjecturer la valeur de 𝐴 à
l’aide du graphique.
La vitesse de l’avion, exprimée en m∙s
-1
, est modélisée par la fonction v définie sur
[0 ; +∞[ par v(𝑡) = 4,5 × (1 − 𝑒 −0,13𝑡
). On admet que v est dérivable sur [0 ; +∞[
et on note v′ la dérivée de v.
3. Montrer que v
′
(𝑡) = 0,585 × 𝑒
−0,13𝑡
. En déduire l’accélération initiale de l’avion.
v'(t) = 4,5 x0,13 e-0,13t = 0,585 × 𝑒
−0,13𝑡 .
L'accélération est la dérivée
de la vitesse par rapport au temps.
L'accélération initiale vaut
0,585 m s-2.
4. Préciser la direction et le sens
de la force de traction FT exercée par les moteurs
électriques sur l’avion.
Horizontale et dans le sens du déplacement.
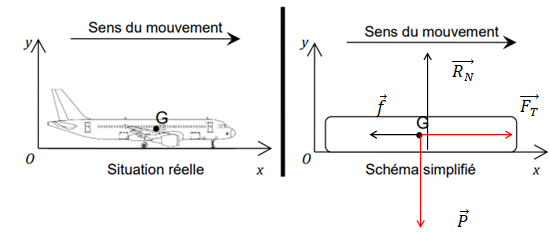
5. Recopier le schéma
simplifié sur votre copie et représenter en G, sans souci
d’échelle, toutes les forces s’exerçant sur l’avion. Indiquer le nom de
chacune de
ces forces.
Poids, action du plan, forces de frottement et force de traction.
6. On se place à
l’instant 𝑡 = 0 s. En appliquant le principe fondamental de la
dynamique, montrer que si l’on néglige les forces de frottement, on
peut écrire
𝐹𝑇 = 𝑚 × 𝑎.
Ecrire la seconde loi de Newton sur l'axe Ox.
FT = ma.
7. En déduire la valeur
de la force de traction exercée par chacun des moteurs
électriques lors du démarrage de l’avion, sachant que l’accélération à
𝑡 = 0 s
est estimée à 0,585 m∙s
-2
.
Masse au décollage m = 73 500 kg.
FT = 73500 x0,585 =4,3 104 N pour les deux
moteurs.
4,15 104 N pour un moteur.
|
...
|
....
|
Mathématiques.
Question 1.
𝑔 est une fonction définie et dérivable sur [0 ; +∞[.
On admet que la dérivée de 𝑔 est la fonction 𝑔′ définie sur [0 ; +∞[
par :
𝑔
′
(𝑡) = 6𝑒 −𝑡
(1 − 𝑡).
1. Étudier le signe
de 𝑔′(𝑡) sur [0 ; +∞[.
2. En déduire les
variations de 𝑔 sur [0 ; +∞[.
Le terme en exponentielle est positif ; g '(t) a le signe de 1-t.
si t appartient à [0 ; 1], g '(t) est positive et g (t) est croissante.
si t appartient à [1 ; +oo [, g '(t) est négative et g (t) est
décroissante.
g(t) présente un maximum pour t = 1.
Question 2.
Le plan est muni d’un repère orthonormé .
Soit A et B les points d’affixes respectives :
zA = exp(
𝑖
5p /
6) et zB = exp(
-𝑖 2p / 3).
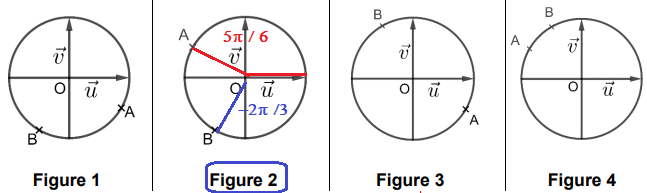
1. Les points A et B sont correctement représentés sur l’une des
figures ci-dessous.
Laquelle ? Aucune justification n’est attendue.
2. Montrer qu’un
argument de zA /
zB est −𝜋
/ 2
.
Argument de zA /
zB : 5p
/
6 -(-2p / 3) =5p /
6 +4p / 6 = 9p / 6 =3p / 2 ou −𝜋
/ 2
.
Question 3.
Résoudre dans ]1 ; +∞[ l’équation :
ln(𝑥 − 1) + ln(𝑥 + 1) + ln(𝑥) = ln(𝑥
2 − 1) − ln(0,5).
ln[ (x-1)(x+1)x] =ln((x2-1) /0,5) =ln(2(x2-1))
(x-1)(x+1) x =2(x2-1).
(x2-1) x = 2 (x2-1).
x = 2.
Question 4.
On considère l’équation différentielle (E) : 𝑦
′ = −𝑦 + 2.
1. Déterminer
l’ensemble des solutions de l’équation différentielle (E).
Solution générale de y'+y =0 : y = A e-x avec A une
constante.
Solution particulière de (E) : y=2.
Solution générale de (E) : y = A e-x +2.
2. En déduire la
solution 𝑓 de l’équation différentielle (E) qui s’annule en 0.
0 = A+2 soit A = -2.
y = -2 e-x +2.
Question 5.
Soit la fonction 𝑓 définie sur R par 𝑓(𝑥) = 𝑥
2 − 2𝑒
𝑥
.
1. Montrer que pour tout
réel 𝑥 de R , f(x) = 𝑒
𝑥
(𝑥
2𝑒
−𝑥 − 2).
𝑓(𝑥) = 𝑥
2 ex e-x− 2𝑒
𝑥 = 𝑒
𝑥
(𝑥
2𝑒
−𝑥 − 2).
2. En déduire la limite
en plus l'infini de
𝑓(𝑥).
En olus l'infini e-x tend vers zéro.
𝑥
2𝑒
−𝑥 tend vers zéro.
𝑥
2𝑒
−𝑥 − 2 tend vers -2.
𝑒
𝑥 tend vers plus l'infini.
f(x) tend vers moins l'infini.
Question 6. On
considère un signal électrique dont l’expression en fonction du temps
𝑡 est donnée
par :
𝑢(𝑡) = √3cos(𝑡) − sin(𝑡).
1. Montrer
que le signal 𝑢 peut s’écrire pour tout 𝑡 réel sous la forme :
𝑢(𝑡) = 2cos (𝑡 +
𝜋
/ 6
).
𝑢(𝑡) =2 [ √3 / 2 cos(𝑡) −1 /2 sin(𝑡)].
u(t) = 2 [ cos (-p/6)
cos(𝑡) +sin (-p/6)
sin(𝑡)].
u(t) =2cos (𝑡 +
𝜋 /
6
).
2. Résoudre dans [0 ;
𝜋[, l’équation 𝑢(𝑡) = 1.
2cos (𝑡 +
𝜋 /
6
) =1.
cos (𝑡 +
𝜋 /
6
) =0,5.
cos (𝑡 +
𝜋 /
6
) =cos (p/3)
t +p /6 = ±p /3 +2kp.
t = ±p /3 -p /6+2kp.
t = p /6+2kp.
t = -p /2+2kp.
|
|