Refroidissement
d'un lait, le son de la guitare, mathématiques, bac STI2D Métropole
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
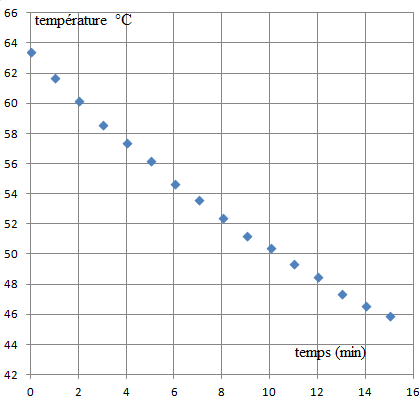
Afin d’étudier l’évolution de la
température d’une masse de liquide en contact avec
l’atmosphère d’une pièce en fonction du temps, l’expérience suivante
est réalisée.
Une masse de lait écrémé m = 150 g est chauffée à une température de
63,4 °C. On
laisse ensuite le lait se refroidir à l’air libre en relevant sa
température toutes les
minutes.
Pendant toute la durée de l’expérience, la température de l’air de la
pièce reste
constante et inférieure à celle du lait.
1. Citer les trois
modes de transferts thermiques.
Conduction, rayonnement et convection.
2. Préciser, en le
justifiant, le sens du transfert thermique entre la masse de lait et
l’air de la pièce.
Transfert du corps chaud, le lait, vers l'air de la pièce ( corps le
plus froid).
3. Calculer,
d’après les résultats expérimentaux, la valeur du transfert thermique Q
entre la masse de lait et l’air de la pièce entre les dates 𝑡 = 1 min
(61,7 °) et 𝑡 = 2 min (60,2°C).
Sans calcul, préciser si la valeur du transfert thermique est plus
petite ou plus
grande que 𝑄 entre les dates 𝑡 = 6 min et 𝑡 = 7 min.
Capacité thermique massique du lait C = 4,0 kJ kg-1 K-1.
Q = mC Dq =0,15 x
4,0 x(60,2-61,7)= -0,9 kJ.
Entre les dates t =6 min et t = 7 min, |Q| sera plus faible car
l'intervalle de température est plus petit.
La température du lait, exprimée en degré Celsius, en fonction du temps
t, exprimé
en minute, est modélisée par la fonction T définie sur [0; +∞[ par :
T(t)) = 37×exp(
− 20 t/
459) + 26,4.
4. Calculer T(0) et
interpréter ce résultat dans le contexte de l’exercice.
T(0) = 37 +26,4 =63,4 °C, température initiale du lait.
5. Déterminer la limite
de T en plus l'infini.
Selon ce modèle, quelle est la température de l’air de la pièce ?
Justifier.
Le terme en exponentielle
tend vers zéro et le lait a la température de la pièce soit 26,4°C.
6. Selon ce modèle,
au bout de combien de temps la température du lait vaut-elle
40°C ? Donner le résultat en minute et seconde.
40 =37×exp(
− 20 t/
459) + 26,4.
13,6 =37×exp(
− 20 t/
459).
13,6 / 37 =0,368 =exp(
− 20 t/
459).
ln(0,368) = -1,00=− 20 t/
459.
20t = 459 ; t = 459 /20 =22 min 57 s.
Le son
de la guitare.
1. Les
cordes de guitare
Les cordes de guitare sont un élément essentiel pour la
production du son. C'est la
vibration de celles-ci qui est transformée en signal électrique par les
micros de la
guitare. Ainsi les cordes sont le plus souvent en alliage de fer pour
pouvoir interagir
avec les aimants présents dans les micros.
A l'air libre les cordes s'oxydent progressivement car elles sont le
siège de réactions
d'oxydoréduction.
Dans l’air humide, du fait de la condensation, la transformation
chimique peut être
modélisée à l’aide des deux demi-équations électroniques suivantes :
Fe(s) +2HO-
(aq) = Fe(OH)2(s) + 2 e-.
O2(g) + 2 H2O(l) + 4 e- = 4 HO-
(aq)
1.1. À partir des
deux demi-équations proposées, écrire l'équation de la réaction
d'oxydoréduction qui modélise la transformation chimique subie par le
fer
contenu dans les cordes.
2Fe(s) +4HO-
(aq) = 2Fe(OH)2(s) + 4 e-.
O2(g) + 2 H2O(l) + 4
e- = 4 HO-
(aq)
Additionner et simplifier :
2Fe(s)
+4HO-
(aq) +O2(g) + 2
H2O(l) + 4 e-= 2Fe(OH)2(s) + 4 e-+ 4 HO-
(aq)
2Fe(s) +O2(g)
+ 2 H2O(l)=
2Fe(OH)2(s) .
1.2. Montrer qu’il est
justifié de considérer que le fer subit une oxydation dans cette
transformation chimique.
Le fer libère des électrons, c'est un réducteur qui s'oxyde.
Afin de limiter cette oxydation, une des méthodes actuelles consiste à
recouvrir la
corde avec un enduit transparent très fin qui sert de revêtement à la
corde.
1.3. Indiquer
la propriété que doit posséder l’enduit pour éviter efficacement le
phénomène d'oxydation.
L'enduit doit former une couche homogène imperméable au dioxygène de
l'air.
Conséquences de
l'oxydation des cordes sur le son d'une guitare.
En utilisant la même échelle verticale, on réalise le spectre
d'amplitude d'une note
jouée par une guitare électrique équipée de cordes neuves puis de
cordes oxydées.
1.4. À partir du spectre obtenu pour
la corde neuve, déterminer, en justifiant la
fréquence fondamentale de la note jouée.
1.5. Indiquer la note
jouée par la guitare.
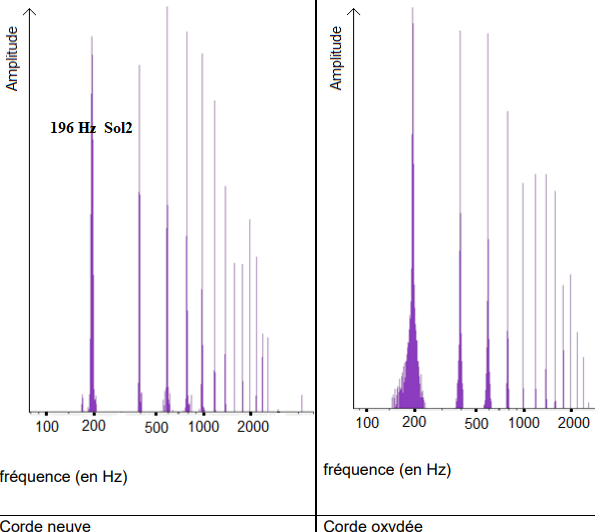
1.6. Indiquer, en
justifiant, si le son produit par la corde neuve a la même hauteur
que celui produit par la corde oxydée.
Oui, les fréquences du fondamental sont identiques.
1.7.
Préciser, en justifiant, quelle caractéristique du son produit par la
guitare est
modifiée selon que l’on utilise des cordes neuves ou oxydées.
Les harmoniques n'ont pas la même amplitude : le timbre est modifié.
2. Le câble reliant la
guitare à l'amplificateur.
Les musiciens évoquent souvent l’influence du câble reliant la
guitare à
l’amplificateur sur le son obtenu. Selon eux, le câble provoquerait une
diminution
d’amplitude des harmoniques de hautes fréquences, produisant un son
plus terne,
moins riche en composantes aigues.
Nous réalisons deux études afin de vérifier la pertinence de cette
observation.
Une première étude est réalisée sur un câble de guitare d'une longueur
de 10 m, non
relié à la guitare. Il s’agit de déterminer une éventuelle atténuation
du signal
électrique transporté par le câble.
Une tension sinusoïdale de fréquence connue est délivrée par un
générateur basses
fréquences. À l'aide d'un oscilloscope, l'amplitude Ue de la tension en
entrée du câble
est comparée à l'amplitude Us de la tension en sortie du câble.
On peut calculer alors l’affaiblissement R (en dB) subi par le signal
lors de de son
transport par le câble grâce à la relation suivante :
Ue /
Us
=10 R /
20
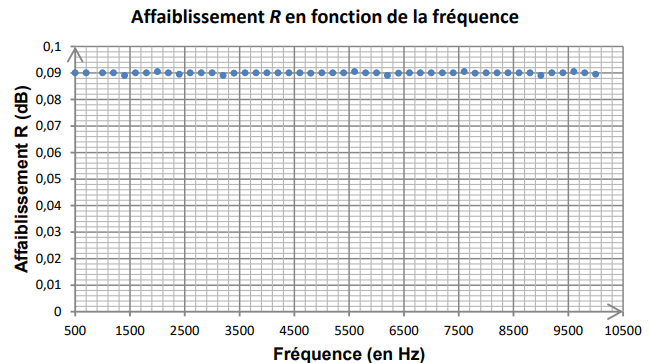
Les mesures de l’affaiblissement généré par le câble pour des signaux
sinusoïdaux
de fréquence comprise entre 500 Hz et 10 kHz permettent d’établir le
graphe suivant.
2.1. Montrer qu'une
valeur d’affaiblissement positif correspond à une atténuation
du signal lors du passage dans le câble.
Si R est positif, Us =
Ue x10 -R /
20 ; 10
-R /
20 < 1 et Us
<
Ue.
2.2. En considérant une tension
d'entrée d’amplitude Ue = 20,0 mV, déterminer la
tension de sortie dans les conditions de l'expérience, pour une valeur
de
l’affaiblissement R = 0,09. Commenter le résultat.
Us =
Ue x10 -R /
20 =20,0 x10-0,0045=19,8 mV.
L'affaiblissement est très faible ( 1 %).
2.3. Exploiter la courbe ci-dessus
pour déterminer si les propriétés électriques du
câble seul peuvent expliquer une modification du timbre du son obtenu.
Justifier la réponse.
Les propriétés électriques du
câble seul peuvent pas expliquer à elles seules une modification du
timbre du son obtenu, car l'affaiblissement est le même pour toutes les
fréquences.
Cette première
expérience ne prenant pas en compte le branchement de la guitare
sur le câble et sur l’amplificateur, on réalise une seconde étude en
connectant le
câble, en entrée et en sortie, à des dipôles ayant respectivement des
propriétés
électriques semblables à celles de la guitare et de l’entrée de
l’amplificateur.
Pour isoler l’influence du câble, on réalise des mesures
d’affaiblissement avec un
câble très court puis avec le câble de 10 m. On obtient les graphiques
ci-dessous.
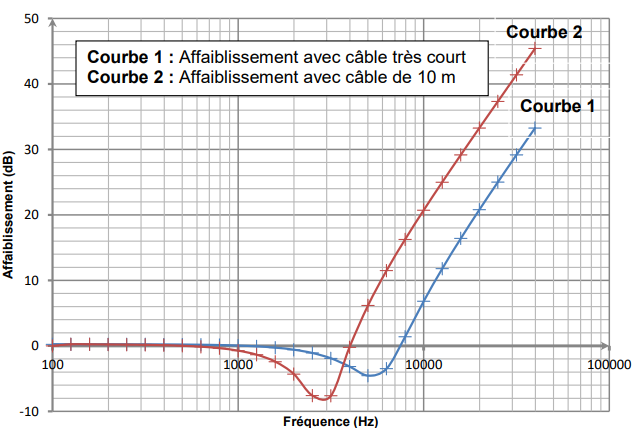 2.4. En ne considérant que les
fréquences pour lesquelles l’affaiblissement R a
une valeur positive, indiquer si l’allure de ces graphiques est
compatible avec
les problèmes évoqués par les musiciens lors de l’utilisation d'un long
câble.
2.4. En ne considérant que les
fréquences pour lesquelles l’affaiblissement R a
une valeur positive, indiquer si l’allure de ces graphiques est
compatible avec
les problèmes évoqués par les musiciens lors de l’utilisation d'un long
câble.
L'affaiblissement est d'autant plus grand que le câble est long et que
les fréquences sont plus élevées. En accord avec l'observation
des musiciens.
|
...
|
....
|
Mathématiques.
Question
1
1. Montrer, en détaillant vos calculs, que :
ln(2025) = 4 ln(3) + 2 ln(5).
2025 =25 x81 =52 x 34 ;
ln(2025) = ln (52) + ln(34) = 4 ln(3) + 2 ln(5).
2. Simplifier le
nombre 𝐴 ci-dessous en détaillant les calculs :
𝐴 = 2 ln(e
4
) − 3 ln (
1
/e
).
A = 2 x4 ln(e) +3 ln(e) =8+3=11.
Question 2
On désigne par i le nombre complexe de module 1 et d’argument ½p.
On considère le nombre complexe suivant :
𝑧 =
(−1 + i) /
(3i)
.
1. Mettre z
sous forme algébrique. Détailler les calculs.
z = (-1+i ) i / (3 i2) = -(-i+i2) /3 =1 /3 +i / 3.
2. Mettre 𝑧
sous forme exponentielle. Détailler les calculs.
Module de z : |z| = (1/32 +1/32)½ =2½
/ 3.
z / |z| =1/2½ +i / 2½ = cos (p/4) + i sin(p/4).
z = 2½ / 3 exp(i p/4).
Question 3
On considère l’équation différentielle (𝐸) ∶ 2 𝑦
′ + 𝑦 = 0, où 𝑦 est une fonction de la
variable 𝑥, définie et dérivable sur R et 𝑦′ la fonction dérivée de
𝑦.
1. Déterminer les
solutions sur R de l'équation différentielle (𝐸).
y' +0,5 y =0.
f(x) = B exp(-0,5x) avec B une constante.
2. Le plan est muni
d'un repère.
Déterminer la solution f de (𝐸), dont la courbe représentative C dans
ce repère
passe par le point A(ln(9) ; 1).
1=B exp(-0,5 ln(9)) =B exp( 0,5(ln(1/9)) = B exp(ln(1 /9½))
= B exp(ln(1/3)= B / 3. B = 3..
f(x) = 3 exp(-0,5x).
Question 4
On considère la fonction f définie sur R par f(x) = a+bex
, où a et b sont deux
nombres réels.
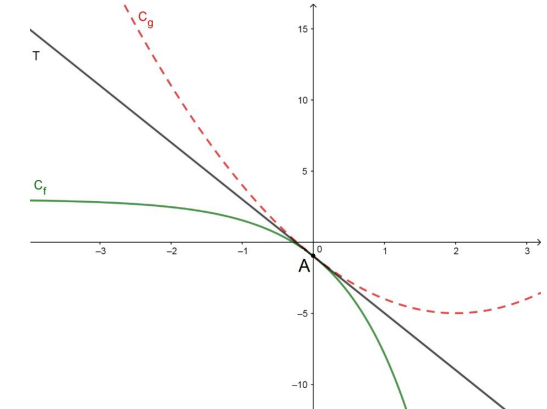
On considère la fonction g définie sur R par g(x) = x2-4x-
1.
On note 𝐶𝑓 et 𝐶𝑔 les courbes représentatives
des fonctions f et g, tracées dans le
repère orthogonal ci-dessous.
1.
On admet que les deux courbes 𝐶𝑓 et 𝐶𝑔 ont
un unique point en commun, noté A
d’abscisse 0.
Calculer 𝑔(0), puis en déduire que 𝑎 + 𝑏 = −1.
g(0) = -1. f(0) = a+b ; g(0) = f(0) ; a+b= -1.
2. On admet que les deux
courbes ont la même tangente 𝑇 au point A.
a. Donner,
pour tout réel x, une expression de g'(x) puis calculer g′(0).
g'(x) = 2x-4. g'0) = -4.
b. En déduire la
valeur de b, puis celle de a.
g'(0) = f '0) =be0 = b = -4.
par suite a = 3.
Question 5
Soit g la fonction définie sur l’intervalle ]0 ; +∞[ par :
𝑔(𝑥) = 0,5 x2 – ln(𝑥).
1. On admet que 𝑔
est dérivable sur l’intervalle ]0 ; +∞[ et on note 𝑔′ sa fonction
dérivée. Montrer que pour tout réel 𝑥 de l’intervalle ]0 ; +∞[,
𝑔
′
(𝑥) =
(𝑥−1)(𝑥+1) /
𝑥
.
g'(x) = x -1 /x = (x2-1) /x = (𝑥−1)(𝑥+1) /
𝑥
.
2. Montrer que la
fonction 𝑔 admet un minimum, dont on précisera la valeur exacte,
sur l’intervalle ]0 ; +∞[.
g'(x) a le signe de x-1.
Si x appartient à ]0 ; 1], g 'x) est négative et g(x) est décroissante.
Si x appartient à [1 ; +oo[, g 'x) est positive et g(x) est croissante.
Si x = 1, g'(x) est nulle et g admet un minimum.
g(1) =0,5 x12 -ln(1) = 0,5.
Question 6.
La tension 𝑢, exprimée en volt, aux bornes d’un dipôle en fonction du
temps 𝑡,
exprimé en seconde, est donnée par : 𝑢(𝑡) = cos(50𝑡) + √3sin(50𝑡).
1. Pour tout nombre
réel 𝑡, écrire 𝑢(𝑡) sous la forme 𝑢(𝑡) = 𝑈max cos(w𝑡 + f) où :
𝑈max représente la tension maximale (exprimée en
volt) ;
w
représente la pulsation (exprimée en rad.s-1
) ;
f représente
le déphasage (exprimé en rad).
𝑢(𝑡) =2(0,5 cos(50𝑡) + √3 / 2 sin(50𝑡)).
𝑢(𝑡) =2( cos (p /3)cos(50𝑡) + sin(p/3)sin(50𝑡)
u(t) = 2 sin(50 t + p /3)
2. En déduire la
fréquence correspondante 𝑓 = w
/ (2p)
, exprimée en Hz. Arrondir le
résultat à l’unité.
f = 50 /(2 x3,14) ~8 Hz.
|
|