Mathématiques, bac STI2D 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.
.. ..
......


...
Question 1.
On a tracé dans le repère orthonormé  la courbe représentative Cf de la fonction f définie sur ]0 ; + ∞[ par : f(x) = ln(x). On note A le point de Cf de coordonnées (e ; 1). On note T la tangente à la courbe Cf au point A. La tangente T passe-t-elle par l’origine du repère ? Justifier.

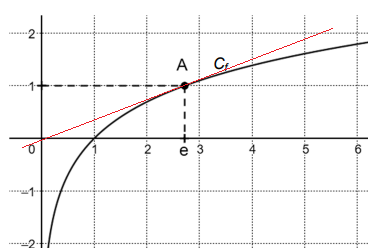
Coefficient directeur de la tangente : f '(e) = 1 /e.
Le point A appartient à la tangente : yA = 1 / e xA +b.
1 = e / e+b ; 1 = 1 +b ; b =0.
Equation de la tangente y = 1 /e x.
La tangente passe par l'origine.

Question 2.
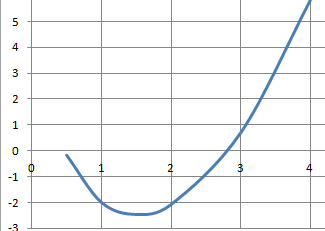
On considère la fonction f définie sur l’intervalle [0,5 ; 10] par : f(x) = x 2 – x – 2 – 3 ln(x). On note f ʹ la fonction dérivée de f.
 a. Montrer que f ʹ(x) = (x+1)(2x-3) / x pour tout x appartenant à l’intervalle [0,5 ; 10].
f '(x) = 2x-1-3 / x = (2x2-x-3) / x.
Or (x+1)(2x-3) = 2x2-3x+2x-3 = 2x2-x-3.
b. Montrer que f admet un  un minimum sur l’intervalle [0,5 ; 10] et préciser la valeur exacte de ce minimum.
La dérivée s'annule pour x = 1,5 et x=-1 ( cette valeur n'appartient pas à l'intervalle [0,5 ; 10].
Sur cet intervalle : x+1 >0 et x > 0.
2x-3 < 0 si x appartient à [0,5  ; 1,5[ ; f '(x) négative et f(x) est strictement décroissante.
2x-3 > 0 si x appartient à ]1,5  ; 10] ; f '(x) positive et f(x) est strictement croissante.
x = 1,5 , f '(x) = 0 et f(x) présente un minimum.
f(1,5) = 1,52 -1,5 -2-3ln(1,5) = -1,25 -3 ln(1,5).


Question 3.
 a. Résoudre dans R l’équation e – 0,0434 x = 0,01. On donnera la valeur exacte de la solution.
-0,0434 x = ln (0,01) ; x = - ln(0,01) / 0,0434.
 b. Un signal de puissance initiale P(0) = 6,75 mW parcourt une fibre optique. La puissance du signal, exprimée en mW, lorsque celui-ci a parcouru une distance de x kilomètres depuis l’entrée est donnée par P(x) = 6,75 e – 0,0434 x . Quelle est la distance parcourue par le signal lorsque celui-ci aura perdu 99 % de sa puissance ? On arrondira le résultat obtenu au kilomètre.
0,01 P(0) =0,00675 = 6,75 e – 0,0434 x .
e – 0,0434 x  =0,01 ; x = - ln(0,01) / 0,0434 ~ 106 km.

...
....

 Question 4.
Le plan complexe est muni d’un repère orthonormé direct. On considère les points A et B d’affixes respectives :
 zA = 3 exp(-ip /3) et zB = – 1 + i 3½ . Les points O, A et B sont-ils alignés ?
|zB| =[(-1)2 +3]½ =2.
zB / |zB| = -0,5 +i 3½ /2 =cos ( 2p/3) + i sin( 2p/3).
zB = 2 exp( i 2p/3).
zB / zA = 2 / 3 exp ( i (2p/3 +p/3)) = 2 /3 exp(ip)= -2 /3.
zB = -2 /3 zA.
Les points O, A et B sont alignés.



Question 5.
On considère la fonction f définie sur l’intervalle [1 ; 2] par : f(x) = x + e x –1 / x .
 On a tracé dans le repère orthonormé  la courbe représentative C de la fonction f.
On considère les points A(1 ; 0) ; B(2 ; 0) ; C(1 ; 2) ; D(2 ; 8) ; E(1 ; 3) et F(2 ; 9).
On admet que la courbe C est au-dessus du segment [CD] et en dessous du segment [EF].
 a. À l’aide du graphique, donner un encadrement d’amplitude 1 de l’intégrale :.
 b. Calculer la valeur exacte de
Aire du triangle CHD :1 x 6 / 2 = 3
Aire du rectangle ABCH : 1 x2 = 2.
Total : 5.

Aire du triangle EKF :1 x 6 / 2 = 3
Aire du rectangle ABEk : 1 x 3 = 3.
Total : 6.

Primitive de f(x) : 0,5 x2 +ex -ln(x).
Intégrale : F(2)-F(1).
F(2) = 2 +e2 -ln(2)
F(1) =0,5+e.
F(2)-F(1) =1,5+e2-e-ln(2) ~5,48.


.
Question 6.
La tension u aux bornes d’un générateur, exprimée en volt, dépendant du temps t, exprimé en seconde, est donnée à l’instant t par :
 u(t) = 120 cos(70t) – 120 sin(70t).
 a. Montrer que, pour tout t de l’intervalle [0 ; + ∞[, u(t) = 120x2½ cos (70t +p/4) .
cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
a = 70 t ; b = p/4.
cos (70t +p/4)  =cos (70 t) x cos (p/4) -sin(70t) sin(p/4)=2½ / 2 [cos (70 t) -sin(70t)].
120x2½cos (70t +p/4) = 120 [cos (70 t) -sin(70t)].

 b. En déduire la fréquence f = w / (2p) , exprimée en Hz, délivrée par le générateur, où w désigne la pulsation. On arrondira le résultat à l’unité.
w = 70 rad /s ; f = 70 / 6,28 ~11 Hz.

  
menu