Recuit de détente.
Pour réaliser un recuit de détente, on dispose d’un four thermique
électrique qui
permet d’obtenir progressivement la température souhaitée à l’aide
d’une résistance
chauffante.
Le four étudié ici a une puissance de 2,0 kW.
La température au sein du four contenant les pièces en acier, dépendant
du temps,
est modélisée par une fonction
q.
La température est exprimée en degré
Celsius et
le temps est exprimé en seconde.
On admet que la fonction
q,
définie et dérivable sur l’intervalle [0 ;
+∞[, est une
solution, sur cet intervalle, de l’équation différentielle suivante :
(E) : 800 y ′ + y = 600.
À l’instant t = 0, on met le four sous tension. La température
est
alors de 25 °C.
1. À partir de
l’équation différentielle ci-dessus, déterminer une
durée
caractéristique de l’évolution de la température dans le four et la
valeur limite
atteinte par la température du four.
y ′
+ y / 800= 0,75.
Durée caractéristique : 800 s.
Valeur limite de la température du four : 600 °C.
2. a.
Montrer que la fonction
q
est définie sur [0 ; +∞[ par :
q(t)
= 600 – 575 e
– 0,00125 t
.
q' =
-575 x(-0,00125)
e –
0,00125 t
=0,71875e – 0,00125 t ;
repport dans (E) : 800 x0,71875e –
0,00125 t + 600 – 575 e –
0,00125 t
=600, c'est bien vérifié quelque soit le temps..
b. Quelle sera la
température du four au bout de 10 minutes ?
10 min = 600 s.
q(t=600) = 600 – 575 e –
0,00125 x600 ~328 °C.
3. Selon la
norme NF EN ISO 4885, le recuit de détente doit se faire lorsque la
température du four est comprise entre 550 °C et 650 °C.
a. Selon ce
modèle, déterminer le temps d’attente nécessaire pour que le four
atteigne la température de 550 °C. On arrondira le résultat à la
minute.
550
= 600 – 575 e –
0,00125 t
.
50 =575 e – 0,00125 t
.
e – 0,00125 t
=50 / 575 =0,08695.
– 0,00125 t
= ln(0,08695)= -2,44.
t =2,44 / 0,00125 ~1674 s ou 33 minutes.
b.
Selon ce modèle, la température du four peut-elle
dépasser 600 °C ?
q
=600 – 575 e – 0,00125 t.
Non, au bout d'un temps très long, le terme en exponentielle est nul et
la température atteint sa valeur maximale 600 °C.
4. La capacité thermique
massique de l’acier étant c
m = 460 J.kg
-1.K
-1,
déterminer la
valeur de l’énergie E
charge nécessaire pour porter une
charge de 2,50 kg de la
température ambiante de 25 °C à la température de 550 °C.
En déduire alors la puissance moyenne dédiée à ce chauffage et
commenter le
résultat.
E
charge = m c
m (
qfin -
qdébut) =2,50
x460 x(550-25)~6,04 10
5 J.
Puissance moyenne = énergie / durée =
6,04 105 / 1674 ~360 W, valeur assez faible.
Piscine avec volet roulant.
Le but de l’exercice est d’étudier la possibilité de l’installation
d’une alimentation
autonome pour un volet roulant permettant de protéger et sécuriser la
piscine.
Le bassin de la piscine étudiée a les dimensions suivantes :
longueur : 7,0 m, largeur : 3,5 m et profondeur (fond plat) : 1,5 m.
Moteur : 3 tours / min ; tension d'alimentation 24 V ; intensité : 5,0
A ; puissance électrique : 120 W.
1.1. En vous aidant
de la fiche technique du moteur, et sachant que le rayon moyen de
l’ensemble arbre du moteur et volet est de l’ordre de 25 cm, évaluer la
vitesse
moyenne de déroulement du volet sur le bassin.
3 tours / min soit 3 x3,14 x2 x0,25 ~4,7 m / min.
1.2. Évaluer la
durée nécessaire pour couvrir toute la surface du bassin. Commenter.
longueur / vitesse = 7,0 / 4,7 ~1,5 min. C'est assez rapide.
1.3. Le rendement du
moteur étant de l’ordre de 90 %, déterminer la puissance
mécanique développée par le moteur. Quelle est la nature de la
puissance
dissipée ?
Puissance électrique x rendement = 120 x0,9 =108 W.
La puiissance dissipée est sous forme thermique.
1.4. Sachant que la
puissance mécanique développée par le moteur est égale au
produit du couple moteur par la vitesse angulaire, évaluer la valeur du
couple
moteur.
Vitesse angulaire : 3 / 60 x2 x3,14 =0,314 rad / s.
Couple moteur : 108 / 0,314 ~344 N m.
2. Étude de la
batterie.
Pour l’alimentation électrique du moteur, on utilise 2 batteries
12 V branchées en
série dont les caractéristiques sont les suivantes :
- tension d’utilisation : 12 V ;
- capacité : 8,0 A.h.
2.1. Exprimer puis
calculer la valeur de l’énergie en W.h contenue dans chacune des
batteries.
12 x 8 = 96 Wh.
2.2. La durée
d’un cycle du volet roulant (ouverture et fermeture) étant de l’ordre
de 3
minutes, déterminer l’énergie électrique nécessaire à un cycle
d’utilisation du volet
roulant.
On rappelle que la puissance électrique consommée par le moteur est de
120 W.
Energie ( J) = puissance (W) x durée (s) =120 x 3 x 60 =2,16 10
4
J ou 2,16 10
4 / 3600 = 6 Wh.
2.3. Au bout
de combien de cycles faut-il recharger les batteries ?
96 x2 / 6 =32 h.
3. Étude du panneau
photovoltaïque.
La notice technique du panneau photovoltaïque permettant la recharge de
la batterie
précédente nous indique les caractéristiques suivantes (dans les
conditions standard
de test : ensoleillement de 1000 W/m
2 et 25 °C :
- puissance crête : P
c = 100 W ;
- courant de court-circuit : I
cc = 2,91 A ;
- tension à vide : U
co = 44,10 V ;
- tension à puissance crête : U
max = 36,50 V ;
- courant à puissance crête : I
max = 2,74 A.
3.1.
Compléter la caractéristique I = f(U) donnée en y indiquant le point de
fonctionnement à la puissance crête.
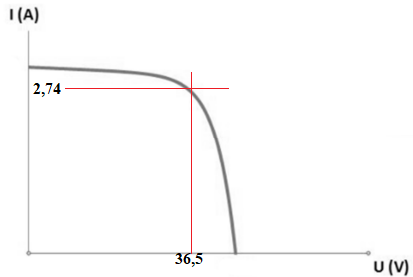 3.2.
3.2. Parmi les
trois montages électriques donnés, indiquer celui permettant de mesurer
la tension à vide et celui permettant
de mesurer une intensité de court-circuit.
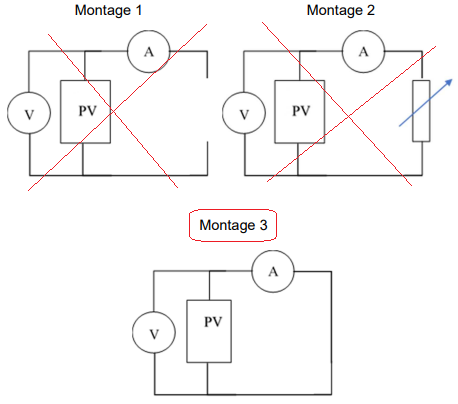 3.3.
3.3. Déterminer la durée
de recharge complète des batteries précédemment étudiées
lorsque le panneau fonctionne en délivrant sa puissance crête.
Puissance crète (W) x durée (h) =énergie ( Wh).
100 x durée =96 x2.
durée = 1,92 ~ 2 heures.