Thermique, son, pile au méthanol, Solar Impulse, bac STI2D 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.


.
.
.. ..
......


...

Evolution de la température d'une boisson. 4 points.
Une boisson chaude est servie dans une tasse en céramique.
1. Identifier un mode de transfert thermique mis en jeu entre la boisson chaude et la tasse, ainsi qu'entre la boisson et l'air ambiant.
Transfert par conduction entre la tasse et la boisson.
Transfert par convection entre la boisson et l'air.
On donne l'évolution de la valeur de la température de la boisson au cours du temps ( seconde).
qn+1 = -0,002(qn-20) +qn avec q0 = 90°C.
2. Calculer q2 et q3.
q1 = -0,002(q0-20) +90= -0,002 x70 +90= 89,860°C. (89,9)
q2 = -0,002(q1-20) +90= -0,002 x69,86 +89,86= 89,72028 °C. (89,7)
q3 = -0,002(q2-20) +90= -0,002 x89,72028 +89,72028= 89,5408°C. (89,5).

Flux thermique F entre la tasse et l'air ambiant : F = m Cth Dq / Dt.
Masse de boisson m = 0,400 kg  de capacité thermique Cth = 4180 J kg-1 °C-1.
3. Calculer ce flux au cours de la première seconde.
F = 0,400 x 4180 (90-89,86) / 1 ~234 J.
4. Justifier le sens du transfert thermique.
Le flux thermique s'effectue de la boisson chaude vers l'air ambiant.

La consommation d'une boisson chaude à une température supérieure à 50°C engendre un risque de brûlures.
5. Completer le script python suivant  renvoyant la durée d'attente ( seconde) sans risque de brûlure.
deftemps()
n=0
theta = 90
while theta > 50
n=n+1
theta = -0,002*(theta-20) +theta
return n
La valeur renvoyée est 424.
6. Indiquer si après une attente de 10 minutes, cette boisson chaude peut être consommée sans risque de brûlure.
10 minutes = 600 secondes.
600 > 424, la température de la boisson sera inférieure à 50°C. Aucun risque de brûlures.

  Étude du son d'un violon  (6 points)
L'élève enregistre le son d'un violon à l'aide d'un microphone et d'un logiciel d'acquisition.

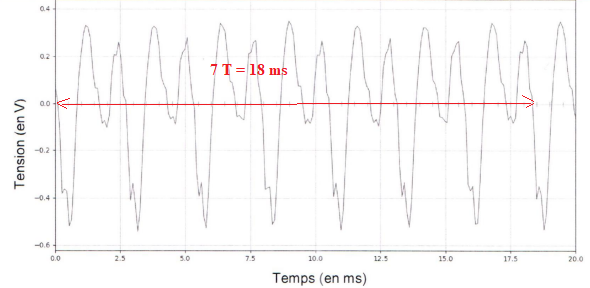
1. Déterminer la période T du son.
T = 18 / 7 =2,57 ms.
2. Vérifier que la fréquence est voisine de 390 Hz.
f = 1 / T = 1 /(2,57 10-3) ~390 Hz.
On donne le spectre d'amplitude du son du violon.

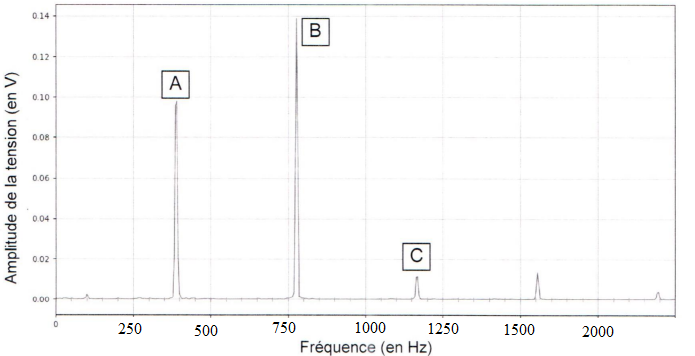
 3. Justifier que le pic A corresponde au fondamental.
Fréquence du pic A :~390 Hz.
4. 5 Donner les fréquences des harmoniques B et C.
B : f = 2 x390 = 780 Hz.
C : 3 x390 =1170 Hz.
Fréquence de l'harmonique de rang n : fn = 390 x n.
 . 6. Indiquer les rangs des harmoniques B et C.
B : harmonique de rang 2 ; C : harmonique de rang 3.

Pour générer un son complexe, l'élève utilise un microcontrôleur. Le son est enregistré de la même manière que celui du violon.
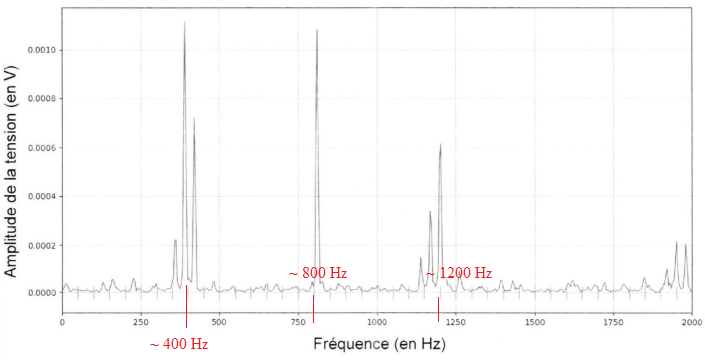7. Vérifier que le son produit par le microcontrôleur a la même hauteur que la note jouée par le violon.
Ces deux sons possèdent la même harmonique de rang 1 ( hauteur du son) soit environ 400 Hz.
8. Justifier que ces deux sons sont similaires.
Les harmniques de rang 1 et 2 sont à peu près identiques.
Les harmoniques de rang 3 diffèrent par leurs amplitudes.
   

...
....

 Pile à combustible au méthanol.
1. Nommer le type d'électrode où a lieu l'oxydation et celui où a lieu la réduction.
  2. Indiquer le sens du courant traversant la charge à l'extérieur de la pile et les polarités de la pile.

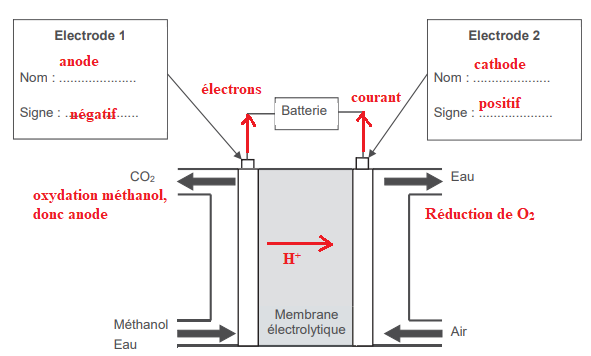
3. Etablir que l'équation du fonctionnement de la pile est :
2 CH3−OH(l) + 3 O2(g) --> 2 CO2(g) + 4 H2O(l)
Oxydation à l'anode :2 fois [CH3−OH(l) + H2O(l) --> CO2(g) + 6 H+ (aq) + 6 e- ]
Réduction à la cathode :3 fois [O2(g) + 4H+aq +4e---> 2H2O(l)].
Additionner et simplifier.
  4. Vérifier que la masse molaire du méthanol CH3OH est M = 32 g / mol.
M = 12 +4 +16 = 32 g / mol.
  5. Calculer la quantité de matière dans un litre de méthanol.
Masse volumique 0,792 g / L.
Masse de 1 L = 792 g.
n = 792 / 32 =24,75 ~24 mol.
6. Calculer la quantité de matière d'électrons.
CH3−OH(l) + H2O(l) --> CO2(g) + 6 H+ (aq) + 6 e-
n(e-) = 6 n = 6 x24,75 = 148,5 ~149 mol.
7. Déterminer la capacité Q de la pile en coulomb puis en Ah.
Q = n(e-) F = 148,5 x 96500 ~1,43 107 C ou 1,47 107 / 3600 =3,98 103 Ah.
8. Montrer que l'énergie utile délivrée par la pile est 12 kWh.
U = 12 V ; rendement 25 %.
énergie = QU x rendement= 3,98 103 x12 x 0,25 =1,194 104 Wh ~ 12 kWh.

Solar Impulse 2.
  L'avion Solar Impulse II a atteri à Abou Dhabi après avoir parcouru 43 041 km, avec comme seule source d'énergie, l'énergie solaire.
L'objectif de cet exercice est d'évaluer la masse de dioxyde de carbone qu'aurait rejeté un avion de mêmes caractéristiques réalisant un vol identique mais consommant du kérosène.
Kérosène (C10H22 ; liquide ; M = 142 g / mol )
 1. Donner la signification des pictogrammes ainsi que les précautions à prendre en manipulant du kérosène.

Travail loin de toutes flammes et sources de chaleur.
Port de masque, ne rien jeter à l'évier.
 2. Compléter l'équation de combustion du kérosène.
2 C10H22 (l) + 31O2(g) --> 20 CO2(g) + 22H2O(g).
On estime à 500 kg la masse de kérosène nécessaire à ce vol de 24 h.
3. Calculer la quantité de matière de kérosène.
n = m / M = 500 103 / 142 =3,52 103 mol.
  4. Montrer que la quantité de matière de dioxyde de carbone pour ce vol est 3,52 104 mol.
3,52 103 x 10 = 3,52 104 mol.
5. Calculer la masse de CO2 pour ce vol de 24 h.
3,52 104 M(CO2) =3,52 104 x 44 =1,55 106 g = 1,55 103 kg.
La durée du vol de Solar Impulse 2 a été de 560 h.
6. En déduire la masse de CO2 rejetée par un avion de mêmes caractéristiques réalisant le même vol, mais consommant du kérosène.
1,55 103 x550 / 24 =3,55 104 kg.

  
menu