Mathématiques,
physique chimie, bac STI2D Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Exercice 1. 4 points
Dans cet exercice, on étudie la chute d’un parachutiste, avant l’ouverture de son parachute, sous l’effet de son poids P.
On note f la force de frottement exercée par l’air et qui s’oppose à la
chute du parachutiste. Cette force est colinéaire et de sens opposé au
poids du parachutiste lors de sa chute.
Les schémas n° 1 et n° 2 représentent le parachutiste dans deux
situations différentes du saut avant qu’il n’ouvre son parachute.
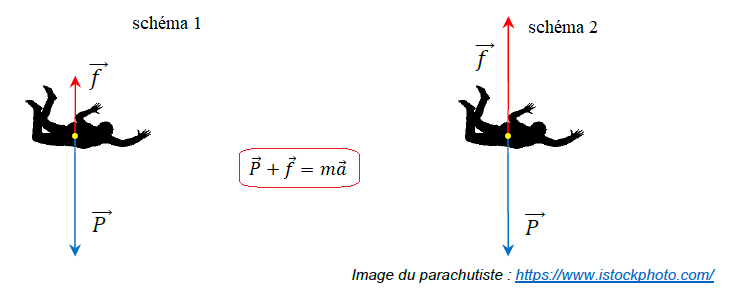
1.
Établir, à l’aide du principe fondamental de la dynamique, une relation
entre la masse m, l’accélération m, le poids m et la force de
frottement f.
Suivant un axe vertical orienté vers le bas : mg-f = ma.
a = g / f / m.
2. Indiquer, en
justifiant la réponse, si la vitesse du parachutiste augmente, est
constante ou diminue, pour chacune des situations 1 et 2.
Situation 1 : le poids l'emporte sur la force de frottement et la vitesse augmente.
Situation 2
: le poids et la force de frottement se neutralisent, le
mouvement est rectiligne uniforme ( norme de la vitesse constante).
Dans la suite de l’exercice, on modélise la vitesse du parachutiste (en m⋅s-1), en fonction du temps t écoulé (en seconde) depuis le largage, par la fonction v, solution de l’équation différentielle :
dv(t) / dt = -0,16 v(t) +9,81. (E)
On suppose que v(0)=0.
3. Démontrer que v(t)=981 / 16(1−e−0,16𝑡 ), pour t réel positif.
Solution générale de dv /dt +0,16 v=0 : v(t) =A exp(-0,16t) avec A une constante.
Solution particulière de (E) : v = 9,81 / 0,16 = 981 / 16.
Solution générale de (E) : v(t) =A exp(-0,16t) +981 / 16.
A t = 0, v(0) = 0 soit 0 = A+981 / 16 ; A = -981 / 16.
v(t) = -981 / 16 exp(-0,16t) +981 / 16.
v(t) = 981 / 16 (1-exp(-0,16 t)).
La brochure commerciale présentant le saut en parachute indique que le parachutiste atteint la vitesse de 200 km∙h-1 en moins de quarante secondes.
4. Convertir 200 km∙h-1 en mètre par seconde (m∙s-1).
200 / 3,6 ~56 m /s.
5. Valider ou infirmer l’indication de la brochure. Chute libre de 40 secondes. On descend à 200 km/h !
v(40) = 981 / 16(1-exp(-0,16 x40)) ~61 m /s.
Selon ce modèle, la vitesse atteinte à t = 40 s est proche de 220 km /h. L'affirmation est donc valide.
Exercice 2. 6 points.
Détermination expérimentale du rendement énergétique de l’électrolyse de l’eau
En prévision de la demande croissante en dihydrogène comme carburant
pour les voitures électriques équipées d’une pile à hydrogène, on
s’intéresse dans cet exercice à la production de dihydrogène par
électrolyse de l’eau et à son rendement.
Un électrolyseur est alimenté en électricité pour produire du dihydrogène à partir de l’eau.
1. Indiquer, sur le schéma le sens conventionnel du courant et le sens de circulation des électrons.
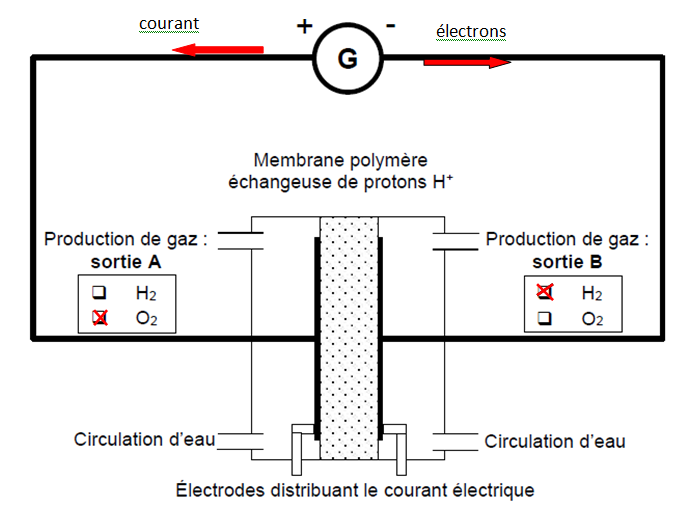
2. Indiquer la
demi-équation de la réaction qui se produit à l’électrode reliée à la
borne négative du générateur. Justifier la réponse.
Réduction de H+ à la cathode négative : 2 H+aq + 2e- --> H2 (g)
3. Indiquer la nature du gaz émis à chaque électrode en cochant les
cases correspondantes du schéma.
4. Montrer, à l’aide des deux demi-équations, que l’équation de la réaction d’électrolyse s’écrit :
2 H2O(ℓ) -->2 H2(g)+ O2(g).
Oxydation de l'eau à l'anode :
2 H2O(ℓ) -->O2(g)+4e- +4H+aq.
Réduction de H+ à la cathode négative : 4 H+aq + 4e- --> 2H2 (g).
Ajouter :
2 H2O(ℓ) + 4 H+aq + 4e- -->O2(g)+4e- +4H+aq + 2H2 (g)..
Simplifier :
2 H2O(ℓ) -->2 H2(g)+ O2(g).
Pendant le fonctionnement de l’électrolyseur, on mesure le volume V (en
millilitre) de dihydrogène produit en fonction du temps t (en seconde).
Les données obtenues sont rassemblées dans le tableau ci-dessous.
t(s)
|
0
|
18,4
|
34,5
|
53,2
|
73
|
88
|
107
|
125
|
141
|
V(mL)
|
0
|
2
|
4
|
6
|
8
|
10
|
12
|
14
|
16
|
On place les points associés aux données obtenues sur le graphique ci-dessous.
On ajuste le nuage de points par une droite, représentée en pointillés sur le graphique.
5. Proposer une démarche permettant de déterminer la valeur de la pente de la droite. Donner cette valeur et préciser son unité.
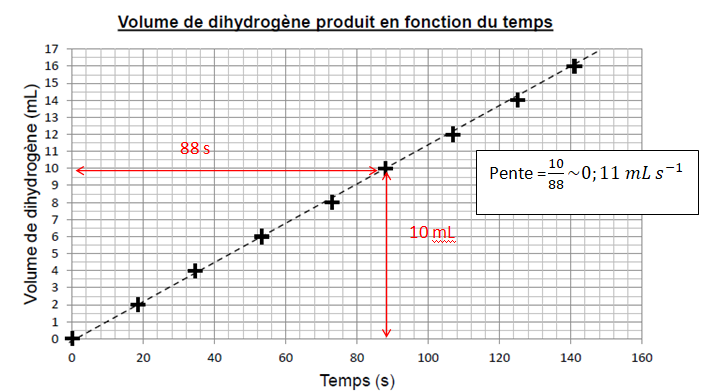
La valeur Pe de la puissance fournie par l’électrolyseur est
égale à 1,44 W. Lors du fonctionnement de l’électrolyseur, la valeur de
la tension aux bornes de l’électrolyseur, notée U, vaut 1,85 V et celle
de l’intensité du courant, notée I, vaut 1,14 A.
6. Indiquer sur le
schéma où placer un ampèremètre pour mesurer l’intensité du
courant I et un voltmètre pour mesurer la tension U.
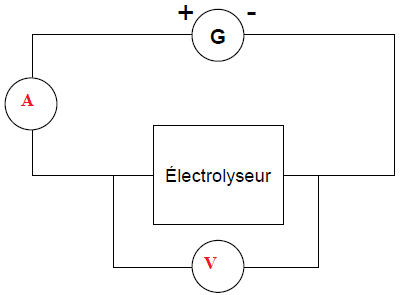
7. Calculer la puissance Pg fournie à l’électrolyseur.
Pg = U I =1,85 x 1,14 =2,109 ~2,1 W.
Le rendement d’un électrolyseur est défini par la relation h = Pe / Pg.
8. Calculer, en pourcentage, le rendement de l’électrolyseur.
1,44 / 2,109 ~0,68 ( 68 %).
Les électrolyseurs industriels ont un rendement compris entre 60 % et 75 %.
9. Comparer le rendement de l’électrolyseur étudié dans cet exercice au rendement des électrolyseurs industriels.
Cet électrolyseur a un rendement comparable au rendement des électrolyseurs industriels.
|
...
|
....
|
Exercice 3 (4 points)
Loi de refroidissement de Newton
Dans cet exercice, seulement 4 questions au choix parmi les 6 questions proposées sont à traiter.
Toutes ces questions sont indépendantes les unes des autres.
Pour chaque question, une
seule des quatre affirmations proposées est correcte. Pour les quatre
questions traitées, indiquer sur la copie l’affirmation choisie. Aucune
justification n’est demandée. Chaque réponse correcte rapporte un
point. Une réponse incorrecte, une réponse multiple, une absence de
réponse, ne rapportent ni n’enlèvent de point.
La loi de refroidissement de Newton indique que la vitesse de
refroidissement d’un matériau est proportionnelle à la différence entre
la température q (en degré Celsius) de ce matériau à l’instant t (en minute) et la température A constante de l’air ambiant.
Cela se traduit par la relation q '(t) =a (q(t)-A), où q
est la fonction définie et dérivable sur l’intervalle [0:+∞[ modélisant
la température du matériau en fonction du temps t, en prenant comme
origine du temps l’instant où la pièce en acier est mise à refroidir.
La valeur du coefficient a, qui est négatif, dépend du matériau.
Une pièce en acier, initialement à la température de 600 °C, est mise à
refroidir à l’air libre dans une pièce à 20 °C. Pour cet acier, a vaut −0,1.
1. La fonction q est solution de l’équation différentielle :
a. y=−0,1y ′+2
b. y=−0,1y ′+20
c. y ′=−0,1y+2 vrai
d. y ′=−0,1y+20.
q '(t) = -0,1 (q(t)-20) ; q '(t) = -0,1 q(t) +2.
Pour l’ensemble des questions suivantes, on admet que, sur l’intervalle [0 ; +∞[ , la fonction q est définie par :
q(t)=580 e−0,1t +20.
2. La pente de la tangente à la courbe représentative de la fonction q au point d’abs-cisse 10 vaut :
a. −58 / e vrai.
b. 580e−1+20
c. −58/ e+20
d. 580 /e.
q '(t) = -58e-0,1t ; q'(10) = -58 e-1 = -58 / e.
3. Sur l’intervalle [0 ; +∞[, la fonction q est :
a. croissante
b. décroissante vrai
c. croissante puis décroissante
d. constante.
q '(t) = -58e-0,1t ; e-0,1t >0 ; q '(t) < 0 et q(t) est strictement décroissante.
4. La limite en +∞ de q(t) est :
a. 20 vrai
b. 580
c. −∞
d. +∞.
q(t)=580 e−0,1t +20 ; en plus l'infini, e−0,1t tend vers zéro et q(t) tend vers 20.
La
pièce peut être manipulée lorsque sa température devient inférieure à
40 °C. Pour déterminer la durée minimale d’attente (en minutes), à
compter de l’instant où elle est mise à refroidir, on veut mettre en
place un algorithme de balayage, écrit en langage Python.

5. Pour que la
valeur renvoyée par la fonction duree_d_attente soit la valeur en-tière
minimale de la durée d’attente, la ligne 6 contient :
a. while t > 40 :
b. while Temperature > 40 : vrai
c. while Temperature < 40 :
d. for i in range(Temperature).
6. L’inéquation q(t) ≤ 40, d’inconnue t, admet comme ensemble solution sur [0 ; +∞[ :
a. l’intervalle [0 ;10 ln(1/29)]
b. l’intervalle [−10 ln(1/29) ;+∞[ vrai
c. l’intervalle [0 ; 10 / 29]
d. l’ensemble vide (pas de solution).
580 e−0,1t +20 < 40 ; 580 e−0,1t < 20 ; e−0,1t < 20 / 580 ; e−0,1t < 1 / 29 ; -0,1 t < ln(1 / 29) ; - 0,1 t < -ln( 29)
t > 10 ln( 29).
Exercice 4 au choix du candidat (6 points)
Vous indiquerez sur votre copie l’exercice 4 choisi : exercice 4 – A ou exercice 4 – B.
Exercice 4 – A
Mots clefs des principaux domaines abordés : ondes électromagnétiques ; transmission d’un signal.
Carte RFID
Une carte de cantine RFID (Radio Frequency IDentification) comporte une
puce électronique et une antenne formée d’un fil de longueur L enroulé
sur lui-même. La technologie RFID permet au lecteur de carte
d’identifier la personne qui passe et d’effectuer le décompte de ses
repas sur le réseau informatique du lycée. Lorsque l’on approche la
carte du lecteur de puce, celui-ci émet une onde électromagnétique.
Cette onde fournit, par induction, de l’énergie à la puce électronique
qui s’active et transmet alors un numéro d’identification au lecteur de
carte.
1. Déterminer, à
l’aide des documents 1 et 2 en fin d’exercice , à quel domaine des
ondes radio appartient chacune des trois fréquences utilisées en
communication RFID.
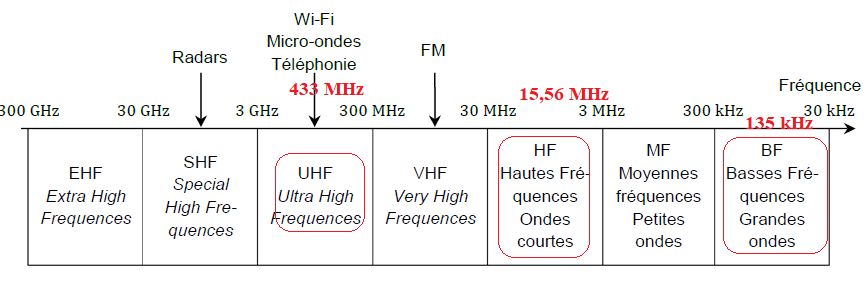
2. Citer deux arguments justifiant l’utilisation de plusieurs fréquences pour la communication RFID.
La fréquence est la caractéristique permettant d'établir la
communication entre la puce et l'antenne. Les puces n'ont pas la même
fonctionnalité. Plus la fréquence est élevée, plus la distance de
lecture s'agrandit.
A basse fréquence, la capacité de transmission des données est plus
faible, mais la capacité de lecture augmente près d'un métal ou d'un
liquide.
Pour une fréquence plus élevée, les données sont transmises plus
rapidement, la distance de lecture est plus grande, mais les ondes
radio sont plus sensibles aux interférences dues à la présence de
liquide ou de métaux.
La célérité d’une onde électromagnétique dans l’air, notée c, vaut 3×108 m∙s-1.
3. Calculer la longueur d’onde d’une onde radio de fréquence 135 kHz.
l = c / f = 3 108 / (135 103) ~2,2 103 m.
Sur une carte de cantine, l’antenne RFID est réalisée en bobinant un
fil de cuivre autour d’une surface rectangulaire de longueur 6,5 cm et
de largeur 4,5 cm.
4. Calculer le périmètre de la surface rectangulaire.
2 x(6,5 +4,5) = 22 cm = 0,22 m.
5. Calculer le nombre de
tours de fil de cuivre qu’il faut bobiner pour obtenir une antenne
demi-onde pour la fréquence de 135 kHz.
Pour une antenne demi-onde, la longueur de fil d'antenne est 2 fois
plus petite que la longueur d'onde de l'onde radio soit 1,1 103 m.
1,1 103 / 0,22 =5 103.
On admet qu’une onde radio de fréquence 13,56 MHz a une longueur d’onde de 22 m.
6. Proposer un avantage à augmenter la fréquence lorsqu’on utilise la technologie RFID.
Pour
une fréquence plus élevée, les données sont transmises plus rapidement,
la distance de lecture est plus grande, mais les ondes radio sont plus
sensibles aux interférences dues à la présence de liquide ou de métaux.
EXERCICE 4 – B
Rénovation énergétique
Dans les années 1990, un constructeur a livré deux maisons voisines
identiques dont l’une a été rénovée et isolée. Lors du dernier hiver,
la température extérieure est restée pratiquement constante et égale à
0 °C durant plusieurs jours. Après une interruption de chauffage,
l’évolution de la température à l’intérieur des maisons a été
enregistrée pendant deux jours consécutifs, ce qui a permis de tracer
les graphes ci-dessous.
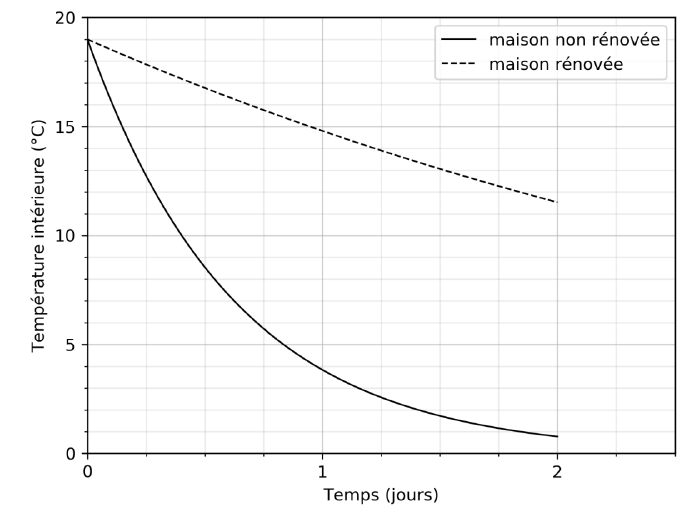
1. Expliquer pourquoi la température intérieure de ces maisons diminue lorsque le chauffage est interrompu.
Il existe un flux thermique de l'intérieur vers l'extérieur, non
compensé par le chauffage. Au bout d'un temps très long, les
températures intérieure et extérieure seront identiques.
La capacité thermique C de l’habitation, rénovée ou non, vaut 60 MJ∙K-1.
2. Estimer, à
partir du graphique, la valeur de la quantité d’énergie échangée avec
l’extérieur par la maison non rénovée durant cette période de deux
jours.
Q = C DT = 60(1 -19) = -1,08 103 MJ.
3. Interpréter le signe du résultat obtenu.
L'intérieur de la maison cède de l'énergie à l'extérieur ( corps froid ).
Le flux thermique F peut s’exprimer par la relation F=C⋅DT/ Dt .
Dans cette relation, la capacité thermique de l’habitation est notée C (en J∙K-1) et DT est la variation de température intérieure de l’habitation (en degrés Celsius) durant la durée Dt (en seconde) du transfert d’énergie.
4. Montrer, en s’appuyant sur une analyse dimensionnelle, que l’unité du flux thermique est le watt (W).
C⋅DT/ Dt s'exprime en J K-1 K s-1 soit J s-1 soit en watt.
5. Vérifier que la valeur du flux thermique moyen durant la première journée sans chauffage pour la maison non rénovée est F=−10,4 kW.
60 106 x (4-19) /(24 x3600)= -1,04 104 W = -10,4 kW.
Pour la maison non rénovée, le flux thermique durant le second jour
sans chauffage est six fois plus faible que durant la première journée.
6. Expliquer pourquoi la valeur du flux thermique diminue au cours du temps.
La différence de température entre l'intérieur et l'extérieur diminue avec le temps.
7. Donner la valeur
approximative des températures intérieures des deux maisons après 15
jours sans chauffage en faisant l’hypothèse que les conditions
météorologiques restent les mêmes durant cette période.
Maison non isolée : température intérieure = température extérieure = 0 °C.
Maison isolée : la température diminue linéairement de 4,2°C par
jour. Au bout de 15 jours la température sera égal à la température
extérieure soit 0 °C.
|
|