Dosage par voie chimique.
La méthode de Fehling est une méthode de dosage par titrage direct d’une solution de
glucose par une solution de liqueur de Felhing contenant des ions cuivre. Le protocole de
dosage de la solution S
0 de glucose injectée dans le réacteur, est donné ci-dessous :
Diluer la solution de glucose S
0 de concentration en quantité de matière C
0 d’un
facteur 5 : soit S
1 cette nouvelle solution de concentration en quantité de matière C
1.
Placer la solution S
1 dans la burette.
Introduire dans un erlenmeyer V
A = 5,0 mL de liqueur de Fehling contenant des ions
cuivre Cu
2+(aq), de concentration C
A = 0,160 mol L
-1
.
Ajouter 40 mL d’eau.
Porter le contenu de l’erlenmeyer à ébullition et y verser goutte à goutte la solution
diluée de glucose S
1 placée dans la burette.
Maintenir l’ébullition entre chaque addition de solution diluée de glucose.
Un
précipité rouge d’oxyde cuivreux se forme et le liquide surnageant bleu se décolore.
On note V
E le volume de solution versée à l’équivalence repérée par une
décoloration complète du liquide surnageant.
Résultat obtenu : V
E = 6,5 mL.
Données fournies par le fabriquant sur la matière première de glucose S
0 :
- formule brute : C
6H
12O
6
- concentration en masse : Cm = 50 ± 2 g·L
-1
- masse molaire du glucose : M = 180 g·mol
-1
L’équation de la réaction support du titrage est :
2 Cu
2+
(aq) + C
6H
12O
6 (aq) + 5 HO
‾ (aq) → Cu
2O (s) + C
6H
11O
7‾ (aq) + 3 H
2O (l)
Les potentiels standards des couples oxydant/réducteur (à 25°C) mis en jeu sont les
suivants :
Cu2+
(aq) / Cu2O (s) E°1 = 1,02 V.
C6H11O7‾ (aq) / C6H12O6 (aq) E°2 = -0,24 V.
B.1. Justifier que la réaction de dosage évolue bien spontanément dans le sens direct. On
la considérera comme totale.
La réaction spontannée a lieu entre le réducteur le plus fort ( le glucose ) et l'oxydant le plus fort ( Cu
2+aq).
B.2. Montrer que la concentration en quantité de matière C1 de la solution S1 se calcule par
la relation :
𝐶1 =
𝐶
𝐴 × 𝑉
𝐴
/ (2 × 𝑉
𝐸).
A l'équivalence :
quantité de matière de glucose : C1 V
E.
quantité de matière d'ion cuivre (II) : C
AV
A.
prendre en compte les coefficients stoechiométriques :
CAVA = 2 C1 VE.
𝐶1 =
𝐶𝐴 × 𝑉𝐴
/ (2 × 𝑉𝐸).
B.3. Calculer les concentrations en quantité de matière C1 et C
0 du glucose dans les
solutions S
1 et S
0.
C1 = 0,160 x 5,0 / (2 x6,5) =0,06154 ~6;2 10
-2 mol / L.
C
0 = 5 C1 =0,3077 ~0,31 mol / L.
B.4. En déduire la concentration en masse Cm de S0.
Cm = 0,3077 x M(glucose) = 0,3077 x 180 =55 g / L.
B.5. Comparer ce résultat aux données fournies par le fabricant 50±2 g/L.
Ecart relatif (55-50) / 50 = 0,10 (10 %).
L'indication du fabricant n'est pas correcte.
Dosage du glucose par une méthode physique.
La méthode physique de dosage du glucose par la mesure de l’indice de réfraction est
utilisée dans des appareils de mesure appelés réfractomètres, qui déterminent l’indice de
réfraction d’une solution à partir de la mesure de l’angle limite de réfraction.
Une goutte d’échantillon de la solution à doser est déposée dans le puits de mesure. Les
rayons de lumière émis par une source passent à travers un prisme en contact avec la
solution.
Le schéma simplifié, pour un rayon incident unique, est donné ci-dessous.
En fonction de l’angle d’incidence i de chaque rayon, celui-ci est réfracté ou seulement
réfléchi. Une lentille fait converger les rayons réfléchis vers un capteur. La séparation entre
la zone éclairée et la zone d’ombre sur le capteur permet de déterminer l’angle d’incidence
pour lequel on a réfraction limite, appelé « angle de réfraction limite » et noté i
lim, de réfraction et de réfraction limite.
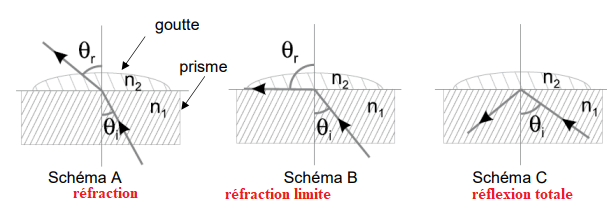 C.2.
C.2. Montrer que dans la situation de la réfraction limite, la relation entre l’angle de
réfraction limite et les indices des milieux est la suivante : sin(i
𝑙𝑖𝑚) =
𝑛
2
/𝑛
1
.
Loi de la réfraction n
1 sin i
1 = n
2 sin i
2.
Réfraction limite :
n1 sin ilim = n2 sin90 = n2.
sin ilim = n2 / n1.
Pour étalonner l’appareil de mesure, une goutte d’une solution de concentration en masse
de glucose connue est déposée sur le prisme pour faire une première mesure. Une
deuxième solution est ensuite employée pour une deuxième mesure.
L’indice de réfraction d’un milieu peut dépendre de la température et de la longueur d’onde
de la lumière. Les valeurs d’indice de réfraction données ci-dessous sont mesurées à une
température de 20 °C et pour un rayonnement monochromatique d’une lampe à vapeur de
sodium, de fréquence 5,09 10
14 Hz.
Données :
- indice de réfraction du verre optique constituant le prisme : n
1 = 1,720 ;
- indice de réfraction pour une solution 1 d’eau distillée : n
0 = 1,333 ;
- indice de réfraction pour une solution 2 de glucose à 40 gL
-1
: n
40 = 1,436
C.3. Déterminer la valeur de l’angle de réfraction limite i
lim_40 pour la solution 2.
sin
ilim_40=
n40 / n1 = 1,436 / 1,720 =0,835 ; ilim_40=56,6 °.
C.4. Montrer que la célérité de l’onde lumineuse émise par la lampe à sodium dans le verre
optique du prisme vaut c
verre = 1,74 10
8 m s
-1
.
c
verre = 3,0 10
8 / n
1 =
3,0 108 / 1,72 = 1,74 108 m s
-1
.