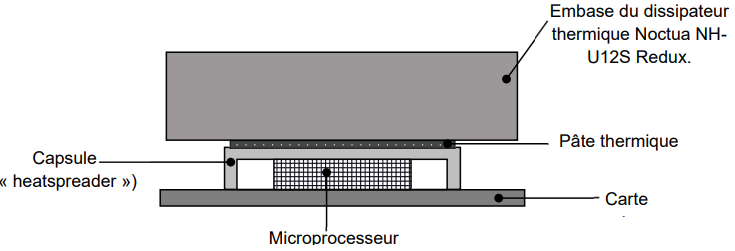
Sur les microprocesseurs présents dans nos ordinateurs sont montés des
dissipateurs thermiques (refroidisseurs passifs ou actifs) qui favorisent
l’évacuation de l’énergie thermique produite au niveau des transistors du
microprocesseur.
 Données
Données : conductivité thermique de la pâte thermique Noctua NT-H1 :
l = 3,0 W·m
-1·K
-1 ;
− dimensions de la capsule en contact avec la pâte thermique : 34,5 mm × 32,0 mm ;
− température de fonctionnement de la capsule du microprocesseur à pleine charge : 72 °C.
La capsule est constituée de cuivre plaqué nickel de très bonne conduction thermique qui
permet de considérer la température de la capsule comme homogène sur tout la surface de
contact avec la pâte thermique ;
− température de l’embase du ventirad : 60 °C.
Dans un premier temps, on étudie la pâte comme siège du transfert thermique.
Q1. Préciser à l’aide d’un schéma simplifié de la situation le sens du transfert thermique. Justifier.
L transfert thermique s'effectue du corps le plus chaud (
capsule du microprocesseur) vers le corps le plus froid ( embase du ventirad ).
Q2. On considère que le transfert thermique s’effectue uniquement par conduction au travers de
la pâte thermique. La valeur du flux thermique fournie par le constructeur pour le Intel core i5 11400F
est de 65 W. Déterminer la valeur de la résistance thermique R
th de la pâte thermique.
Flux thermique = Différence des températures / R
th .
Rth =(72 -60) / 65=0,18 K W-1.
Q3. En déduire l’épaisseur e de la pâte thermique. Commenter.
R
th = e /(
lS) ; e =
l S Rth =3,0 x34,5 10-3 x32,0 10-3 x0,18=6,0 10-4 m = 0,60 mm. (épaisseur très faible).
On s’intéresse désormais à la partie haute du ventirad.
À la suite d’une utilisation intense du microprocesseur, on suppose que le ventirad a une
température T homogène de 60 °C (valeur issue du protocole d’essai de Noctua).
La température extérieure T
air est supposée constante et égale à 22 °C.
Le flux thermique
Fth associé au transfert thermique entre le système de dissipation à la température
T et l’air à la température Tair est donné par la loi de Newton :
Fth (t) = h × S (T
air –T(t))
avec h le coefficient de transfert thermique surfacique et S la surface d’échange.
Q4. La vitesse de rotation du ventilateur est asservie à la température du ventirad. Déterminer
qualitativement le sens de variation de h lorsque le débit d’air produit par le ventilateur augmente.
Le flux thermique étant constant, h doit diminuer.
On souhaite étudier le refroidissement passif du ventirad (microprocesseur et ventilateur éteints)
lorsqu’on l’arrête en considérant que la température est homogène sur l’ensemble du dispositif.
Q5. Montrer, en appliquant le premier principe de la thermodynamique au ventirad, que la
température T(t) des éléments de dissipation du ventirad vérifie l’équation différentielle suivante :
dT(t)/
dt = − hS
/C
(T(t)-Tair)
avec C, la capacité thermique du dispositif de refroidissement.
Variation de l'énergie interne : Q +W = Q ( le travail étant nul ).
DU =Q = C
DT.
D'autre part :Q =
Fth (t) Dt=
h × S (Tair –T(t))Dt.
C DT = h × S (Tair –T(t))Dt.
DT / Dt= h × S /C (Tair –T(t))= -h S / C(T(t)-Tair)
En prenant Dt petit : dT(t)/
dt = − hS
/C (T(t)-Tair).
Q6. Par un raisonnement d’homogénéité mené sur l’équation différentielle ci-dessus, déterminer
l’unité de la grandeur C/(
hS).
hS
/C possède la dimension de 1 /dt soit s-1.
C /(hS) a la dimension d'un temps.
.
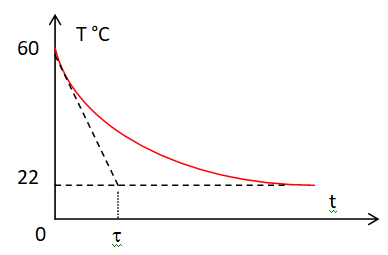
Q7. Représenter sur votre copie l’allure de l’évolution de la température des éléments de
dissipation du ventirad. On précisera les valeurs de la température initiale et finale.
 Q8.
Q8. En utilisant l’équation différentielle, discuter de l’influence de la grandeur C
/ (h S) sur la pente à
l’origine de la courbe T(t). Proposer une interprétation de la grandeur C
/(h S).
C /(hS) est la constante de temps notée
t ; elle donne une indication sur la rapidité d'évolution du système.
Si C
/ (h S) diminue, la valeur absolue de la pente de la tangente à
l’origine de la courbe augmente.