Valoriser l'énergie cinétique d'une rame de métro, bac Métropole 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . . .. .. ...... ... Les transports publics de proximité (tramway, métro, bus) sont caractérisés par une succession de petits trajets et d’arrêts fréquents. Pour l’optimisation de la dépense énergétique, il est intéressant de récupérer l’énergie cinétique du véhicule durant une phase de freinage afin de la restituer pour aider au redémarrage. Il existe plusieurs dispositifs permettant de stocker de l’énergie électrique dans le contexte des systèmes de transport.  L’exemple de la rame du métro parisien de la ligne 14.  La trajectoire de la rame entre les stations Châtelet et Gare-de-Lyon est considérée comme rectiligne et horizontale. La masse m d’une rame avec passagers du métro de la ligne 14 est 1,4×105 kg. 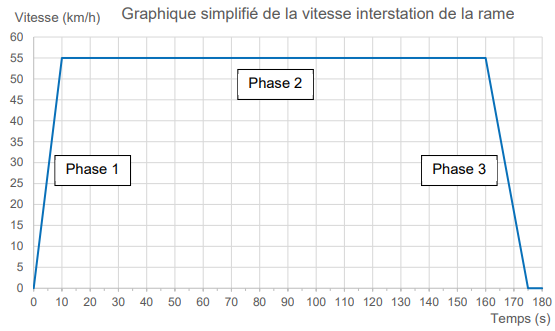Q1. Caractériser le mouvement de la rame, avec les termes adaptés, pour les trois phases du graphique représentant la vitesse de la rame en fonction du temps. Phase 1 : mouvement uniformément accéléré. Phase 2 : mouvement uniforme ( norme de la vitesse constante). Phase 3 : mouvement uniformément décéléré.  Q2. Déterminer l’expression puis la valeur de la puissance moyenne maximum récupérable Précup lors de la phase de freinage. Commenter cette valeur par comparaison à une autre situation concrète du quotidien. Variation d'énergie cinétique : | ½mv2 |=0,5 x 1,4 105 x(55 / 3,6)2 =1,6 107 J. Puissance correspondante = énergie / durée = 1,6 107 / 15 =1,1 105 W. Valeur très grande par rapport à la puissance des appareils électriques courants d'une maison.  Q3. Déterminer si la puissance moyenne minimale P nécessaire au démarrage de la rame (phase 1) est supérieure ou inférieure à la valeur Précup ? Justifier la réponse. Variation d'énergie cinétique : | ½mv2 |=0,5 x 1,4 105 x(55 / 3,6)2 =1,6 107 J. Puissance correspondante = énergie / durée = 1,6 107 / 10 =1,6 106 W. La puissance nécessaire au démarrage est supérieure à la puissance récupérable lors du freinage. La valeur de l’énergie maximale récupérable lors du freinage est d’environ 4,5 kWh. Q4. À partir des informations du tableau ci-dessus présentant des données des systèmes de stockage d’énergie, choisir le système de stockage le moins encombrant. Supercondensateur : (0,93 dm3 par élément) ; énergie d'un élément : 4,37 Wh. Il faudrait : 4,5 103/ 4,37 ~ 1030 éléments. Volume total : 1030 x 0,93 = 958 dm3. Batterie (1,51 dm3 par élément stockant 162 Wh) Il faudrait : 4,5 103/ 162 ~ 28 éléments. Volume total : 28 x 1,51 ~ 42 dm3. Volant d'inertie (165 dm3 stockant 400 Wh). Il faudrait : 4,5 103/ 400 ~ 12 éléments. Volume total : 12 x 165 ~ 1980 dm3. Les batteries sont les moins encombrantes. Q5. En pratique, c’est le volant d’inertie qui est privilégié et ce, malgré son encombrement. En s’appuyant sur les données à disposition, proposer une explication à ce choix. Le rendement de ce volant ( 88 %) est supérieur à celui des batteries ( 80 %).  Q6. Sélectionner parmi les quatre schémas ci-dessous celui qui représente correctement les vecteurs vitesse  et accélération  d’un point A de la périphérie du volant d’inertie en rotation lorsque la vitesse de rotation du rotor diminue. Justifier. 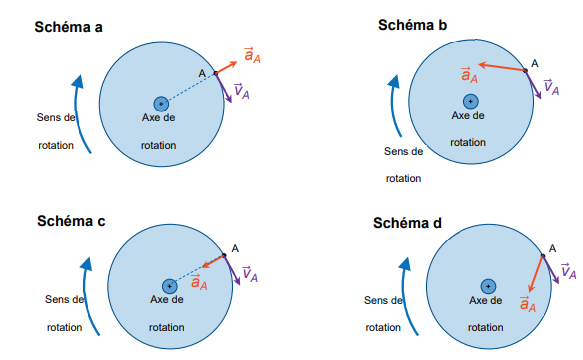Schéma c : lors d'une diminution de la vitesse, l'accélération est centripète, dirigée vers l'axe. Le cylindre du SSI a un rayon R = 35 cm et tourne à une vitesse constante. La valeur de la vitesse du point A est alors vA = 280 m⋅s-1.  Q7. Exprimer et calculer la valeur de la composante normale an du vecteur accélération dans le repère de Frenet. Comparer cette valeur à celle, supposée connue, de l’intensité de la pesanteur. Commenter. an = v2 / R =2802 / 0,35 =2,2 105 m s-2, valeur très supérieure à 9,81 m s-2.

menu