On étudie le vol d’un parapente et de son pilote assimilé à un point matériel G
situé au centre de masse du système {pilote + parapente}. Un vol droit équilibré est un vol
au cours duquel la trajectoire est rectiligne et sans variation de vitesse. L’air environnant
est supposé immobile.
Étude cinématique
On observe un parapente en vol droit équilibré. On se demande s’il s’agit d’une
voile d’école ou de compétition.
Le mouvement du système est contenu dans un plan vertical muni du repère.
Depuis le sol, on filme le mouvement. Puis on pointe les positions successives de G.

Les coordonnées cartésiennes de G(x,y), dans le repère , obtenues après
modélisation s’expriment en fonction du temps :
x(t)= = 11,0 × t ; y(t) = −1,1 ×t.
Dans ces relations, x(t) et y(t) sont exprimés en mètres et t en secondes
1. Déterminer les composantes du vecteur vitesse du système puis la valeur de la vitesse
du système en m·s
-1 puis en km·h
-1 du parapentiste.
La vitesse est la dérivée par rapport au temps de la position.
v
x(t) = 11,0 et v
y(t) = -1,1.
v =(11,0
2 +(-1,1)
2)
½ ~11,1 m/s ou 11,1 x3,6 ~40 km /h.
2. Vérifier, à partir des résultats de la question précédente, la nature rectiligne uniforme
du mouvement. En déduire son vecteur accélération.
La valeur de la vitesse étant constante, le mouvement est uniforme.
t = x / 11 ; repport dans y(t) :
y = -1,1 x /11 =-0,1 x, fonction linéaire ( le mouvement est rectiligne).
Le vecteur accélération est nulle ( première loi de Newton).
3. Calculer l’angle de plané
a.
tan
a = |y| /x=1,1/11=0,1 ;
a=5,7 °.
Étude dynamique
Au cours du mouvement d’un corps dans un fluide, il apparaît deux forces de contact
qu’exerce le fluide sur le corps :
- la traînée T, de direction identique au vecteur vitesse mais dont le sens est opposé
au sens du vecteur vitesse,
- la portance F, dont la direction est perpendiculaire à celle du vecteur vitesse et
dans le plan (𝑥Oy).
Les forces qui s’appliquent sur le système {pilote + parapente} sont le poids P, la traînée T et la portance F.
La masse de l’ensemble du système est m = 87,7 kg.
Le parapentiste effectue un vol droit équilibré avec une vitesse par rapport au sol de
v= (11 ± 1) m·s
-1 faisant un angle
a = 5,7 ° par rapport à l’horizontale.
Données : intensité du champ de pesanteur terrestre : g = 9,80 m·s
-2
expression de l’intensité de la traînée T= 0,5
r v
2 S Cx
avec
r : masse volumique de l’air à l’altitude de vol = 1,14 kg·m
-3
v : vitesse du corps en m.s
-1 ;
S : surface de référence en m
2 : la voile du parapente étudié a une surface de
référence de 22,6 m
2
.
Cx : le coefficient de traînée, sans unité, reflète l’aérodynamisme dépendant de la
forme. Il dépend de la forme du corps en mouvement dans le fluide.
4. À l’aide de la deuxième loi de Newton, obtenir une relation entre T, m, g et
a. On
pourra utiliser la direction de la trajectoire comme axe de projection.
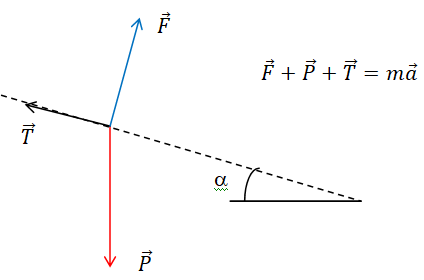
-T +mg sin
a = ma.
Le mouvement étant rectiligne uniforme, l'accélération est nulle.
T = mg sin
a.
5. En déduire le coefficient Cx en fonction de m, g,
a,
r, v et S. Présenter le résultat
accompagné de son incertitude-type associée.
T= 0,5 r v2 S Cx=mg sin a.
Cx = mg sin a /(0,5 r v2 S)= 87,7 x9,80 x sin(5,7) / (0,5 x1,14 x11,12 x22,6)=0,054.
u(Cx) = 2 Cx (u(v) / v)=2x0,054 x1 /11 ~0,01.
Cx = 0,05 ±0,01.
6. Déterminer la forme de la voile et vérifier que le résultat de la mesure est en accord
avec la valeur de référence.
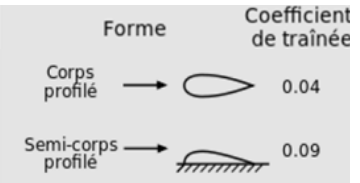
(0,05-0,04) / 0,01 = 1 < 3.
La voile est un corps profilé.