Concours
externe adjoint technique de recherche et de formation principal
Poitiers 2016.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
En
première approximation sa trajectoire autour du soleil peut être
considérée comme circulaire. Sa distance du soleil varie de 0,31 u a à
0,47 ua et sa vitesse , qui vaut en moyenne 47 km /s, varie de 39 à 59
km /s.
Rayon de Mercure : R =2440 km.
1 ua = 1,5 1011 m.
Etude de la trajectoire de
Mercure.
1.
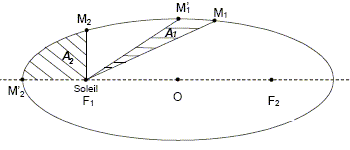
Enoncer la première loi de Kepler. Représenter, sans souci
d'échelle,l'allure de la trajectoire de Mercure autour du soleil. Faire
apparaître la position du soleil et le demi-grand axe de l'orbite.
Le soleil est l'un des foyers de l'ellipse.
 2.
Montrer par un calcul simple que le demi-grand axe vaut 0,39 ua.
2.
Montrer par un calcul simple que le demi-grand axe vaut 0,39 ua.
(0,47 +0,31) / 2 = 0,39 ua.
3. Enoncer la
seconde loi de Kepler. Appliquer cette loi pour déterminer dans quelle
partie de sa trajectoire Mercure atteint sa vitesse de 39 km /s.
Justifier.
Deuxième
loi ou loi des aires : le
mouvement de chaque planète est tel que le segment de droite reliant le
soleil et la planète balaie des aires égales pendant des durées égales.
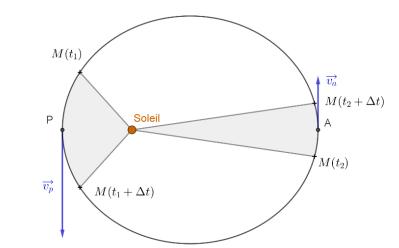
Les aires hachurées sont égales.
La distance M(t1) M (t1+Dt)
est supérieure à la distance M(t2) M (t2+Dt).
Donc la vitesse de
Mercure au point le plus proche du soleil est plus grande que la
vitesse au point le plus éloigné.
La troisième loi de Kepler s'écrit T2/a3 = k avec
k = 2,9 10-19 SI pour le système solaire.
4.
Donner la signification de T et a pour Mercure. Justifier que cette
planète parcourt l'ensemble de son orbite autour du soleil en un peu
moins de trois mois.
T : période de révolution de Mercure autour du Soleil.
a : demi grand-axe de l'ellipse.
a = 0,39 x 1,5
1011 = 5,85 1010
m.
T2 = ka3 =2,9 10-19 x(5,85 1010)3
=5,8 1013.
T =7,6 106 s ou 88 jours.
|
...
|
....
|
Etude de la
trajectoire de Messenger.
Satellisée autour de Mercure, cette sonde effectue des orbites avec une
période TS
=8,00 heures. Lors de son passage au plus près de la surface de la
planète, à l'altitude h = 200 km, la sonde possédait une accélération a
= 3,15 m s-2. On supposeraa que cette accélération est due
uniquement à l'attraction de Mercure.
On note m la masse de la sonde et M la masse de Mercure et R le rayon
de Mercure.
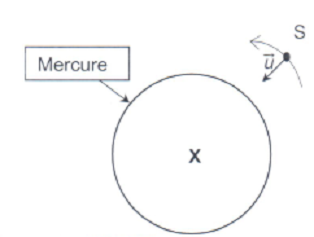
5.
Reproduire le schéma en y faisant apparaître R, r, le vecteur force
gravitationnelle exercée par Mercure sur la sonde, le vecteur vitesse
de la sonde ainsi que son vecteur accélération.
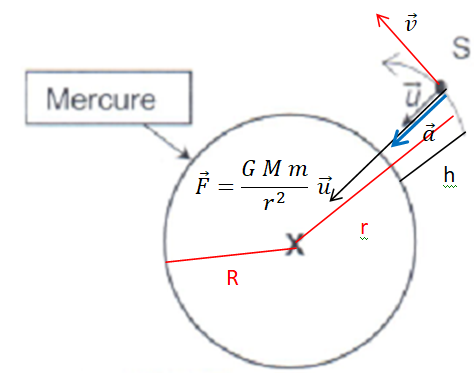
6.
Enoncer la seconde loi de Newton, puis l'appliquer à Messenger dans le
référentiel mercurocentrique considéré galiléen. En déduire
l'expression du vecteur accélération.
Dans un référentiel galiléen, la somme vectorielle des forces
extérieuresappliquées au système est égale au produit de la masse du
système par son vecteur accélération.
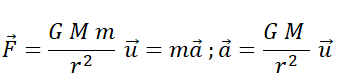
7. En déduire M,
masse de Mercure.
M = a r2 / G =3,15 x[(2440 +200)103]2
/ (6,67 10-11)= 3,29 1023 kg.
8.
Appliquer la troisième loi de Kepler au mouvement de la sonde ;
calculer la valeur du demi-grand axe de son orbite. Expliquer pourquoi
la trajectoire de la sonde ne peut pas être considérée comme circulaire.
a3 = TS2 GM / (4p2).
a3 =(8,00 x3600)2 x 6,67 10-11
x3,29 1023/ (4 x3,142)=4,61 1020.
a =7,72 106 m = 7,72 103 km.
Cette valeur étant très supérieure à r = 3640 km, la trajectoire de la
sonde n'est pas circulaire.
|
|