Eclipse solaire du 10 juin, lunette astronomique, bac Polynésie 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Exercice B ( 5 points).   La lunette astronomique. La figure suivante présente de façon simple la lunette de Galilée. 1. Associer aux lentilles L1 et L2 les termes objectif et oculaire. L1 plus proche de l'objet lointain est l'objectif. L2 proche de l'oeil est l'oculaire. 2. Pour la lentille L1, donner le nom du point P où les rayons se croisent. L'image d'un objet à l'infini est dans le plan focal image de l'objectif.. 3. La lunette commerciale utilisée est afocale. Positionner le foyer principal objet F2 et le foyer principal image F '2 de la lentille L2. Le foyer principal objet de L2 est confondu avec le foyer principal image de l'objectif L1. 4. Indiquer comment le rayon issu de Boo passant par le centre optique O1 traverse la lentille L1. Un rayon passant par le centre optique de la lentille L1 n'est pas dévié. 5. Construire l'image intermédiaire A1B1.   6. Donner les deux caractéristiques de l'image A1B1. Cette image est réelle et inversée par rapport à l'objet. 7. Construire l'image définitive. Représenter le faisceau de rayons lumineux issu de l'objet Boo, passant par les bords de la lentille L1.   ... .... Grossissement de la lunette asronomique. 9. Positionner l'angle a' sous lequel est observée l'image définitive de la lune à travers la lunette. 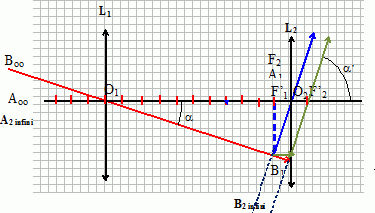Le grossissement G a pour expression G = a' / a. 10. Démontrer que G = f '1 / f '2. Triangle O2F'1B1 : tan a' = A1B1/O2F2 ~ a' . L'angle étant petit , on confond la tangente avec l'angle en radian. Triangle O1F'1B1 : tan a = A1B1/O1F1 ~ a . Grossissement G = a' / a =O1F1 /O2F2 =f '1 / f '2. 11. Calculer G si f '1 = 66 cm et f '2=9 mm. G = 66 / 0,9 ~73. 12. Comparer avec l'indication du fabriquant " grossissement maximal  x 73". La valeur trouvée est en accord avec cette indication. Une eclipse solaire a lieu lorsque la lune se place entre la terre et le soleil et que les trois sont alignés. 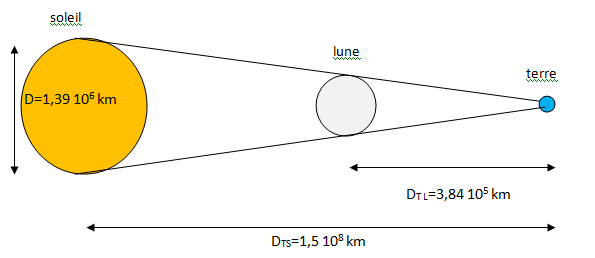Dans le cas d'une éclipse totale, la lune ayant un diamètre 400 fois plus petit que celui du soleil, mais étant aussi 400 fois plus proche de la terre, leurs deux diamètre coîncident et le recouvrement sera presque parfait. Ce type d'éclipse  est très rare. 13. Montrer que ces deux informations , pour déterminer le diamètre de la lune, donne des valeurs similaires. On note d le diamètre de la lune. D'après le schéma : d / DTL = D / DTS ; d = D DTL/ DTS  =1,39 106 x 3,84 105 / (1,5 108) ~3,6 103 km. D'après le texte : d = D / 400 = 1,39 106 / 400 ~3,5 103 km. Ecart relatif : ( 3,6 -3,5) / 3,5 ~0,03 ( 3 %). Ces deux valeurs sont similaires.

menu