Un tracteur gravitationnel pour dévier un astéroïde, bac Polynésie 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Exercice 2 ( 5 points).   Etude de la déviation d'un astéroïde. 1. Représenter sans souci d'échelle, la force de gravitation exercée par l'engin spatial E sur l'astéroïde A, tous deux considérés comme des points matériels, lorsqu'ils se trouvent à la distance d =AB l'un de l'autre. 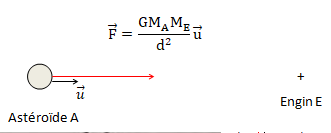Cette interaction a lieu pendant une durée Dt faible devant la période orbitale de l'astéroïde. Pendant cet intervalle de temps, la trajectoire de l'astéroïde est supposée quasi-rectiligne et l'engin se maintient à une distance d constante de l'astéroïde. 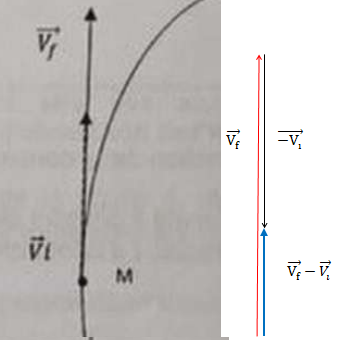On a représenté ci-dessous une portion  de la trajectoire de l'astéroïde ainsi que sa vitesse initiale Vi  en un point M de sa trajectoire sans présence de l'engin spatiel puis le vecteur vitesse Vf de l'astéroïde juste après l'interaction en présence de l'engin spatial. 2. Représenter le vecteur variation de vitesse résultant de l'interaction avec l'engin spatial et qui permet de le dévier de sa trajectoire. 3. En déduire la direction privilégiée dans laquelle  les astronomes doivent placer l'engin spatial pour dévier l'astéroïde de sa trajectoire initiale en choisissant parmi les propositions suivantes : Dans la direction de DV : oui, la vitesse finale augmente, donc le rayon de l'orbite croït.  Perpendiculaire à DV :non. La force de gravitation exercée par le soleil  est très supérieure à FE/A.  Quelconque : non..   Application à la direction d'Apophis. Masse d'Apophis M = 4 1010 kg. Masse de E : m = 5 103 kg ; distance d = 240 m. 4. Donner l'expression de la norme de la force FE/A et calculer sa valeur. FE/A = G M m / d2 =6,67 10-11 x 4 1010 x 5 103 / 2402=0,23 ~0,2 N. Soit Dt la durée pendant laquelle il faut appliquer cette force pour obtenir la variation de vitesse DV voulue. 5. En appliquant la seconde loi de Newton à Apophis, dans le référentiel héliocentrique, montrer que Dt = DVd2 / (G m). Selon un axe tangentiel à la trajectoire, orienté dans le sens du mouvement, la seconde loi de Newton conduit à : F = G M m / d2 = M DV / Dt. G  m / d2 =  DV / Dt. Dt = DVd2 / (G m). Les scientifiques ont estimé qu'il pourrait suffire d'augmenter la norme du vecteur vitesse de l'astéroïde de 2 10-6 m /s au niveau de l'aphélie pour éviter la terre. 6 .  Montrer que, dans ces conditions, Dt ~ 4 jours. Dt = 2 10-6 x 2402 / (6,67 10-11 x 5 103) =3,45 105 s ~96 heures ~4 jours. ... .... L'utilisation du tracteur gravitationnel engendre une augmentation du rayon de la trajectoire de l'astéroïde. Cette modification entraîne une augmentation de la période de révolution T de l'astéroïde autour du soleil d'environ 15 minutes, ce qui évitera l'impact avec la terre. Rayon de la trajectoire d'Apophis R = 1,37961 1011 m. Masse du soleil M = 1,98892 1030 kg. T = 323,442 jours sans la présence du tracteur. G = 6,67408 10-11 N m2kg-2. On considère que l'astéroïde évolue autour du soleil selon un mouvement uniforme quasi-circulaire de rayon R. 7. Etablir la troisième loi de Kepler pour Apophis dans le référentiel héliocentrique. 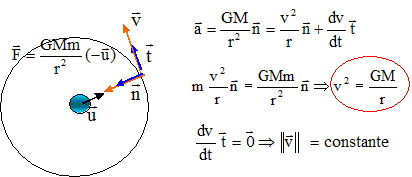L'astéroïde décrit la circonférence 2pr à la vitesse v en T seconde. 2 p r = vT ; 4 p2 r2 = v2 T2 =GM / r T2. T2 / r3 = 4 p2 /(GM). 8. Calculer la valeur de la période de révolution T ' d'apophis après l'utilisation du tracteur. T ' = T + 15 x 60 = 323,442 x24 x3600 +15 x 60 =2,7945 107 +900 =2,794629 107 s. 9. Calculer la valeur du nouveau rayon de la trajectoire R ' et en déduire la valeur de l'augmentation DR en mètre de rayon de cette trajectoire. T2 / R3 = T '2 / R '3 ; R ' 3 =( T ' / T )2 R3. R ' = ( T ' / T )2 / 3 R. ( T ' / T )2 / 3  =2,794629 107  / (2,794539 107 ) ~1,0000215. R ' = 1,0000215 x 1,37961 1011 =1,37964 1011 m. DR  =(1,37964 -1,37961) 1011 =2.9660 106 m.

menu