Mathématiques,
géométrie, Bac Polynésie
2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
L’espace est rapporté un repère orthonormal où l’on considère :
les points A(2 ; −1 ; 0) B(1 ; 0 ; −3), C(6 ; 6 ; 1) et E(1 ; 2 ; 4);
Le plan P d’équation cartésienne 2x − y − z +4 = 0.
1. a. Démontrer que le triangle ABC est rectangle en A.
AB 2 =(1-2) 2 +(0-(-1)) 2+(-3-0) 2 =11.
AC2 =(6-2)2 +(6-(-1))2+(1-0)2 =66.
BC2 =(6-1)2 +(6-0)2+(1-(-3))2 =77.
BC2 =AC2 +
AB2 .
b. Calculer le produit scalaire suivant puis les longueurs BA et BC.
c. En déduire la mesure en degrés de l’angle ABC arrondie au degré.
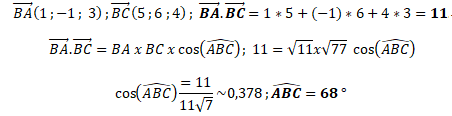 2. a. 2. a. Démontrer que le plan P est parallèle au plan (ABC).
 b.
b. En déduire une équation cartésienne du plan (ABC).
2x − y − z +d = 0.
A(2 ; -1 ;0) appartient au plan ABC : 2*2-(-1)-0+d = 0 ; d = -5.
2x − y − z -5= 0.
c. Déterminer une représentation paramétrique de la droite D orthogonale au plan
(ABC) et passant par le point E.
Coordonnées d'un vecteur directeur de la droite (D) : (2 ; -1 ; -1).
Par suite x = 2t+x E =2t+1.
y = -t+y E =-t+2.
z = -t+z E = -t+4 avec t réel.
d. Démontrer que le projeté orthogonal H du point E sur le plan (ABC) a pour
coordonnées (
4 ;
1
/2
;
5/
2 )
.
Le point H appartient au plan (ABC) et à la droite D.
2x H-y H-z H-5=0.
x H = 2t+1 ; y H = -t+2 ; z H = -t+4.
2(2t+1) -(-t+2)-(-t+4)-5 = 0.
6t= 9 t = 1,5.
x H =2 *1,5+1 = 4 ; y H =-1,5 +2 = 0,5 ; z H = -1,5 +4 = 2,5.
3. On rappelle que le volume d’une pyramide est donné par V =
1
/3
Bh où B désigne l’aire
d’une base et h la hauteur de la pyramide associée à cette base.
Calculer l’aire du triangle ABC puis démontrer que le volume de la pyramide à ABCE
est égal à 16,5 unités de volume.
Aire du triangle ABC : AB x AC / 2 = 11 ½ x66 ½ / 2 =5,5 x6 ½.
h = HE =[(1-4) 2+(2-0,5) 2+(4-2,5) 2] ½ =13,5 ½=(27 /2) ½ = 3* (3 /2) ½.
V= 5,5 x6½x3 *(3/2)½ / 3=5,5 x3=16,5 unités de volume.
|
...
|
....
|
On
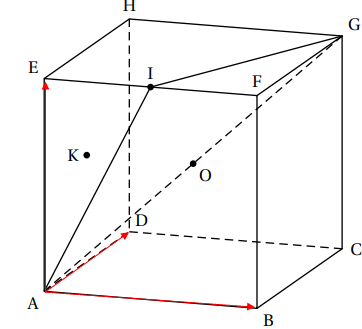
considère le cube ABCDEFGH d’arête de longueur 1.
L’espace est muni du repère orthonormé.. Le point I est le milieu du
segment [EF], K le centre du carré ADHE et O le milieu du segment [AG].
Le but de l’exercice est de calculer de deux manières différentes, la distance du point B au plan
(AIG).
Partie 1. Première méthode
1. Donner, sans justification, les coordonnées des points A, B, et G.
A(0 ; 0; 0) origine du repère.
B(1 ; 0 ; 0) ; G( 1 ; 1 ; 1).
On admet que les points I et K ont pour coordonnées I(
1
/2
; 0 ; 1)
et K(
0 ;
1/
2
;
1/
2 )
.
2. Démontrer que la droite (BK) est orthogonale au plan (AIG).
Coordonnées d'un vecteur directeur de la droite (BK) : ( -1 ; 0,5 ; 0,5) ou encore (2 ; -1 ; -1)..
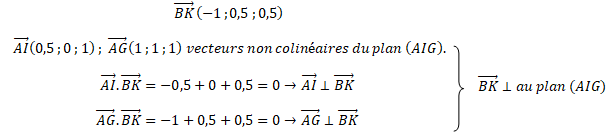
3. Vérifier qu’une équation cartésienne du plan (AIG) est : 2x − y − z = 0.
-x +0,5y +0,5z +d=0
A(0 ; 0 ; 0) appartient à ce plan; par suite d = 0.
-x+0,5y +0,5z = 0 soit en multipliant par -2 : 2x-y-z=0.
4. Donner une représentation paramétrique de la droite (BK).
x = -t +xB =-t+1.
y = 0,5 t +yB = 0,5 t.
z = 0,5 t+zB = 0,5 t.
5. En déduire que le projeté orthogonal L du point B sur le plan (AIG) a pour coordonnées
L
(1
/3
;
1/
3
;
1
/3 ).
L appartient au plan (AIG) et à la droite (D) :
2xL-yL-zL=0.
xL=-t+1 ; yL=0,5t ; zL=0,5 t.
2(-t+1)-0,5t -0,5t = 0
3t =2 ; t = 2 /3.
xL = -2/3 +1=1/3 ; yL = 0,5 x2/3 = 1 /3 ; zL = 0,5 x2/3 = 1 /3.
6. Déterminer la distance du point B au plan (AIG).
BL = [(1/3-1)2+(1/3)2+(1/3)2 ]½ =(6 /9)½ =( 2 /3)½.
Partie 2. Deuxième méthode
On rappelle que le volume V d’une pyramide est donné par la formule V =
1
/3
×b ×h, où b est
l’aire d’une base et h la hauteur associée à cette base.
1. a. Justifier que dans le tétraèdre ABIG, [GF] est la hauteur relative à la base AIB.
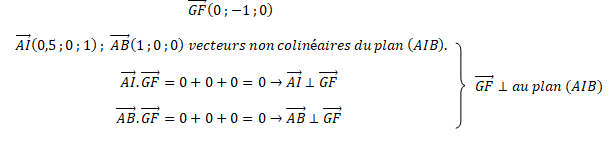
b. En déduire le volume du tétraèdre ABIG.
h = GF = 1.
Base = aire du triangle AIB= 0,5 x aire d'une face du carré = 0,5.
V = 1 x0,5 / 3 = 1 / 6 unité de volume.
2. On admet que AI = IG = 5½ /
2
et que AG =3½.
Démontrer que l’aire du triangle isocèle AIG est égale à 6½/
4
unité d’aire.
2 x aire du triangle rectangle AOI = 0,5 AG xOI.
O( ½xG ; ½yG ; ½zG) soit (0,5 ; 0,5 ; 0,5).
OI =(02 +0,52 +0,52)½ = 1/ 2½ .
Aire du triangle AIG =0,5 x3½x1 / 2½=3½ /(2 *2½)=6½ / 4 unités d'aire.
3. En déduire la distance du point B au plan (AIG).
Volume du tétraèdre ABIG = 1 /3 Aire du triangle AIG x BL =1 / 3 x 6½ /4 xBL=1/ 6.
BL = 2 / 6½ = 2½ x2½ / (2½x3½) =( 2 /3)½.
|
|