Vol d'une mongolfi�re, bac M�tropole 09 / 2021.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts.


.
.
.. ..
......


...
Les objectifs de cet exercice sont :
- de d�terminer la masse totale qu’il est possible d’embarquer dans la montgolfi�re ;
- de trouver l’autonomie de vol maximale possible avec la montgolfi�re.
On �tudie dans cet exercice une enveloppe en nylon de mod�le � M-77 � de 0,1 mm d’�paisseur, de volume V = 2 200 m3, � laquelle on accroche une nacelle de mod�le � C-1 �, de masse m = 56 kg. La nacelle est capable d’embarquer jusqu’� trois personnes ainsi que quatre bonbonnes pesant chacune 40 kg et contenant 20 kg de propane chacune.
Donn�es :  surface de l’enveloppe du ballon : S = 847 m2 ;  masse par unit� de surface de l’enveloppe en nylon : rnylon = 65 g�m–2 ; constante du gaz parfait : R = 8,314 J�mol–1 �K–1 ;  masse molaire de l’air : Mair = 29,0 g�mol–1.

1. D�termination de la masse totale qu’il est possible d’embarquer dans la montgolfi�re.
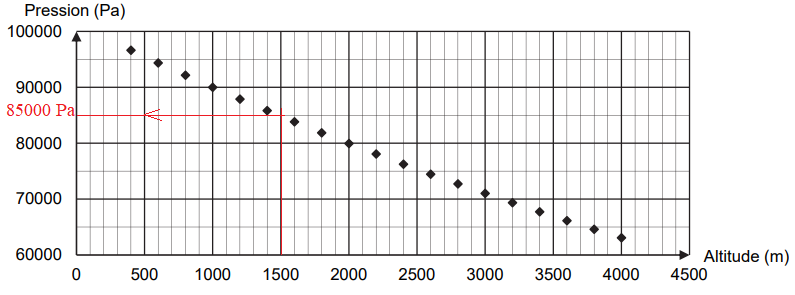
 Au cours d’un vol, la montgolfi�re se trouve � une altitude de 1,5 km. On consid�re que la pression p � l’int�rieur du ballon est �gale � la pression � l’ext�rieur du ballon. La figure suivante pr�sente l’�volution de la pression de l’air en fonction de l’altitude. L’air est consid�r� comme un gaz parfait. Le br�leur n’est pas actionn� au moment o� on �tudie le syst�me.

1.1. �tude du syst�me � ballon �.
 1.1.1. � l’aide de l’�quation d’�tat du gaz parfait, exprimer la masse volumique de l’air contenu dans le ballon  en fonction de la pression P, Mair, R et T, la temp�rature de l’air contenu dans le ballon.
PV = n R T ; n = mair / Mair ; rair = mair / V.
PV = mair / Mair RT ; P = mair / V R T / Mair  = rair R T / Mair ;
 rair = P Mair / (RT).
1.1.2. Montrer que la valeur de la masse volumique de l’air contenu dans le ballon lorsque le ballon est � une altitude de 1,5 km est de l’ordre de 0,8 kg�m–3. On suppose que la temp�rature de l’air � l’int�rieur du ballon � l’instant o� on �tudie le syst�me est � 373 K.
rair = 85 000 x29,0 10-3 /(8,314 x373) =0,795 ~0,8 kg�m–3.

 1.2. �tude du syst�me � montgolfi�re �.
 On suit le d�placement du centre de masse G de la montgolfi�re. On se place dans le r�f�rentiel terrestre suppos� galil�en muni d’un rep�re d’espace. L’origine au point O est au niveau du sol, au point de d�collage de la montgolfi�re.
On consid�re qu’il s’exerce seulement deux forces sur le syst�me {montgolfi�re} compos� de la nacelle, de son chargement et du ballon : - le poids P ; - la pouss�e d’Archim�de qui mod�lise l’action de l’air sur le ballon : PA  = rext � V � g  o� rext repr�sente la masse volumique de l’air ext�rieur et V repr�sente le volume total de la montgolfi�re, dont on consid�re qu’il est �gal au volume du ballon. On consid�re que la masse d’air pr�sente dans le ballon est constante et que la montgolfi�re, de masse totale m, reste immobile. � la temp�rature locale et � l’altitude du vol de 1,5 km, la masse volumique de l’air ext�rieur au ballon vaut 1,06 kg�m–3 tandis que la masse volumique de l’air � l’int�rieur du ballon vaut 0,80 kg�m–3.
1.2.1. Repr�senter les deux forces s’exer�ant sur la montgolfi�re dans le cas o� elle est immobile dans le r�f�rentiel terrestre, sans souci d’�chelle en utilisant le syst�me d’axes de la figure. Justifier.
La mongolfi�re est immobile : le poids et la pouss�e d'Archim�de se compensent.
Poids, verticale vers le bas ; pouss�e, verticale vers le haut.
 1.2.2. Donner l’expression vectorielle du poids P de la montgolfi�re.
1.2.3. �tablir l’expression vectorielle de la pouss�e d’Archim�de PA .

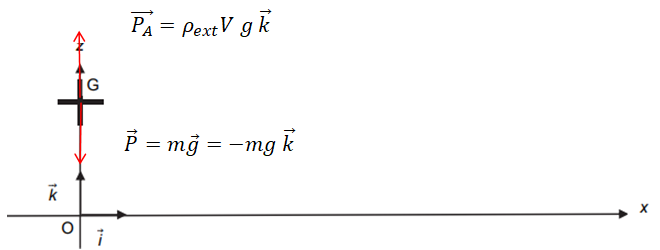1.2.4. En d�duire la masse totale embarqu�e dans la nacelle � cette altitude. Commenter.
P = PA ; rext � V = m .
m = 1,06 x 2200 =2332 kg.
Masse nacelle : 56 kg.
Masse enveloppe : 847 x0,065 ~ 55 kg.
Masse d'air contenue dans le ballon : 0,80 x 2200 =1760 kg.
Masse embarqu�e : 2332 -56-1760 -55 ~461 kg.
Cela correspond � :
la masse des 4 bouteilles de gaz : 4 x(40+20) = 240 kg.
et � la masse des trois personnes : 3 x70 = 210 kg.
.

...
....

 2. D�termination de l’autonomie maximale de vol de la montgolfi�re.
 En r�alit�, la montgolfi�re ne reste pas � une altitude constante. Son altitude varie autour d’une altitude moyenne, au gr� de l’actionnement du br�leur par le pilote. L’utilisation du br�leur est n�cessaire pour maintenir une altitude moyenne constante. On consid�re que la montgolfi�re est en vol, stabilis�e � une altitude moyenne de 1,5 km. La temp�rature ext�rieure est Text = 278 K au cours d’un vol. On cherche � �tablir le bilan �nerg�tique entre le syst�me {air � l’int�rieur de l’enveloppe + enveloppe} et le milieu ext�rieur.
2.1. Nommer les trois modes de transferts thermiques. Caract�riser qualitativement ces trois modes.
Rayonnement ( du soleil dans l'espace), convection ( mouvement des mol�cules dans un fluide), conduction (�change avec contact)..
La figure suivante pr�sente les transferts thermiques qui ont lieu entre le syst�me {ballon} et le milieu ext�rieur.
 On rappelle que le ballon repr�sente l’enveloppe en nylon et l’air contenu � l’int�rieur. En r�gime stationnaire, la montgolfi�re est en �quilibre thermique.

2.2. Etablir une relation litt�rale entre les flux thermiques impliqu�s pour le syst�me lorsque la montgolfi�re est � l’�quilibre thermique.

 Une partie du transfert thermique a lieu sous forme de rayonnement de l’enveloppe vers le milieu ext�rieur.
Le calcul du flux thermique rayonn� se fait gr�ce � la relation de Stefan-Boltzmann : Pr = e� s�S�T4
e le coefficient d’�missivit� constant sans unit�, pour l’enveloppe du ballon : e= 0,87 ;
s la constante de Stefan :  5,67 � 10–8 W�m–2�K–4;
S la surface de l’enveloppe ;
T la temp�rature de surface de l’enveloppe en K.
De plus, les mouvements de l’air ext�rieur le long de l’enveloppe sont � l’origine d’un flux thermique transf�r� vers l’ext�rieur par un ph�nom�ne de conducto-convection que l’on peut calculer gr�ce � la relation suivante : J = DT / Rth
J repr�sente le flux thermique perdu par le syst�me par conducto-convection en W ;
DT repr�sente la diff�rence de temp�rature entre l’enveloppe et le milieu ext�rieur en K ;
Rth repr�sente la r�sistance thermique associ�e au flux thermique entre l’enveloppe et le milieu ext�rieur : Rth = 3,5�10–4 K�W–1.
Pcomb +Pray re�ue+Pr + J + Pouverture=0.
Pcomb + e� s�S�T4 + Pr +DT / Rth + Pouverture=0.

D’apr�s l’�tude, dans ces conditions, la temp�rature de l’enveloppe vaut T = 325 K, temp�rature interm�diaire entre celle de l’air � l’int�rieur du ballon et celle de l’air � l’ext�rieur du ballon.
2.3. Calculer le flux thermique par rayonnement Pr �mis par l’enveloppe vers le milieu ext�rieur.
Pr = - e� s�S�T4 = 0,87 x 5,67 10-8 x 847 x 3254= -4,66 105 ~ -4,7 105 W.
 2.4. Calculer le flux conducto-convectif.
J = DT / Rth =(278-325) / (3,5 10-4) = -1,34 105 ~ -1,3 105 W.
 2.5. En d�duire que la valeur du flux thermique Pcomb associ� � la combustion du propane en r�gime de croisi�re est de l’ordre de 4�105 W.
Pcomb +Pray re�ue+Pr + J + Pouverture=0.
Pcomb = -Pray re�ue -Pr - J - Pouverture.
Pcomb = -1,9 105 +4,7 105 +1,3 105 +1,8 104 =4,3 105 W.
 Le flux thermique associ� � la combustion du propane n’est pas lib�r� de fa�on continue. En effet, la combustion du propane n’a lieu que lorsque le br�leur fonctionne. L’�nergie de combustion massique du propane est : Ecomb = 46,4 MJ�kg–1.
Le pilote actionne le br�leur pendant une dur�e t selon le fonctionnement d�crit sur la figure suivante. Lorsque le br�leur est en fonctionnement, 68 grammes de propane sont br�l�s chaque seconde.

 2.6. Montrer que le flux thermique associ� � la combustion du propane lorsque le br�leur est en fonctionnement est de l’ordre de 3�106 W.
t =2 s.
Masse de propane brul�e : m = 68 x2 = 136 g = 0,136 kg.
Pcomb = m Ecomb / t =0,136 x 46,4 / 2 ~3,2 MW = 3,2 106 W.
2.7. Dans les conditions de l’�tude, d�terminer la dur�e maximale de vol qu’il est possible de r�aliser � l’aide du propane embarqu� dans la montgolfi�re. Commenter.
0,136 kg de propane sont br�l�s � chaque Tbr�leur.
Masse de propane : 80 kg.
80 / 0,136 ~588.
Dur�e du vol : 588 x Tbr�leur = 588 x  20 =11 764 s ou 3 h16 min
Cette dur�e permet de survoler une r�gion assez vaste.

  
menu