Le spa gonflable
Un
spa gonflable permet de profiter d’une eau chauffée pour se détendre.
L’eau du spa est chauffée par une résistance électrique. Le spa est en
outre équipé d’un système permettant d’envoyer de l’air dans le fond du
spa pour faire
des bulles et d’un couvercle permettant de le fermer.
Le but de l’exercice est d’étudier les conditions de fonctionnement du
spa.
Données pour la situation étudiée :
− volume d’eau dans le spa rempli : V
eau = 795 L ;
− masse volumique de l’eau :
reau
= 1,00×10
3 kg m
-3;
− puissance de chauffage du spa : P
chauffage = 2,20×10
3
W ;
− capacité thermique massique de l’eau : c
eau = 4,18×10
3
J⋅K
-1⋅kg
-1.
Dans un premier temps, on s’intéresse à la mise en service du spa. Le
spa est rempli avec de l’eau à la température initiale T
i =
17 °C, puis le chauffage est mis en route. On suppose que la masse
d’eau dans le spa reste constante.
Q1. Exprimer la
capacité thermique C de l’eau du spa en fonction de V
eau,
reau et c
eau.
En déduire
l’expression puis la valeur de la variation d’énergie interne DU de l’eau du spa lorsque
sa température varie de Ti à la température Tf =
37 °C.
C = Veau reau
ceau=0,795 x1,0 103 x4,18 103=3,32 106
J K-1.
DU=C(Tf-Ti)
=3,32 106 (37-17)=6,65 107 J.
Q2. Montrer que la
valeur de la puissance thermique moyenne P reçue par l’eau du spa lors
de la mise en service est de l’ordre de 1,5 kW.
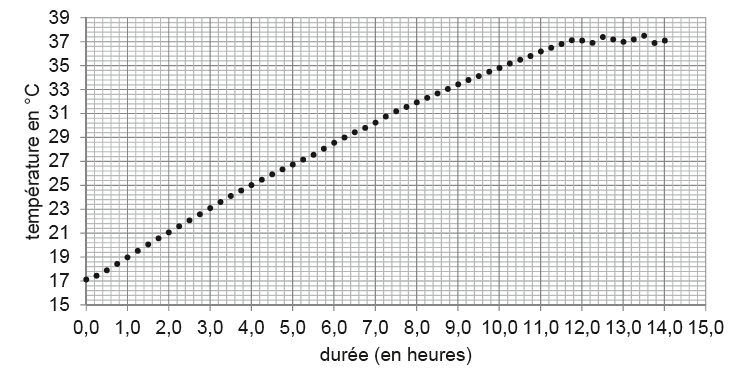
P =
DU / durée =6,65 107
/ (12 x3600) ~1,54 103 W ~1,5 kW.
Q3. Comparer cette
puissance thermique moyenne P reçue par l’eau du spa avec la puissance
de chauffage du spa Pchauffage et commenter.
P / P
chauffage = 1,5 / 2,2 ~0,68.
68 % de la puissance électrique sert à chauffer l'eau.
Dans cette partie, on s’intéresse aux pertes d’énergie thermique du spa
lorsque le système de chauffage est éteint.
La paroi du spa est constituée de deux couches de PVC de 4 mm
d’épaisseur, séparées par une couche d’air de 24 cm d’épaisseur. On
considère une température extérieure moyenne de 9 °C et une température
de l’eau moyenne de 37 °C.
Q4. Expliquer
qualitativement pourquoi il est, a priori, intéressant, d’un point de
vue thermique, que les parois soient remplies d’air.
L'air est un très bon isolant thermique.
Q5. Déterminer le
sens du transfert thermique dans cette situation. Justifier.
Le transfert thermique s'effectue de l'eau chaude vers l'extérieur, le
corps froid.
On considère le spa ouvert, le système de chauffage étant éteint. À
l’instant t = 0, la température vaut 37 °C.
On modélise le transfert thermique Q entre l’eau du spa et l’air
extérieur entre les instants t et t +
Dt par la loi de Newton :
Q = h . S . (T
ext - T(t)) .
Dt
Avec h le coefficient conducto-convectif surfacique, S l’aire de la
surface de l’eau en contact avec l’air, T
ext la température
de l’air extérieur, T(t) la température de l’eau du spa et
Dt
la durée d’étude supposée petite devant la durée typique d’évolution de
la température du système.
Q6. Établir
l’équation différentielle qui caractérise alors l’évolution temporelle
du système {eau du spa} et la mettre sous la forme :
dT / dt +T(t) /
t
= T
ext /
t.
avec t le temps caractéristique de l’évolution de la
température du système dont on donnera l’expression en fonction de h,
S, ceau, reau et Veau.
DU=Q ; Veau
reau
ceau dT(t) =h . S . (Text - T(t)) .dt.
dT(t) / dt = h . S . (Text - T(t)) /
( Veau reau
ceau).
On pose t = Veau
reau
ceau / (h S).
dT(t) / dt +T(t) / t
= Text / t.
L’évolution de la température peut être modélisée par une équation du
type :
T(t) = A . exp (-t /
t)
+B
Déterminer graphiquement la où A et B sont deux constantes que l’on ne
cherchera pas à déterminer. Une simulation de cette évolution est
proposée.valeur de
t.
Commenter.
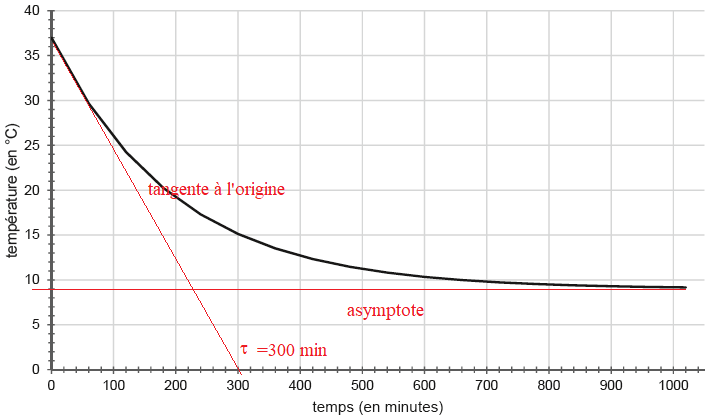
L'eau du spa se refroidit très lentement du fait de l'solation.
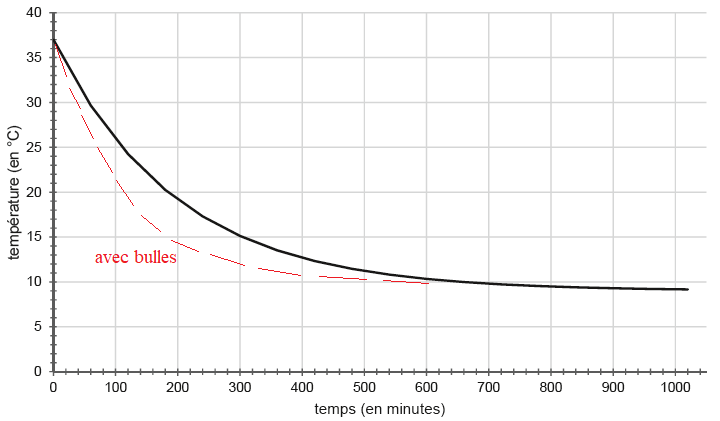
Dans les mêmes conditions que précédemment, on active les bulles du spa.
Q8. Expliquer
qualitativement comment évolue la valeur de
t comparée à la situation
précédente.
L'eau va se refroidir plus rapidement ;
t diminue.
Q9. Tracer alors
l’allure de la courbe d’évolution de la température que l’on
obtiendrait dans ce dernier cas.