Etude d'une frappe au football (10 points)
Dans un match de football, lors de phases de jeu
appelées dégagement, le gardien peut frapper le ballon de manière
contrôlée à condition de demeurer dans la surface de réparation. Il
s’agit d’envoyer le ballon haut et loin, de manière à pénétrer le camp
adverse.
Pour l’image 1, l’intervalle de temps est de 40 ms. Pour l’image 2,
l’intervalle de temps est de 33 ms et fait intervenir 106 photographies
entre la frappe et le rebond.
Effets d’un fluide sur le
mouvement d’une sphère dans un champ de pesanteur.
Une sphère en mouvement dans un fluide est ralentie du fait des
frottements. Lorsqu’elle est animée d’une rotation sur elle-même, la
sphère peut aussi faire l’objet d’un phénomène de portance. En plus
d’être ralentie, elle est alors aussi partiellement « portée » par
l’air.
Données :
− accélération de pesanteur : g = 9,81 m.s
-2.
Le ballon est immobile au sol avant la frappe. Dans un premier temps on
se place dans le cadre du modèle de la chute libre.
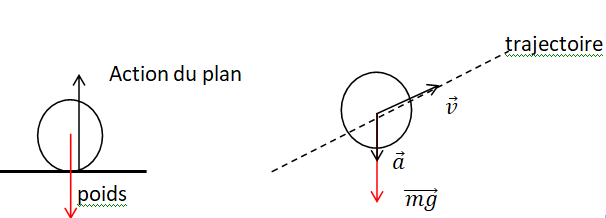
Q1. Effectuer un
bilan des forces exercées sur le système {ballon} avant et après la
frappe, en réalisant deux schémas sur lesquels figurent les vecteurs
force, vitesse et accélération.
Q2. Déterminer, à
l’aide de l’image 1, la valeur de la norme de la vitesse initiale.
Commenter.
Distance parcourue en 2x40 = 80 ms =0,08 s environ (1
2 +2
2)
½
~2,2 m .
Vitesse initiale = 2,2 / 0,08 ~28 m /s ou 28 x3,6 ~100 km /h, valeur
assez importante..
Q3. Pour les
expressions des composantes v
x et v
y fournies,
interpréter qualitativement leur signe au cours du temps.
v
x = v
0 cos
a t ;
vy = v0
sin a t -gt.
Jusqu'au sommet de la trajectoire : vx et vy
possèdent le sens des deux axes ; elles sont donc positives.
Au sommet vy = 0.
Au delà du sommet : vx >0 et vy <0.
Q4. Toujours
dans le cadre du modèle de la chute libre, déterminer la valeur de la
durée écoulée entre la frappe et l’impact au sol.
y = -½gt
2 + v
0 sin
a t = 0 au sol ; t ( ½gt +v
0sin
a) =0.
t = 0 ; frappe initiale ; t = 2 v
0 sin
a / g =2 x 28 x sin 22 / 9,8 ~2,1 s.
Q5. Toujours dans le
cadre du modèle de la chute libre, on suppose que la frappe est
effectuée par le gardien dans la surface de réparation avec le même
angle
a et la
même vitesse initiale v
0 . Déterminer par un raisonnement
quantitatif si le gardien est susceptible de marquer directement un but
sans rebond.
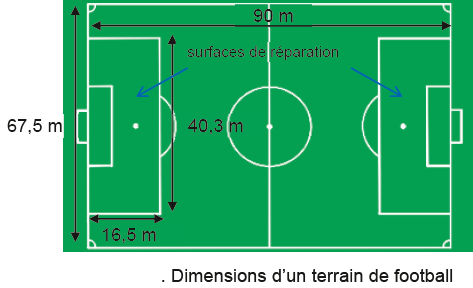
Non, car 57 < 90-16,5.
Q6. Au regard de la
chronophotographie de l’ensemble de la trajectoire (image 2), discuter
de la pertinence du modèle choisi compte tenu de la distance du point
d’impact d’une part et de la durée du vol du ballon entre l’instant de
la frappe et celui de l’impact.
L’intervalle
de temps est de 33 ms et fait intervenir 106 photographies entre la
frappe et le rebond.
Durée de la trajectoire : 106 x 0,033 ~3,5 s valeur 1,6
fois supérieure à la durée du modèle de la chute libre.
Le modèle de la chute libre ne convient pas.
La chronophotographie de l’image 1 met en évidence un mouvement de
rotation du ballon sur lui-même estimé à 5 tours par seconde.
Q7. Proposer une
interprétation à la valeur de la durée du temps de vol mesurée.
En 3,5 s, le ballon effectue 3,5 x5 ~ 18 tours sur lui même.
Le ballon est donc ralenti et subit un phénomène de portance par l'air.