Mesure de la taille des mailles d’un masque
respiratoire (10 points)
La conception des masques respiratoires dépend de
leur finalité, médicale, industrielle ou autre. Une des
caractéristiques importantes est la dimension des particules qu’ils
peuvent filtrer. Les virus peuvent être transportés par les
microgoutellettes expulsées lors de la respiration ou de l’éternuement.
Une toux génère des microgouttelettes de diamètre de
plusieurs dizaines de micromètres à une centaine de micromètres.
D’après https://www.esanum.fr
La filtration obtenue grâce aux masques repose-t-elle uniquement sur un
effet de « passoire » ?
Donnée :
− expression de l’interfrange i d’une figure d’interférences pour une
lumière monochromatique de longueur d’onde
l traversant un système de
fils parallèles séparés d’une distance b , l’écran étant éloigné d’une
distance D du système de fils :
i =
l × D / b.
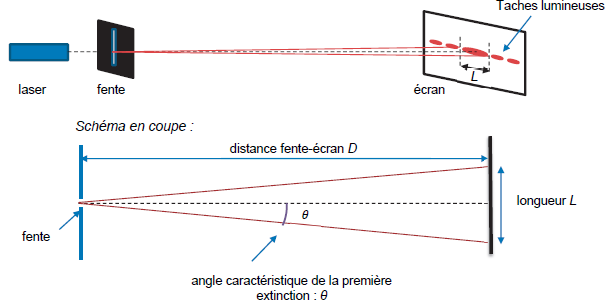
Lors de l’expérience n°1, une fente de largeur a = 0,15 mm est éclairée
par un rayonnement issu d’un laser. L’expérimentateur mesure la
longueur L de part et d’autre de la tâche centrale obtenue sur un écran
pour une distance fente-écran, notée D, variable. Il déduit de ces
mesures la valeur de la longueur d’onde
l de la lumière émise par le
laser.
D(m)
|
1,000
|
1,500
|
1,800
|
2,300
|
2,800
|
L(cm)
|
0,82
|
1,37
|
1,49
|
2,09
|
2,48
|
l(nm)
|
615
|
685
|
621
|
682
|
664
|
Q1. Nommer le
phénomène ondulatoire exploité par cette expérience.
Diffraction par une fente.
Q2. Déterminer la
valeur de la moyenne de la longueur d’onde
l.
(615 +685 +621 +682 +664) / 5 ~653 nm.
. On admet que l’incertitude-type, u(
l), associée à la
détermination de la longueur d’onde par cette
expérience vaut 13 nm.
Q3. Comparer le
résultat obtenu avec la valeur de référence donnée par le fabricant du
laser qui indique une longueur d’onde de valeur λ = 650 nm.
La longueur d'onde appartient à l'intervalle [640 ; 666 nm]. La valeur
de référence appartient à cet intervalle.
Une nouvelle expérience est réalisée à partir de la première expérience
: la fente simple est remplacée par une double fente ; le reste du
dispositif étant inchangé, et l’écran est placé àla distance D = 2,23
m. C’est l’expérience n°2.
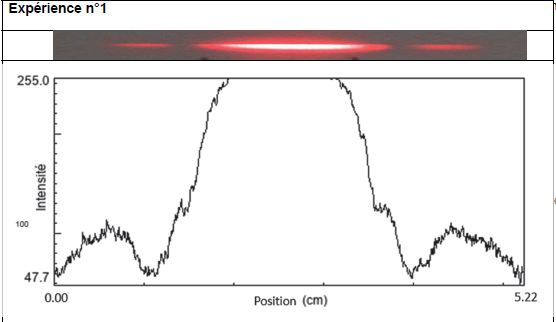
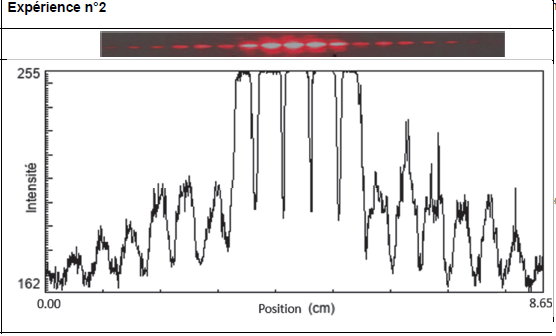
Un logiciel de traitement d’image permet d’obtenir la distribution de
l’intensité lumineuse le long de la tâche obtenue sur l’écran. Les
résultats obtenus pour les deux expériences sont présentés ci-après.
 Q4
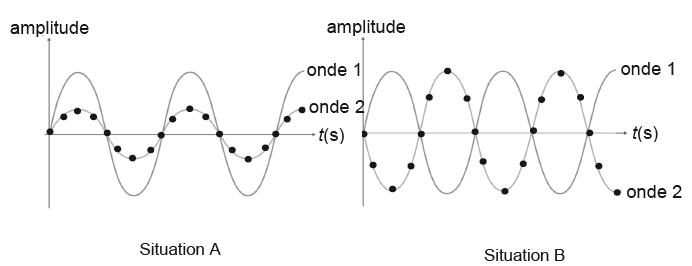
Q4. Nommer les
phénomènes physiques sous-jacents à l’expérience n°2.
Chaque fente provoque un phénomène de diffraction.
La fente double conduit à un phénomène d'interférences.
Un masque respiratoire en tissu est réalisé en superposant deux couches
de tissu. Chaque couche de tissu est constituée d’une trame de fils
horizontaux et de fils verticaux. La double fente de l’expérience n°2
est remplacée par une couche de tissu modérément tendu, les autres
conditions de l’expérience (nature du laser, distance fente-écran D =
2,23 m) restant
inchangées.
 Q5.
Q5. En utilisant
les données, estimer la valeur de la distance séparant deux fils
horizontaux.
2,1 cm ~ 4 interfranges ; i = 2,1 / 4 =0,525 cm = 5,25 10
-3
m.
i =l × D / b.
b = l × D / i =650 10-9
x2,23 /(5,25 10-3) ~2,76 10-4 m=276 µm.
Q6. Comparer la
taille d’une maille (maille = trou) d’un masque, avec les dimensions
des microgouttelettes expulsées lors de la respiration ou de
l’éternuement. On néglige ici l’épaisseur des fils.
Une toux génère des microgouttelettes de
diamètre de plusieurs dizaines de
micromètres à une centaine de micromètres.
La taille d’une maille (maille = trou) d’un masque est
bien supérieure à celle des microgoutellettes.
Les masques homologués ont une efficacité de filtration des
microgouttelettes très proche de 100 %.
Q7. Commenter ce
résultat au regard de votre réponse à la question précédente.
La filtration
obtenue grâce aux masques ne repose pas uniquement sur un effet de «
passoire ».
Les particules se collent durablement aux fils grâce à des interactions
électriques de faible intensité ( force de Van der Waals).