Mathématiques, QCM : suite, fonctions, Bac Métropole 9 /9 / 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Sujet 1. 7 points. Une seule des 4 réponses proposées est exacte.   1. On considère la fonction g définie sur R par : g(x) = 2ex /(ex+1). La courbe représentative de g admet pour asymptote en +oo la droite d'équation : a. x =2 ; b. y = 2 vrai ; c. y = 0 ; d. x = -1. g(x) = 2 / (1+e-x). Quand x tend vers +oo, e-x tend vers zéro et g(x) tend vers 2. La droite d'équation y = 2 est asymptote.   2. On considère une fonction f définie et 2 fois dérivable sur R. On appelle C sa représentation graphique. On désigne par f " sa dérivée seconde. On a représenté la courbe de f " notée C". 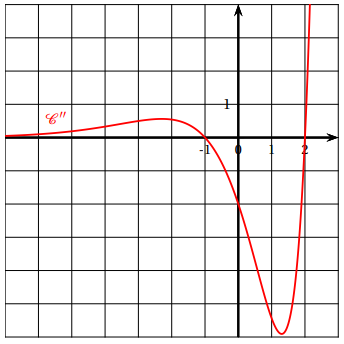a. C admet un unique point d'inflexion. b. f est convexe sur [-1 ; 2]. c. f est convexe sur ]-oo ; -1] et sur [2 ; +oo[. Vrai. d. f est convexe sur R. La dérivée seconde s'anulle est change de signe en x = -1 et en x = 2 : donc deux points d'inflexion. f " est positive sur ]-oo ; -1] et sur [2 ; +oo[ ; f est donc convexe sur ces intyervalles. 3. On donne la suite (un) définie par u0 = 0 et pour tout entier naturel n , un+1 = 0,5 un+1. La suite (vn) définie pour tout entier naturel n par vn = un-2 est : a. arithmétique de raison -2. b. géométrique de raison -2. c. arithmétique de raison 1. d. géométrique de raison 0,5. Vrai. vn+1 = un+1 -2 =0,5 un -1 =0,5(un-2) = 0,5 vn. 4. On considère la suite (un) telle que, pour tout entier naturel , on a : 1 + 0,25n < un < 2-n /(n+1). On peut affirmer que la suite (un) : a. converge vers 2. b. converge vers 1. Vrai. c. diverge vers  plus l'infini. d. n'a pas de limite. Quand n tend vers plus l'infini : 0,25n tend vers 0 et n / (n+1) = 1 /(1 +1/n) tend vers zéro. Par suite 1 < limite de un en +oo < 1. 5. Soit f la fonction définie sur ]0 ; +oo[ par f(x) = x2 ln(x). Une primitive F de f sur cet intervalle est définie par : a. F(x) = x3 / 3 (ln(x-1/3). Vrai. On dérive en posant u = x3 / 3 ; v = ln(x-1 /3) ; u' = x2 ; v' = 1 / x. u'v+v'u = x2 ln(x-1 /3) +x3 / (3x)= x2 ln(x)-x2 /3) +x2 /3= x2 ln(x) = f(x) b. F(x) = x3/3 (ln(x-1). c. F(x) = x2 . d. F(x) = x2 / 3 (ln(x-1) 6. Pour tout réel x, l'expression A = 2+(3e-x-5) / (e-x+1) est égale à : a. (5-3ex) /(1+ex). Vrai. b. (5+3ex) /(1-ex). c. (5+3ex) /(1+ex). d. (5-3ex) /(1-ex). Réduire au même dénominateur puis multiplier numérateur et dénominateur par ex. A = [2 e-x+2 +3e-x-5 ] / (e-x+1)=(5e-x-3 ] / (e-x+1)=(5-3ex) / (1+ex). ... .... Sujet 2. 7 points.   On considère les suites (an) et (bn) définie par a0 = 1 et, pour tout entier naturel n, an+1 = 0,5an +1 et bn = an −2. On peut affirmer que :  a. (an) est arithmétique;  b. (bn) est géométrique;  vrai c. (an) est géométrique;  d. (bn) est arithmétique. bn+1 =an+1-2 = 0,5 an+1-2 =0,5 an -1 =0,5(an-2) = 0,5 bn.  Dans les questions 2. et 3., on considère les suites (un) et (vn) définies par : u0 = 2, v0 = 1 et, pour tout entier naturel n : un+1 = un +3vn ;  vn+1 = un + vn. 2. On peut affirmer que : a.  u2 = 5 ; v2 = 3  b. u 2 2 −3v 2 2 = −2 2 c. u2 / v2 = 1,75 vrai d. 5u1 = 3v1. u1 = u0 +3v0=2+3=5. v1 = u0 + v0= 3. u2 = u1 +3v1=5+9=14. v2 = u1 + v1= 8. u2 / v2 =14 / 8 = 7 / 4 = 1,75. 3. On considère le programme ci-dessous écrit en langage Python : def valeurs() : u = 2  v = 1 for k in range(1,11) c = u u = u + 3*v v = c + v return (u, v). Ce programme renvoie :  a. u11 et v11 vrai ; b. u10 et v11 ; c. les valeurs de un et vn pour n allant de 1 à 10;  d. u0 et v10. Pour les questions 4. et 5., on considère une fonction f deux fois dérivable sur l’intervalle [−4 ; 2]. On note f ′ la fonction dérivée de f et f ′′ la dérivée seconde de f . On donne ci-dessous la courbe représentative C ′ de la fonction dérivée f ′ dans un repère du plan.  On donne de plus les points A(−2 ; 0), B(1; 0) et C(0; 5). 4. La fonction f est : a. concave sur [−2 ; 1];  b. convexe sur [−4 ; 0]; vrai c. convexe sur [−2 ; 1];  d. convexe sur [0; 2]. f ' est croissante sur [-4 ; 0]; f " est positive  et f est convexe sur cet intervalle.  5. On admet que la droite (BC) est la tangente à la courbe C ′ au point B. On a : a. f ′ (1) < 0 ; b. f ′ (1) = 5 ; c. f ′′(1) > 0 ; d. f ′′(1) = −5. Vrai. Le coefficient directeur de la droite (BC) est f "(1)= -5. 6. Soit f la fonction définie sur R par f (x) = ( x 2 +1 ) e x . La primitive F de f sur R telle que F(0) = 1 est définie par : a. F(x) = ( x 2 −2x +3 ) e x ; ne convient pas car F(0) = 3  b.  ( x 2 −2x +3 ) e x −2; vrai On calcule F'(x) en posant u = x 2 −2x +3 et v =e x. u' = 2x-2 ; v' = ex. u'v+v'u = 2(x-1)ex+ex( x 2 −2x +3 ) =ex(x2+1)= f(x).  c. F(x) = ( 1 /3 x 3 + x ) e x +1; d. F(x) =( 1/ 3 x 3 + x ) e x ne convient pas car F(0) = 0.

menu