La physique du jonglage, bac Métropole 2022. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . .. .. ...... ... Dans cette étude : - on note (x ; y) les coordonnées de la position de C dans le repère (O ; x ; y) et (vx ; vy) celles de sa vitesse ; - les évolutions temporelles y(t) et vy(t) sont respectivement représentées qui font apparaître alternativement des phases notées 1 et 2 - à la date t = 0 s la balle, située à l’origine du repère, quitte pour la première fois la main du jongleur avec une vitesse initiale v0 ;  - lorsque la balle n’est pas en contact avec la main du jongleur, elle est en chute libre. Elle effectue alors un mouvement parabolique en passant d’une main à l’autre, la réception et le lancer se faisant toujours en y = 0 m ; - la référence de l’énergie potentielle de pesanteur est choisie à l’ordonnée y = 0 m. 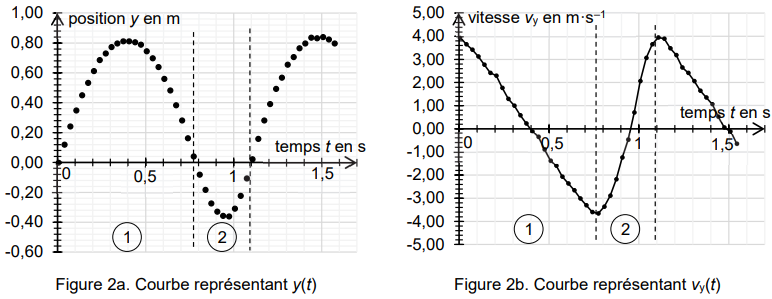Q1. Décrire qualitativement, selon l’axe Oy, le mouvement de la balle lors de la phase 1 à l’aide des figures 2a et 2b. La vitesse vy(t) varie linéairement ; elle est positive pendant la montée, s'annule au maximum, puis est négative ( lors de la descente); l'altitude y(t) croît, passe par un maximum, puis décroît  ( mouvement parabolique). Q2. Interpréter la figure 2a pour décrire le rôle de la main sur le mouvement de la balle lors de la phase 2. La main en amortissant la balle descend puis elle donne une impulsion à la balle afin qu'elle puisse remonter et quitter la main. Q3. Justifier à l’aide de la deuxième loi de Newton, dans le cadre du modèle de la chute libre, que la valeur de la composante vx de la vitesse est constante et égale à la vitesse initiale v0x lorsque la balle n’est plus en contact avec la main du jongleur. La balle est en chute libre ( soumise uniquement à son poids). La seconde loi de Newton conduit à : ax = 0 ; ay = -g. La vitesse est une primitive de l'accélération. vx = cste = v0x ; vy = -gt +cste = -gt +v0y.  Q4. Exprimer l’énergie mécanique initiale Em0 de la balle en fonction de sa masse m et des composantes v0x et v0y de la vitesse initiale dans le référentiel terrestre. L'énergie potentielle initiale étant nulle, l'énergie mécanique est sous forme cinétique. Em0 = ½mv2 = ½m(v0x2 +v0y2).  Dans toute la suite de l’exercice, on ne s’intéresse qu’à la phase 1. Q5. À l’aide d’un raisonnement énergétique appliqué lors de la phase 1, établir que l’expression de l’altitude maximale H atteinte par la balle s’écrit : H = v0y 2 / (2g) . A l'altitude maximale, la composante verticale de la vitesse est nulle. L'énergie mécanique est : E = mgH + ½m v0x2 . Conservation de l'énergie mécanique : ½m(v0x2 +v0y2) = mgH + ½m v0x2 . ½mv0y2 = mgH. ½v0y2 = gH ; H = v0y 2 / (2g) . Q6. Déterminer la valeur de H à partir de la relation précédente et d’une lecture graphique de v0y sur la figure 2b. Comparer le résultat à celui obtenu par lecture graphique de la figure 2a. voy = 4 m /s. H = 16 / (2 x9,81) ~0,82 m. En accord avec la valeur ( 0,80 m) lue sur la figure 2a. Q7. Établir l’expression littérale de la coordonnée vy(t) du vecteur vitesse de la balle lors de la phase 1. La vitesse est une primitive de l'accélération : vy(t) = -gt +v0y. Q8. Évaluer l’intensité de la pesanteur g à l’aide de la figure 2b lors de la phase 1. Commenter. A t = 0,4 s, vy =0. 0=-4g +4 ; g = 10 m s-2, en accord avec la valeur 9,81 m s-2. ( écart relatif 2 %).  Q9. Déterminer l’équation horaire y(t) du mouvement du centre de la balle lors de la phase 1 La position est une primitive de la vitesse et la position initiale est l'origine de l'axe. y(t) = -½gt2 +voyt. Q10. On note tair la durée pendant laquelle la balle est en l’air lors de la phase 1. Établir l’expression de tair en fonction de v0y et de g. En déduire que l’expression du temps de vol dans l’air d’une balle s’écrit : tair = (8H / g)½. 0 = -½gtair2 +voytair. Première solution tair =0 ( position initiale). Seconde solution : -½gtair +voy =0 ; tair = 2voy / g. Or H = v0y 2 / (2g) . voy = (2gH)½. tair = 2(2gH)½ / g =(8H / g)½. Q11. Calculer la valeur de tair en utilisant la valeur de H obtenue par lecture graphique de la figure 2a. Commenter. H =0,80 m ; tair = (8 x 0,8 / 9,81)½~0,8 s.( en accord avec la valeur lue sur la graphe 2a ). Les frottements de l'air ne sont pas négligeables.

menu