Un fil
de suture en chirurgie permet de rapprocher les deux bords d’une
plaie afin de faciliter la cicatrisation. Le diamètre, la forme et la
composition
chimique des fils sont adaptés au type de tissu à recoudre (peau,
muscle,
tendon, nerf, etc.) mais aussi à la durée de cicatrisation et à la
taille de la
plaie.
Lors de la fabrication d’un fil, les industriels peuvent notamment
contrôler
son diamètre à l’aide d’appareils utilisant la diffraction de la
lumière d’un
laser.
Dans cet exercice, on étudie le principe physique utilisé dans un
appareil de contrôle du diamètre d’un fil puis
on s’intéresse à un fil de suture vendu en pharmacie.
Données : longueur d’onde du laser utilisé :
l = 532 nm ;
1. Principe physique utilisé par un appareil de contrôle du diamètre d’un fil.
Pour illustrer ce principe au laboratoire, on place, sur un banc d’optique, un laser émettant une onde de
longueur d’onde
l et un fil de diamètre a connu. Un écran est placé à une distance D du fil. La largeur L de la
tache centrale de la figure de diffraction est mesurée directement sur l’écran.
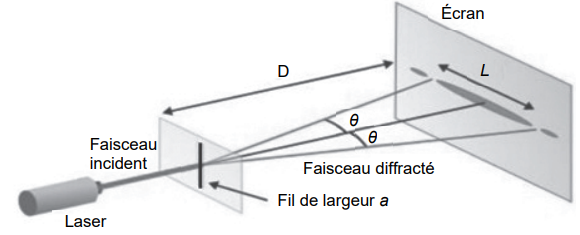 Q1.
Q1. Indiquer qualitativement comment évolue l’angle caractéristique de diffraction
q avec le diamètre a du fil.
q = l /a
avec a et l en mètres.
L’angle caractéristique de diffraction q et le diamètre a du fil.sont inversement proportionnels pour une longueur d'onde donnée.
q augmente si le diamètre du fil diminue.
Q2. Écrire la relation entre l’angle caractéristique de diffraction
q et les grandeurs D et L.
tan q
= ½L / D.
Pour les petits angles : q
~ ½L
/ D avec q
en radian.
Q3. Établir l’expression de la largeur L de la tache centrale de la figure de diffraction en fonction de
l, D et a.
q
~ ½L
/ D et q = l /a.
L = 2 l D / a.
On réalise la mesure de la largeur de la tache centrale de la figure de diffraction pour sept fils de diamètres a
connus. On représente alors L en fonction de 1/a.
Q4. Vérifier que les résultats expérimentaux sont cohérents avec l’expression établie à la
question Q3.
Q5. Montrer que la modélisation suivante permet de rendre compte des résultats expérimentaux :
L = 1,6×10
−6 ×
1
/a
avec a et L exprimés en m.
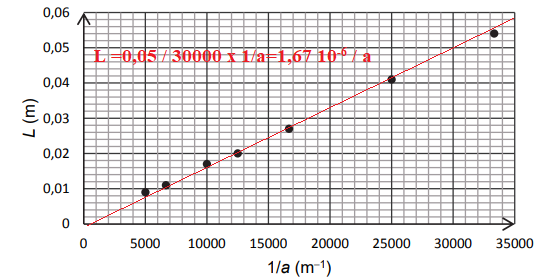
Les points sont alignés sur une droite passant par l'origine. L est proportionnelle à 1 /a.
Coefficient directeur de la droite : 0,05 / 30000 =1,67 10
-6.