Vitesse de la station spatiale internationale, Bac Métropole 9 /9 / 2022. Lunette astronomique. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... La Station Spatiale Internationale (ISS) est un satellite artificiel de la Terre, observable de la surface de la Terre sous certaines conditions. C’est ainsi que, le 24 juin 2020, dans l’état de Virginie aux États-Unis, un astrophysicien a observé et enregistré le passage de l’ISS devant le Soleil. Pendant ce passage, la station spatiale se trouve entre le Soleil et le point d’observation. En réalisant une chronophotographie, on obtient l’image reproduite sur la figuresuivante.  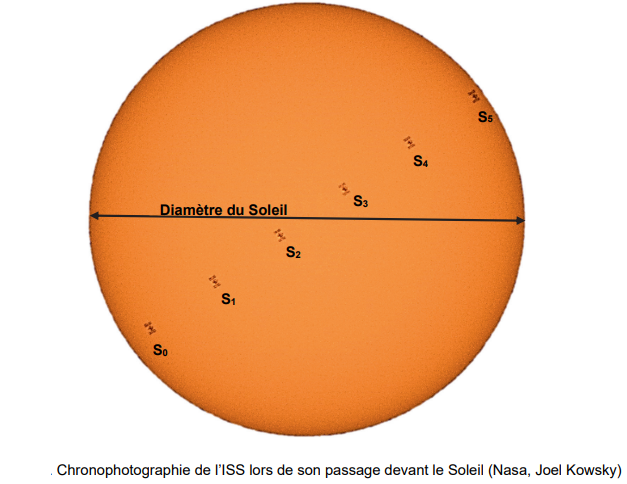Le but de cet exercice est de déterminer la vitesse de l’ISS à l’aide d’une loi de la mécanique puis en exploitant la chronophotographie et de comparer les résultats obtenus. Données :  altitude moyenne de l’ISS : h = 419 km ;  constante de gravitation universelle : G = 6,67×10–11 m3·kg–1·s–2 ;  distance Terre-Soleil : dTS = 153×106 km ;  diamètre du Soleil : D = 1,39×106 km ;  masse de la Terre : M = 5,97×1024 kg ;  rayon de la Terre : RT = 6 371 km. 1. Détermination de la vitesse à l’aide d’une loi de la mécanique.  La Station Spatiale Internationale est modélisée par un point matériel M, de masse m en orbite circulaire à la distance r du centre de la Terre. La Terre est supposée à répartition sphérique de masse, de centre T. Le mouvement de l’ISS est étudié dans le référentiel géocentrique d’origine prise au centre de la Terre et dont les axes pointent en direction d’étoiles lointaines ; il est supposé galiléen. On considère que seule l’interaction gravitationnelle avec la Terre est prise en compte. Q1. Schématiser, sans souci d’échelle, la Terre et l’ISS. Placer le repère de Frenet  et représenter la force à laquelle est soumise l’ISS.  Q2. Donner, dans ce repère, l’expression vectorielle de la force à laquelle est soumise l’ISS.  Q3. 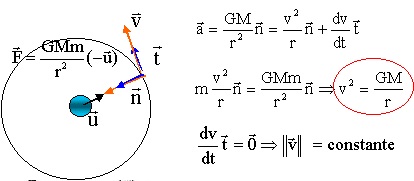Déduire de la seconde loi de Newton, l’expression suivante de la vitesse v de l’ISS : Q4. Calculer la valeur de la vitesse v de l’ISS. r = RT+h =(6371 +471)103=6,84 103 km = 6,84 106 m. v = [6,67 10-11 x 5,97×1024/ (6,84 106)]½ =7,6 103 m /s. ... .... 2. Estimation de la vitesse de l’ISS à partir d’une chronophotographie.  Le télescope utilisé pour réaliser la chronophotographie lors du passage de l’ISS devant le Soleil est situé au point O. Les positions réelles successives de la station sont repérées par des points Mi, i allant de 0 à 5. Les points Si, i allant de 0 à 5, correspondent à la projection des points Mi sur le disque solaire, vus de la Terre . La distance S0S5 observée permet de déterminer la distance parcourue par l’ISS notée M0M5. La figure représente, sans souci d’échelle, la situation. Les points M0 et M5 correspondent aux positions extrêmes de l’ISS pendant l’observation, ainsi que leur projection sur le disque solaire S0 et S5. La durée du mouvement entre deux positions successives (exemple de M0 à M1, de M1 à M2…) vaut Dt = 0,11 s. Dans cette partie, l’étude est réalisée dans le référentiel terrestre et les hypothèses formulées sont les suivantes : - le mouvement de la station est rectiligne uniforme pendant la durée nécessaire à la réalisation de la chronophotographie ;  - les effets des mouvements de rotation de la Terre sur elle-même et de révolution de la Terre autour du Soleil ne sont pas pris en compte ;  - M0M5 et S0S5 sont considérés comme étant des droites. Q5. En exploitant notamment la chronophotographie donnée, estimer la valeur de la vitesse v de l’ISS dans le référentiel d’étude lors de l’observation. Commenter la valeur obtenue au regard de celle calculée à la question  Q4. Donner au moins un argument qui justifie l’écart constaté. SOS5 ~0,932 D =0,932 x1,39 106 =1,3 106 km. M0M5 = SOS5 h / dTS =1,3 106 x 419 / (153 106) =3,55 km. Durée de ce parcours : 5 Dt = 0,55 s. Vitesse de l'ISS : 3,55 / 0,55 ~6,5 km / s. Ecart : (7,6-6,5) / 7,6 ~0,14. M0M5 et S0S5 ne doivent pas être considérés comme étant des droites.

menu