Observer les anneaux de Saturne, Bac Métropole 9 /9 / 2022. Lunette astronomique. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Les anneaux de Saturne sont parmi les objets les plus fascinants et les plus accessibles à l’observation pour l’astronome amateur. Selon la qualité de l’instrument d’observation, on peut distinguer plusieurs niveaux d’observation de cette planète. On présente  les 4 premiers niveaux accessibles à l’astronome amateur : Dans cet exercice, on s’intéresse à une lunette astronomique commerciale et on cherche à déterminer quel niveau d’observation de Saturne elle permet d’atteindre. Données :  dans tout l’exercice on admet l’approximation des petits angles suivante valable pour tout angle a, exprimé en radian, très petit par rapport à 1 rad : tan a ≈ a ;  la lunette astronomique étudiée possède un objectif de distance focale ݂f1 ′ = 700 mm et peut être associée à différents oculaires. 1. Modélisation optique de la lunette astronomique commerciale.  La lunette astronomique que l’on propose d’étudier est modélisée par deux lentilles minces convergentes, notées L1 et L2, possédant le même axe optique. La modélisation de cette lunette est proposée où sont indiqués le foyer objet F2 de la lentille L2 et les foyers images F’1 et F’2 des deux lentilles. Dans cette première partie, on s’intéresse aux trajets des rayons lumineux modélisant la propagation de la lumière dans la lunette. On note ݂f 2 ′ la distance focale de la lentille L2. Q1. Indiquer les noms « objectif » et « oculaire » de chaque lentille. L1 : objectif ; L2 : oculaire. Q2. Justifier que la lunette astronomique modélisée constitue un système optique afocal. La lunette est afocale car elle donne d'un objet située à l'infini, une image située à l'infini.  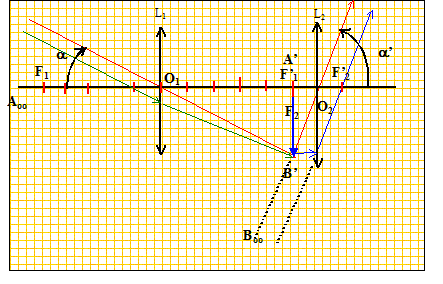Q3. Construire, sur la figure , l’image d’un objet à l’infini vu sous un angle a, formée par la lunette astronomique, en construisant l’image intermédiaire et en faisant apparaître l’angle a’, angle sous lequel est vue l’image finale en sortie de lunette. Q4. Donner la définition du grossissement G de la lunette astronomique en fonction des angles a et a’. G = a' / a. Q5. Établir l’expression suivante du grossissement de la lunette astronomique :  G = f 'obj / f 'ocu. tan a = A'B' / O1F'1 = A'B' / f 'obj proche de a radian si l'angle est petit. tan a' = A'B'  / f 'ocu proche de a' radian si l'angle est petit. G = a ' / a ; G = f 'obj / f 'ocu. Q6. En déduire la valeur de la distance focale ݂f2′ de l’oculaire à choisir afin d’obtenir une lunette astronomique dont le grossissement est de 78. 78 = f '1 / f '2 : f '2 =700 / 78 ~9 mm. ... .... 2. Observation des anneaux de Saturne.  On utilise la lunette astronomique de grossissement 78 modélisée dans la partie précédente pour observer Saturne et essayer de distinguer ses anneaux. Données :  distance moyenne entre les centres de la Terre et de Saturne : D = 1,4×109 km ;  distance entre la surface de Saturne et l’extrémité la plus proche de l’anneau C (anneau le plus proche considéré visible) : dmin = 1,4×104 km ;  distance entre la surface de Saturne et l’extrémité la plus éloignée de l’anneau A (anneau le plus éloigné considéré visible) : dmax = 7,7×104 km ;  largeur de la division de Cassini : dcas = 4,8×103 km ;  rayon de Saturne : RS = 5,8×104 km considéré comme faible devant D. angle minimal à partir duquel notre œil peut distinguer deux objets très proches : ε = 2,9×10-4 rad. Si q < e l’observateur ne peut pas distinguer l’objet 1 de l’objet 2. Q7. Décrire, en s’appuyant sur un calcul, comment apparaît Saturne à un observateur lors d’une observation à l’œil nu. q = 2 RS / D = 2 x5,8 104 / (1,4 109)=8,3 10-5 rad. Cette valeur étant inférieure à e, l'observateur ne distingue pas Saturne de ces anneaux ( anneaux non visibles). Q8. Déterminer le niveau d’observation de Saturne  que l’on atteint avec la lunette astronomique utilisée. G = 78 ; 2,9 10-4 / 78~3,7 10-6 rad. L'anneau A est t-il visible ? dmin / D =1,4 104 / (1,4 109) =10-5 rad > 3,7 10-6 rad. Cet anneau est  visible. L'anneau C est t-il visible ? dmax / D =7,7 104 / (1,4 109) =5,5 10-5 rad > 3,7 10-6 rad. Cet anneau est visible. La division de Cassini est-elle visible ? dcas / D =4,8 103 / (1,4 109) =3,4 10-6 rad < 3,7 10-6 rad. Cette division n' est pas visible. Donc niveau 3 d'observation.

menu