Le rover américain Persévérance, qui s'est posé sur la
planète Mars le 18 février 2021 dans le cratère Jezero,
est un véhicule de la taille d'une voiture et équipé de
multiples capteurs et instruments de mesure.
Après six mois et demi de voyage environ, le rover
américain, protégé dans sa capsule, a accompli un
enchaînement délicat et rigoureux d’actions pour se
poser. Tout s'est joué en seulement 7 minutes : « les
sept minutes de terreur ».
Cet enchainement délicat se déroule en 4 phases ;
comme présenté sur la figure 1 :
• phase 1 : la descente ralentie du Sky Crane portant
le rover
• phase 2 : le surplace du Sky Crane
• phase 3 : la descente à vitesse constante suivie du
dépôt du rover
• phase 4 : l'éjection du Sky Crane.
intensité du champ de pesanteur au voisinage de la surface de Mars : g = 3,7 m∙s
-2
Études cinématique et dynamique lors de la descente autopropulsée (phases 1 à 3)
Dans cette première question, le système étudié est l'ensemble « Sky Crane + rover
Persévérance » (assimilé à un point matériel) dans un référentiel considéré galiléen lié à
Mars. Pour simplifier l’étude, on considèrera que les mouvements étudiés sont rectilignes et
que les frottements sont négligeables.
1. Compléter le tableau. On notera F la
force de propulsion des rétrofusées du Sky Crane, qui permettent de ralentir ou
d’empêcher la descente de l'ensemble. Les vecteurs (forces, vitesse ou accélération)
seront représentés sans souci d’échelle. Leurs longueurs devront cependant être
cohérentes avec la situation étudiée ainsi qu’avec leurs évolutions au cours du temps.
Éjection du Sky Crane une fois le rover déposé (phase 3 à 4).
Mouvement étudié
|
Etude cinématique
(représenter la vitesse et l'accélération)
|
Etude dynamique
( représenter F)
|
Justifier l'étude dynamique à partir d'une loi.
|
La descente ralentie entre (1) et (2)
|
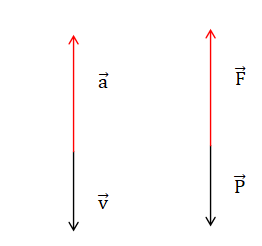
|
Seconde loi de Newton.
|
Le surplace (2).
|
Vitesse et accélération nulles.
F et P se compensent.
|
Première loi de Newton.
|
La descente à vitesse constante entre (2) et (3)
|
Accélération nulle ; vitesse constante.
F et P se compensent.
|
Première loi de Newton. |
Pour la suite de cette partie, le système étudié est limité au seul Sky Crane, assimilé à un
point matériel, noté M. Dès que le rover a été déposé, le Sky Crane monte à la verticale jusqu’à
une altitude H de 60,0 m au-dessus du sol martien, puis s'incline d’un angle
a = 45,0 ° par
rapport à l’horizontale et une force propulsive l'éjecte loin du lieu d'atterrissage du rover, avec
une vitesse initiale v
0 = 25,0 m∙s
-1. La force propulsive cesse à t = 0 s.
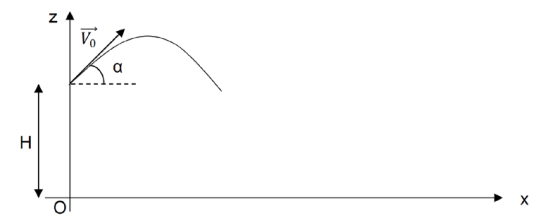 2.
2. À partir de t = 0 s, les forces de frottements sont négligées. Citer la seule force
s'appliquant sur le Sky Crane et qualifier ainsi la nature de la chute ainsi obtenue.
Le système n'est soumis qu'à son poids. Il s'agit d'un mouvement de chute libre avec vitesse initiale.
3. Établir l'expression des composantes de l’accélération, celles de la vitesse du Sky Crane
et enfin celle des coordonnées de sa position en fonction du temps.
a
x = 0 ; a
z = -g.
La vitesse est une primitive de l'accélération :
v
x = v
0 cos
a ; v
z = -gt +v
0 sin
a.
La position est une primitive de la vitesse.
x =
v0 cos a t ; z = -½gt2 +v0 sin a t + H.
4. Montrer que l’équation de la trajectoire du Sky Crane s’écrit : z(x) = − ½ g [x /( v
0cos
a)]
2 + tan
a x +H.
Préciser le type de trajectoire auquel correspond cette équation.
t = x / (
v0 cos a) ; repport dans z :
z = -½g[ x / (v0 cos a) ]2 +v0 sin a [x / (v0 cos a)] + H.
z(x) = − ½ g [x /( v0cos a)]2 + tan a x +H.
Il s'agit d'une trajectoire parabolique.
5. Pour des questions de sécurité évidente et afin de ne pas endommager le rover
Persévérance qui a été déposé sur le sol martien en O, le Sky Crane doit être éjecté au
minimum à 200 m de distance du lieu d'atterrissage du rover. Dans ces conditions
opératoires, vérifier que le Sky Crane atteint bien la distance de sécurité.
z(x) = − ½ g [x /( v0cos a)]2 + tan a x +H = 0.
-0,5 * 3,7 /(25 cos 45)2 x2+ x tan 45 +60 = 0
-5,92 10-3 x2 +x +60 = 0.
Discriminant D = 1+60 *4 *5,92 10-3 =2,42~1,562.
On retient la solution positive : x = (-1 -1,56) / (-2*5,92 10-3) =2,2 102 m.
La distance de sécurité est atteinte.
.