La
pâte à pizza, bac Liban 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
A. Gonflement de la pâte et production de dioxyde de carbone.
Les
évolutions temporelles des quantités d'éthanol, de glucose et de
dioxyde de carbone lors d'une fermentation à partir de 100 g de farine sont représentées.
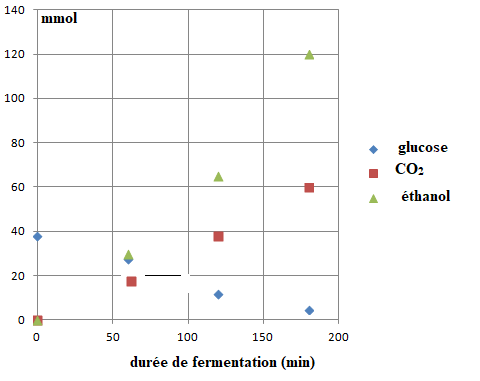
1. Vérifier qualitativement les évolutions temporelles.
Le glucose, le réactif : la quantité de matière diminue au cours du temps.
Etanol et CO2 les produits : leurs quantités de matière augmentent.
2. La hauteur de la pâte augmente au cours du temps. Quelle espèce chimique en est responsable ?
Le gaz, le dioxyde de carbone.
3. On
admet que la réaction s'effectue dans un milieu à volume constant V = 1
L. Déterminer la vitesse volumique moyenne d'apparition de l'éthanol
sur une durée de 3 heures. Même question pour la vitesse de disparition
du glucose.
Ethanol : 120 / 3 = .40 mmol h-1.
Glucose : 33 / 3 = 11 mmol h-1.
4. Effectuer le rapport de ces valeurs et indiquer si ce rapport est cohérent ou non avec la modélisation proposée.
C6H12O6(s) --> 2C2H5OH(l) + 2CO2(g)
Daprès les nombres stoechiométriques, la vitesse de disparition du
glucose devrait être égale à la moitié de la vitesse d'apparition des
produits. ( or on trouve un rapport proche de 4. )
5. La vitesse de disparition du glucose est-elle plus faible ou plus élevée que celle attendue ? Proposer une explication.
La vitesse de disparition du glucose est plus faible que celle attendue.
D'autres sucres présents dans la pâte ( saccharose, maltose) donnent du dioxyde de carbone.
Modélisation de la vitesse de réaction.
6.1 Indiquer parmi les deux modèles suivants, celui qui modélise le mieux les résultats expérimentaux.
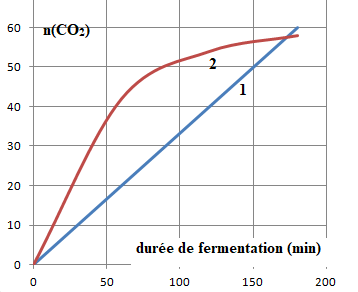
D'après le premier graphique, n(CO2) est une fonction linéaire du temps.
temps (heure)
|
1
|
2
|
3
|
n(CO2) mmol
|
18
|
36
|
55
|
Le modèle (2) est a rejeté.
6.2. La vitesse d'apparition de CO2 est-elle constante au cours du temps ?
Modèle 2.
La vitesse d'apparition du CO2 est égale au coefficient
directeur de la tangente à la courbe (2) à la date considérée. Or ces
tangentes sont de moins en moins inclinée sur l'horizontale. La vitesse d'apparition du CO2 diminue au cours du temps.
Modèle 1. La vitesse d'apparition du CO2 est constante au cours du temps.
6.3 Comment varie au cours du temps la vitesse d'apparition d'une espèce chimique qui suit une loi d'ordre de vitesse d'ordre 1 ?
v = d(nCO2) / dt = k n(CO2) avec k une constante.
La vitesse d'apparition de CO2 est une fonction linéaire de la quantité de matière de CO2.
6.4. Parmi les évolutions présentées à la question 6.1, laquelle peut modéliser une loi de vitesse d'ordre 1 ? Conclure.
Modèle 1.
La réaction de production du dioxyde de carbone dans la pâte suit une loi de vitesse d'ordre 1.
|
...
|
....
|
2. Acicification de la pâte et production de dioxyde de carbone.
Lors de la fermentation de la pâte, des mesures de pH ont montré une acidification, le pH évoluant de 6,0 à 4,8.
Hypothèse 1 :
L'acidification de la pâte est due uniquement à la production de CO2.
CO2, H2O aq + H2O = HCO3-aq + H3O+aq (2).
2.1
Donner l'expression reliant le pH et la concentration en ion oxonium
puis indiquer qualitativement pourquoi la production de dioxyde de
carbone peut être responsable de la baisse du pH.
pH = - log[H3O+aq].
D'après (2), la concentration en ion oxonium augmente et le pH diminue.
2.2. Donner à
l'équilibre la relation entre le quotient de réaction et la constante
d'équilibre. Ecrire l'expression de cette constante d'équilibre K.
A l'équilibre Ka = Q r éq = [ HCO3-aq]éq [H3O+aq ]éq / [CO2, H2O aq ] éq.
Pour évaluer l'influence de l'acide carbonique sur la diminution du pH,
on réalise une solution de volume V = 50 mL de concentration c = 7,0 10-6
mol / L en dioxyde de carbone solvaté apporté qui correspond à la
concentration en dioxyde de carbone dans la pâte en fin de levée. Le pH
de cette solution est pH = 5,8.
2.3. Justifier l'égalité des concentrations en H3O+aq et HCO3-aq à l'équilibre.
La solution est électriquement neutre et HO- aq est négligeable à pH = 5,8.
2.4. Déterminer [CO2, H2O aq ] éq.
pKa (CO2, H2O aq / HCO3-aq) = 6,37 ; Ka = 4,26 10-7.
[CO2, H2O aq ] éq =[H3O+aq ]2éq / Ka =(10-5,8)2 / (4,26 10-7) =5,9 10-6 mol / L.
La concentration en CO2 dissous a peu diminuée passant de 7,0 10-6 à 5,9 10-6 mol / L. L'acidification de la pâte n'est pas due uniquement à la production de CO2.
3. Rôle de l'acide succinique produit lors de la fermentation.
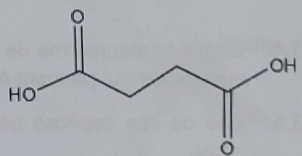
3.1 Représenter la formule semi-développée de cet acide et justifier le fait que c'est un diacide.
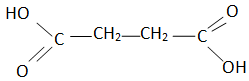
Cet acide possède deux groupes carboxyle ; il est susceptible de céder 2 protons.
3.2 Choisir parmi les propositions suivantes le nom de cet acide en nomenclature officielle.
éthanoate d'éthyle ; acide hexanoïque ; acide butanoïque ; acide éthanedioïque vrai.
3.3 Montrer que le spectre IR suivant peut être attribué à cet acide.
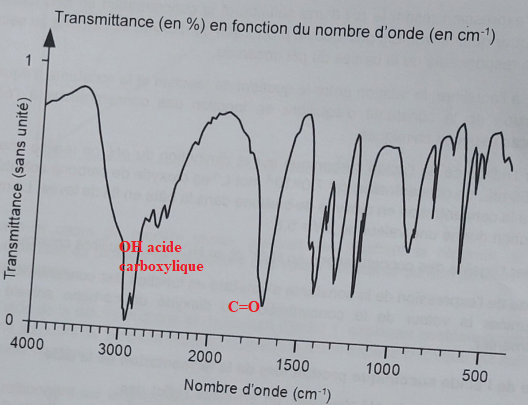
3.4 Etablir le
diagramme de prédominance des différentes espèces acide / base issues
de cet acide pouvant être présentes dans la pâte.
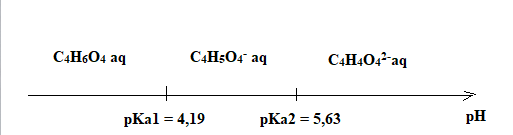
3.5 Identifier l'espèce amphotère.
C4H5O4- aq peut se comporter comme un acide ou comme une base.
On réalise 50 mL de solution de concentration 0,031 mol / L en accide
sussinique apporté ( concentration en fin de levée de la pâte ). On
mesure son pH : pH = 5,0.
3.6 Quelle masse d'acide succinique (M = 118 g / mol) solide faut-il prélever pour préparer cette solution.
n = 0,031 x 50 / 1000 =1,55 10-3 mol.
1,55 10-3 x 118 =0,18 g.
3.7. Ecrire le protocole succinct permettant de réaliser cette solution.
Peser à la balance de précision 0,18 g de solide ( balance tarée, spatule, coupelle).
Verser dans une fiole jaugée contenant 1 /3 d'eau distillée.
Agiter jusqu'à dissolution complète.
Ajouter de l'eau distillée jusqu'au trait de jauge.
Agiter pour rendre homogène.
3.8 Expliquer pourquoi l'hypothèse d'un lien entre acidification de la pâte et production d'acide succinique est plausible.
Le pH de la solution préparée est pH = 5,0.
Le pH de la âte après fermentation vaut 4,8.
|
|