Math�matiques, suites et fonctions, Bac centres �trangers 2022. Afrique du Sud, Bulgarie, Comores, Djibouti, Kenya, Liban, Lituanie, Madagascar, Mozambique et Ukraine En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicit�s adapt�es � vos centres d’int�r�ts. . . . . . . .. .. ...... ... 1. Soit f la fonction d�finie sur R par f (x) = x/ e x . On suppose que f est d�rivable sur R et on note f ′ sa fonction d�riv�e.  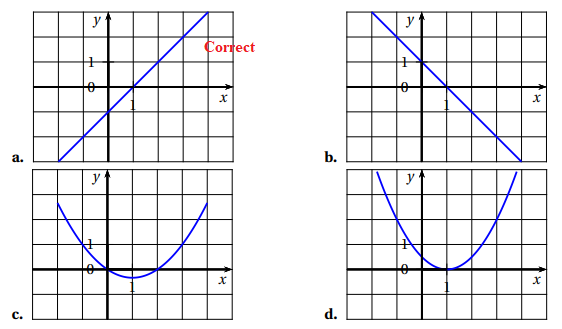a. f ′ (x) = e −x ; b. f ′ (x) = xe −x ; c. f ′ (x) = (1− x)e−x;  d. f ′ (x) = (1+ x)e−x . f(x) = x e-x. On d�rive en posant u = x, v = e-x ; u'=1 ; v' = -e-x. u'v+v'u = e-x-xe-x=e-x(1-x). 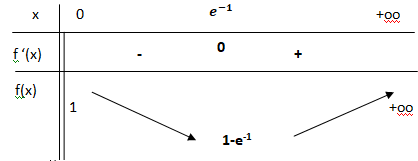2. Soit f une fonction deux fois d�rivable sur l’intervalle [−3 ; 1]. On donne ci-dessous la repr�sentation graphique de sa fonction d�riv�e seconde f ′′ . On peut alors affirmer que :  a. La fonction f est convexe sur l’intervalle [−1 ; 1]  ; b. La fonction f est concave sur l’intervalle [−2 ; 0]  ; c. La fonction f ′ est d�croissante sur l’intervalle [−2 ; 0] ; d. La fonction f ′ admet un maximum en x = −1. f " est positive sur [-3 ; -1], n�gative sur [-1 ; 1] s'annule pour x = -1. f ' est croissante sur [ -3 ; -1] et d�croissante sur [-1 ; 1 ] Donc f ' admet un maximum en x = -1. 3. On consid�re la fonction f d�finie sur R par : f (x) = x 3 exp( −x 2).  Si F est une primitive de f sur R, a. F(x) = − 1/ 6 ( x 3 +1) exp( −x 2).  b. F(x) = − 1 /4 x 4 exp( −x 2).  c. F(x) = − 1/2 ( x 2 +1 ) exp( −x 2) ;  d. F(x) = x 2 ( 3−2x 2 ) exp( −x 2). On d�rive − 1 /4 x 4 exp( −x 2). en posant :u = -0,25 x4 et v = exp( −x 2). u' = -x3 ; v' = -2x exp( −x 2) ; u'v+v'u = -x3 exp( −x 2)+0,5x5 exp( −x 2) ne convient pas. On d�rive   − 1/2 ( x 2 +1 ) exp( −x 2). en posant : u = − 0,5 ( x 2 +1 ) et v = exp( −x 2). u' = -x ; v' = -2x exp( −x 2) ; u'v+v'u = -x exp( −x 2)+x( x 2 +1 ) exp( −x 2)= x 3 exp( −x 2). 4. Que vaut la limite en plus l'infini de (ex+1) / (ex-1) ?  a. −1 ; b. 1 ; c. +∞;  d. n’existe pas. On met ex en facteur commun : ex(1+e-x) / [ex(1-e-x)] =(1+e-x) /(1-e-x). e-x tend vers z�ro si x tend vers plue l'infini et (ex+1) / (ex-1) tend vers 1.  5. On consid�re la fonction f d�finie sur R par f (x) = e 2x+1 . La seule primitive F sur R de la fonction f telle que F(0) = 1 est la fonction : a. F(x)= 2e2x+1 −2e+1 ; b.F(x)= 2e2x+1 −e ; c. F(x)= 0,5 e 2x+1 − 0,5 e+1  ; F(x)= exp(x2+x). On d�rive 2e2x+1 −2e+1 ; f(x) = 4e2x+1 ne convient pas. On d�rive 0,5e2x+1 −0,5e+1 ; f(x) = e2x+1  convient. 6. Dans un rep�re, on a trac� ci-contre la courbe repr�sentative d’une fonction f d�finie et deux fois d�rivable sur [−2 ; 4]. 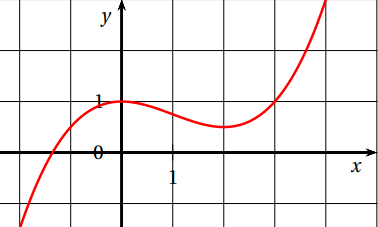Parmi les courbes suivantes, laquelle repr�sente la fonction f ′′, d�riv�e seconde de f ? f(x) est concave sur [-2 ; 1]  et convexe sur [1 ; 4]. f "(x) < 0 sur [-2 ; 1) et f "(x) > 0 sur [1 ; 4] s'annulant pour x = 1. ... .... Soit f la fonction d�finie sur l’intervalle ]0 ; +∞[ par f (x) = x ln(x)+1.  On note Cf sa courbe repr�sentative dans un rep�re du plan.  1. D�terminer la limite de la fonction f en 0 ainsi que sa limite en +∞. En z�ro : ln(x) tend vers moins l'infini ; x ln(x) tend vers z�ro et f(x) tend vers 1. En plus l'infini : ln(x) tend vers plus l'infini ; x ln(x) tend vers plus l'infini et f(x) tend vers plus l'infini.  2. a. On admet que f est d�rivable sur ]0 ; +∞[ et on notera f ′ sa fonction d�riv�e. Montrer que pour tout r�el x strictement positif : f ′ (x) = 1+ln(x). On pose u = x et v = ln(x) ; u' = 1 ; v' = 1 /x. u'v +v'u = ln(x) +1.  b. En d�duire le tableau de variation de la fonction f sur ]0 ; +∞[. On y fera figurer la valeur exacte de l’extremum de f sur ]0 ; +∞[ et les limites. f '(x) = 0 si ln(x) = -1 soit x = e-1. f '(x) >0 sur [e-1 ; +oo[ et f(x) croissante. f '(x) < 0 sur ]0 ; e-1 ] et f(x) d�croissante.  c. Justifier que pour tout x ∈]0 ; 1[, f (x) ∈]0 ; 1[. Sur ]0 ; e-1], f(x) d�cro�t 1 � 1-1/e ~0,63. Sur [e-1 ; 1[ cro�t de 1-1 /e � 1, valeur exclue. 3. a. D�terminer une �quation de la tangente (T ) � la courbe Cf au point d’abscisse 1. Coefficient directeur de T= f '(1) = 1. Le point de coordonn�es (1 ; f(1) =1 appartient � T. Equation de T : y = x+b ; 1 = 1+b ; b =0 ; y = x. b. �tudier la convexit� de la fonction f sur ]0 ; +∞[. f ''(x) = 1 /x avec x >0. f "(x) �tant positive , f(x) est convexe.  c. En d�duire que pour tout r�el x strictement positif : f (x) > x . La fonction �tant convexe, sa courbe repr�sentative est au dessus de toutes ses tangentes : donc f(x) > x. 4. On d�finit la suite (un) par son premier terme u0 �l�ment de l’intervalle ]0; 1[ et pour tout entier naturel n : un+1 = f (un).  a. D�montrer par r�currence que pour tout entier naturel n, on a : 0 < un < 1. Initialisation : 0 < u0 < 1 est vrai. H�r�dit� : 0 < un < 1. est suppos� vrai. D’apr�s la question 2.c, x ∈]0 ; 1[, f (x) ∈]0 ; 1[ , donc f (un) ∈]0 ; 1[ soit un+1 ∈]0 ; 1[. Conclusion : La propri�t� est vraie au rang 0 et h�r�ditaire. Elle est vraie, pour tout entier naturel n. b. D�duire de la question 3. c. la croissance de la suite (un). f (x) > x . et un >0, donc f(un) > un soit un+1 > un. La suite est croissante.  c. En d�duire que la suite (un) est convergente. La suite est croissante et major�e par 1, donc elle converge.

menu