Mathématiques, probabilités, Bac centres étrangers 2022. Afrique du Sud, Bulgarie, Comores, Djibouti, Kenya, Liban, Lituanie, Madagascar, Mozambique et Ukraine En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . . . .. .. ...... ... Dans une station de ski, il existe deux types de forfait selon l’âge du skieur : -un forfait JUNIOR pour les personnes de moins de 25 ans ; - un forfait SENIOR pour les autres.  Par ailleurs, un usager peut choisir, en plus du forfait correspondant à son âge l’option coupe-file qui permet d’écourter le temps d’attente aux remontées mécaniques. On admet que : - 20 % des skieurs ont un forfait JUNIOR ; - 80 % des skieurs ont un forfait SENIOR ; - parmi les skieurs ayant un forfait JUNIOR, 6 % choisissent l’option coupe-file ;  - parmi les skieurs ayant un forfait SENIOR, 12,5 % choisissent l’option coupe-file.  On interroge un skieur au hasard et on considère les évènements :  - J : « le skieur a un forfait JUNIOR »; - C : « le skieur choisit l’option coupe-file ». Les deux parties peuvent être traitées de manière indépendante Partie A 1. Traduire la situation par un arbre pondéré. 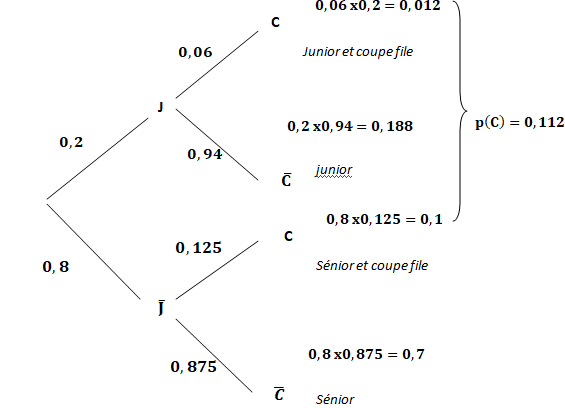2. Calculer la probabilité P(J ∩C). 0,06 x0,2 = 0,012. 3. Démontrer que la probabilité que le skieur choisisse l’option coupe-file est égale à 0,112. P(J n C) + P(non J n C) = 0,012 + 0,1 = 0,112.  4. Le skieur a choisi l’option coupe-file. Quelle est la probabilité qu’il s’agisse d’un skieur ayant un forfait SENIOR ? Arrondir le résultat à 10−3 . PC(non J) =P(non J n C) / P(C) = 0,1 / 0,112=0,893.  5. Est-il vrai que les personnes de moins de vingt-cinq ans représentent moins de 15 % des skieurs ayant choisi l’option coupe-file ? Expliquer. 1-0,893=0,107 soit 10,7 %. l'affirmation est fausse. Partie B On rappelle que la probabilité qu’un skieur choisisse l’option coupe-file est égale à 0,112. On considère un échantillon de 30 skieurs choisis au hasard. Soit X la variable aléatoire qui compte le nombre des skieurs de l’échantillon ayant choisi t’option coupe-file. 1. On admet que la variable aléatoire X suit une loi binomiale. Donner les paramètres de cette loi. n =30 ; p =0,112. 2. Calculer la probabilité qu’au moins un des 30 skieurs ait choisi l’option coupe-file. Arrondir le résultat à 10−3 . P(X > 1) = 1 -P(X=0)=1-(300) x 0,1120 x(1-0,112)30 =0,972.  3. Calculer la probabilité qu’au plus un des 30 skieurs ait choisi l’option coupe-file. Arrondir le résultat à 10−3 . P(X=0)+P(X=1)=(300) x 0,1120 x(1-0,112)30 +(301) x 0,1121 x(1-0,112)29 =0,136.  4. Calculer l’espérance mathématique de la variable aléatoire X.  E(X) = n p = 30 x0,112 =3,36. ... .... Une urne contient des jetons blancs et noirs tous indiscernables au toucher.  Une partie consiste à prélever au hasard successivement et avec remise deux jetons de cette urne. On établit la règle de jeu suivante :  - un joueur perd 9 euros si les deux jetons tirés sont de couleur blanche ; - un joueur perd 1 euro si les deux jetons tirés sont de couleur noire ;  - un joueur gagne 5 euros si les deux jetons tirés sont de couleurs différentes.  1. On considère que l’urne contient 2 jetons noirs et 3 jetons blancs.  a. Modéliser la situation à l’aide d’un arbre pondéré. On note B l'événement " le joueur tire un blanc". N l'événement " le joueur tire un noir".  b. Calculer la probabilité de perdre 9 € sur une partie. 2 jetons blancs sont tirés ; probabilité 0,36.  2. On considère maintenant que l’urne contient 3 jetons blancs et au moins deux jetons noirs mais on ne connait pas le nombre exact de jetons noirs. On appellera N le nombre de jetons noirs. a. Soit X la variable aléatoire donnant le gain du jeu pour une partie. Déterminer la loi de probabilité de cette variable aléatoire. Gain -9 -1 5 Probabilité (3 / (3+N)2 (N / (3+N)2 6N /(3+N)2.  b. Résoudre l’inéquation pour x réel : −x 2 +30x −81 > 0. Discriminant D =302-4*81=576=242. x1 = (-30 +24) /(-2) =3 ; x2 = (-30 -24) /(-2) =27. −x 2 +30x −81 > 0 si x appartient à ]3 ; 27[. c. En utilisant le résultat de la question précédente, déterminer le nombre de jetons noirs que l’urne doit contenir afin que ce jeu soit favorable au joueur. Espérence de X : E =( -9 *9-N2 +5(6N)2) / (3+N)2= (-N 2 +30N −81) / (3+N)2. Le jeu est favorable si l'espérance  est positive, soit N appartenant à ]3 ; 27[ . Donc entre 4 et 26 jetons noirs. d. Combien de jetons noirs le joueur doit-il demander afin d’obtenir un gain moyen maximal ? f (N) =(-N 2 +30N −81) / (3+N)2. On dérive en posant u = -N 2 +30N −81 et v= (3+N)2. u' = -2N+30 ; v' = 2(3+N) (u'v-v'u) / v2 =[(-2N+30)(3+N)2 -2(3+N)(-N2+30N-81)] / (3+N)4. Numérateur : (3+N) [-6N-2N2+90+30N+2N2-60N+162] =(3+N)(-36 N+252). f '(N) s'annule pour -66N = 252 soit N =7. Le gain moyen est maximum pour N=7 jetons noirs.  3. On observe 10 joueurs qui tentent leur chance en effectuant une partie de ce jeu, indépendamment les uns des autres. On suppose que 7 jetons noirs ont été placés dans l’urne (avec 3 jetons blancs). Quelle est la probabilité d’avoir au moins 1 joueur gagnant 5 euros ? Probabilité de gagner 5 € : (6 *7) / 102 =0,42. On note X le nombre de personnes gagnat 5 €. X suit une loi binomiale de paramètre n = 10 et p = 0,42. P(X >1) = 1-P(X=0)=1-(100) x 0,420 x(1-0,42)10=0,996.

menu