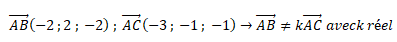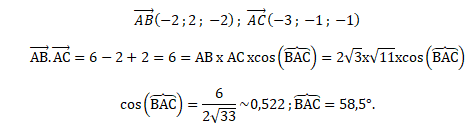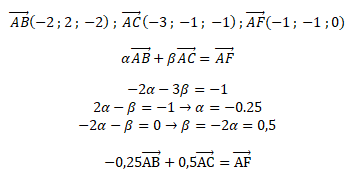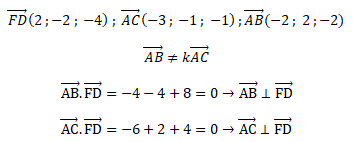Mathématiques,
géométrie, probabilités, Bac centres étrangers
2022.
Arabie saoudite, Bahreïn, Chypre, Éthiopie,
Grèce, Israël, Jordanie, Koweït, Qatar, Roumanie et Turquie
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
Dans
l’espace, rapporté à un repère orthonormé, on considère les points :
A(2 ; 0 ; 3), B(0 ; 2 ; 1),C(−1 ; −1 ; 2) et D(3 ; −3 ; −1).
1. Calcul d’un angle
a. Calculer les
coordonnées des vecteurs suivants et en déduire que les points A, B et
C ne
sont pas alignés.
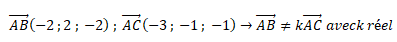
Donc les points A, B et C ne sont pas alignés.
b. Calculer les
longueurs AB et AC.
AB = [(-2) 2 +2 2+(-2) 2] ½ =12 ½
= 2 *3 ½.
AC = [(-3)2
+(-1)2+(-1)2]½ =11½.
c. À l’aide du produit
scalaire suivant, déterminer la valeur du cosinus de l’angle BAC puis �
donner une valeur approchée de la mesure de l’angle BAC au dixième de
degré.
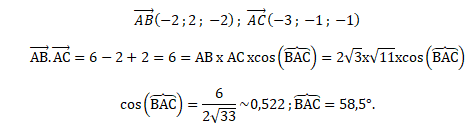 �
2. Calcul d’une aire
a.
�
2. Calcul d’une aire
a. Déterminer une
équation du plan P passant par le point C et perpendiculaire à la
droite
(AB).
Equation du plan : -2x+2y-2z +d = 0
C(-1 ; -1 ; 2) appartient à ce plan : 2-2-4+d=0 ; d = 4.
-2x+2y-2z +4 =
0 ou -x+y-z+2=0.
b. Donner une
représentation paramétrique de la droite (AB).
x = -2t +x A = -2t+2
y=2t+y A=2t.
z=-2t+z A =-2t+3 avec t réel.
c. En déduire
les coordonnées du projeté orthogonal E du point C sur la droite (AB),
c’est-àdire du point d’intersection de la droite (AB) et du plan P.
-x E+y E-z E+2 =0.
x E = -2t +2.
y E =2t.
z E = -2t+3.
2t-2 +2t+2+2t-3 =0 ; 6t -3=0 ; t =0,5.
xE
=1 ; yE =1 ; zE = 2.
d. Calculer l’aire
du triangle ABC.
CE x AB / 2.
CE =(2 2+2 2+0 2) ½ =8 ½
= 2 *2 ½.
AB = 2 *3½.
Aire : 2*6½.
3. Calcul
d’un volume
a. Soit le point
F(1 ; −1 ; 3). Montrer que les points A, B, C et F sont coplanaires.
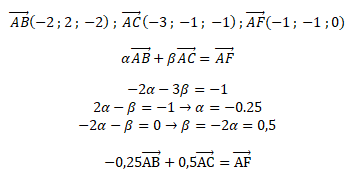 b.
b. Vérifier que la
droite (FD) est orthogonale au plan (ABC).
Coordonnées d'un vecteur directeur de la droite (FD) :( 2 ; -2 ; -4)
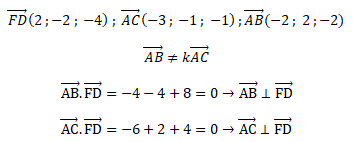 c.
c.
Sachant que le volume d’un tétraèdre est égal au tiers de l’aire de sa
base multiplié par sa
hauteur, calculer le volume du tétraèdre ABCD.
Hauteur FD =(2 2 +(-2) 2 +(-4) 2) ½
=24 ½=2*6 ½.
Base ABC : 2*6 ½.
V =24 /3 =8 untés de volume.
|
...
|
....
|
Probabilités.
Les parties A et B peuvent être traitées de façon indépendante.
Au cours de la fabrication d’une paire de lunettes, la paire de
verres doit subir deux traitements notés
T1 et T2.
Partie A
On prélève au hasard une paire de verres dans la production.
On désigne par A l’évènement : « la paire de verres présente un
défaut pour le traitement T1 ».
On désigne par B l’évènement : « la paire de verres présente un
défaut pour le traitement T2 ».
Une étude a montré que :
- la probabilité qu’une paire de verres présente un défaut pour le
traitement T1 notée P(A) est
égale à 0,1.
- la probabilité qu’une paire de verres présente un défaut pour le
traitement T2 notée P(B) est
égale à 0,2.
- la probabilité qu’une paire de verres ne présente aucun des deux
défauts est 0,75.
1. Recopier et
compléter le tableau suivant avec les probabilités correspondantes.
|
A
|
non
A
|
Total
|
B
|
0,05
|
0,15
|
0,2
|
non
B
|
0,05
|
0,75
|
0,8
|
Total
|
0,1
|
0,9
|
1
|
2. a. Déterminer,
en justifiant la réponse, la probabilité qu’une paire de verres,
prélevée au hasard dans la production, présente un défaut pour au moins
un des deux traitements T1 ou
T2.
C'est l"événement contraire de " aucun défaut " soit 1-0,75 = 0,25.
b. Donner la
probabilité qu’une paire de verres, prélevée au hasard dans la
production, présente deux défauts, un pour chaque traitement T1
et T2.
P(A n B) = 0,05.
c. Les évènements
A et B sont-ils indépendants ? Justifier la réponse.
P(A) x P(B) = 0,1 x 0,2 = 0,02 et P(A n B) =0,05.
Les événements ne sont pas indépendants.
3. Calculer la
probabilité qu’une paire de verres, prélevée au hasard dans la
production, présente
un défaut pour un seul des deux traitements.
P(A n non B) + P(B n non A) = 0,05 +0,15 = 0,2.
4. Calculer la
probabilité qu’une paire de verres, prélevée au hasard dans la
production, présente
un défaut pour le traitement T2, sachant que cette paire de
verres présente un défaut pour le
traitement T1.
PA(B) =P(A n B) / P(A) =0,05 / 0,1 = 0,5.
Partie B.
On prélève, au hasard, un échantillon de 50 paires de verres dans
la production. On suppose que la
production est suffisamment importante pour assimiler ce prélèvement à
un tirage avec remise.
On note X la variable aléatoire qui, à chaque échantillon de ce type,
associe le nombre de paires de
verres qui présentent le défaut pour le traitement T1.
1. Justifier que la
variable aléatoire X suit une loi binomiale et préciser les paramètres
de cette loi.
Les tirages sont indépendants ; chaque tirage est une épreuve de Bernoulli.
X suit la loi binomiale de paramètre n = 50 et p = 0,1.
2. Donner
l’expression permettant de calculer la probabilité d’avoir, dans un tel
échantillon, exactement 10 paires de verres qui présentent ce défaut.
Effectuer ce calcul et arrondir le résultat à 10−3
.
P(X = 10) = (5010) x0,110 x 0,940 ~0,015.
3. En moyenne,
combien de paires de verres ayant ce défaut peut-on trouver dans un
échantillon
de 50 paires ?
Espérance de X = np = 50 x0,1 = 5.
|
|