Mise
à température d'une lunette
astronomique, observation de mars, bac centre étranger 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
|
.
.
|
..
..
......
...
|
A.
Distance maximale terre-mars permettant d'observer la calotte polaire
Nord
La lunette est afocale. Elle est modélisée par deux lentilles
convergentes L1 et L2.
On cherche à former l'image d'un objet situé à l'infini.
1. Donner le nom
des deux lentilles.
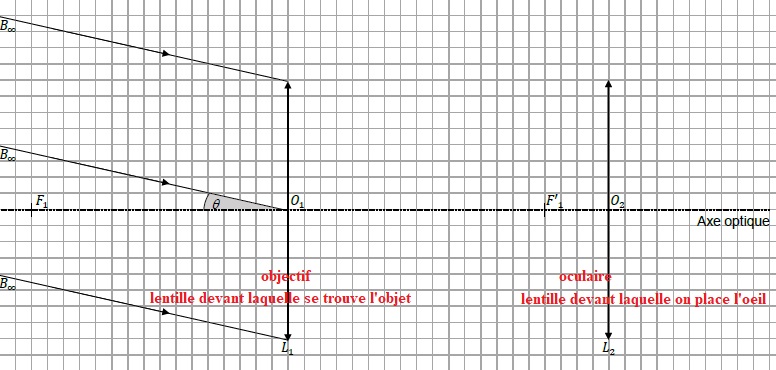
2. Représenter le faisceau issus du
point Aoo délimité par les rayons 1 et 2 et émergent de la
lunette. .
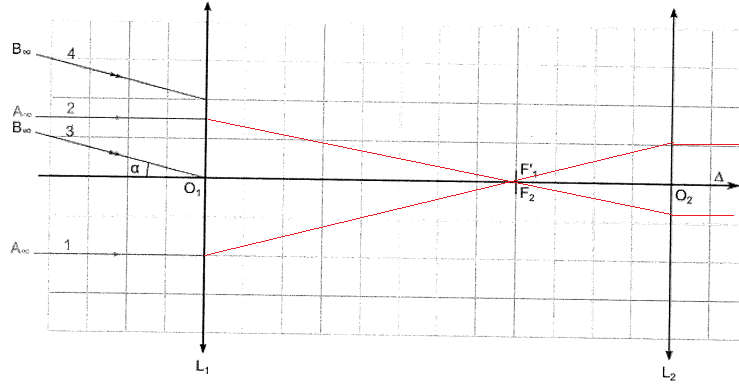
3. Représenter le
faisceau issus du point Boo délimité par les rayons 3 et 4 et émergent de
la lunette.
4.
Faire apparaître l'angle a'
sous lequel est vue l'image de l'objet à l'infini à travers la lunette
ainsi que l'image intermédaire A1B1.
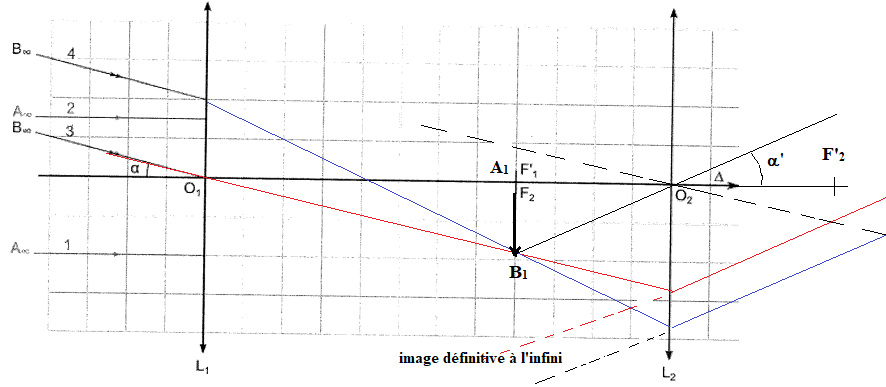
5. Justifier le terme "afocal".
Des rayons parallèles entre eux avant le
système optique, ressortent parallèles après le système.
Visibilité de la calotte
polaire.
6. Rappeler la
définition du grossissement G.
G =a' / a.
7. Montrer que le
grossissement peut se mettre sous la forme G = f '1 / f '2.
Triangle O1A1B1 : tan a ~a = A1B1
/ O1F'1= A1B1
/ f '1.
Triangle O2A1B1
: tan a' ~a' = A1B1
/ O2F2= A1B1 / f '2.
Par suite : G = f '1
/ f '2.
On note amini
la valeur minimale de a
pour que l'objet soit observable par un l'oeil à l'aide de cette
lunette.
8. Exprimer amini en fonction de f '1, f '2
et q0.=2,7
10-4 rad, pouvoir séparateur de l'oeil. Vérifier que amini =5,9 10-6 rad.
f '1 = 0,91 m
; f '2 = 0,020 m.
G =
q0 / amini
=f '1 / f '2.
c = A / 0,0875 =0,484 /
0,0875 =5,53 µmol / L.
amini= q0 f '2 / f '1 =2,7 10-4
x0,020 / 0,91 =5,9 10-6
rad.
9. La taille de la calotte polaire
Nord de Mars a un diamètre d~103 km, donner un estimation,
en km, de la distance maximale D entre Mars et la Terre permettant
d'observer cette calottte.
amini=
d / D ; D = d / amini= 103
/(5,9 10-6) ~1,7 108 km.
La distance Terre-Mars varie entre 0,5 et 2,5 ua.
10. L'astronome
pourra t-il observer cette calotte avec sa lunette.
1 ua = 1,5 1011m = 1,5 108 km.
Distance minimale Terre-Mars : 0,5 x1,5 108 =7,5 107
km.
Distance
maximale Terre-Mars : 2,5 x1,5 108 =3,75 108 km.
D étant comprise entre ces deux valeurs, la calotte est observable.
|
...
|
....
|
B. Mise en température avant observation.
La température de l'instrument ne doit pas s'écarter de la température
de l'air extérieur de plus de 1°C.
L'astronome cherche à savoir si une durée de 2 heurs pour la mise en
température de son instrument est suffisante pour limiter la turbulence
instrumentale. A t = 0, il met la lunette en contact avec l'air
extérieur et mesure sa température pendant 20 minutes à intervalles de
temps régulier.
Puis il utilise une modélisation théorique pour prédire l'évolution de
la température sur des durées plus longues.
q0 = 19,5 °C,
température initiale de la lunette ; qe = 9,0°C,
température de l'air extérieur.
11.
Indiquer le sens du transfert thermique au cours du refroidissement de
la lunette.
Transfert du corps chaud, la lunette, vers le corps froid, l'air
extérieur.
12. Enoncer le
premier principe de la thermodynalique.
DU = W
+ Q.
Dans ce cas le travail W est nul.
13. Montrer que la
varaition de température Dq
de la lunette sur une petite durée Dt vérifie :
C Dq = h S ( qe-q) Dt (1):
C : capacité thermique de la lunette.
Flux thermique F
= hS( qe-q) = Q / Dt.
h : coefficient d'échange thermique ; S aire de la surface d'échange.
DU =C Dq .
DU / Dt =C Dq / Dt =hS( qe-q).
C Dq = h S ( qe-q) Dt
14. En déduire que
la température de la lunette suit l'équation différentielle
dq(t) /dt +q(t) / t = qe / t (2).
On pose t = C /
(hS ) exprimé en seconde.
C Dq / Dt= h S ( qe-q).
Dq / Dt= h S / C ( qe-q).
Dq / Dt = qe/ t -q / t.
Dq / Dt + q / t = qe/ t .
La solution de cette équation est de la forme : q(t) =A exp(-t /t) +B avec A et B des
constantes.
16. Quelle est la
température finale de la lunette ?
qe
= 9°C.
17. Exprimer A en
fonction de q0
et qe..
q(t=0)
=A exp(0) +B = A + B = q0.
Au bout d'un temps suffisamment long la lunette se trouve à la
température qe.
qe=
B = 9
Par suite A = q0
-qe =
10,5. .
Simulation. t = 1414 s.
Sur le graphique suivant, les points expérimentaux sont représentés par
des + et le modèle théorique par la courbe en trait plein.
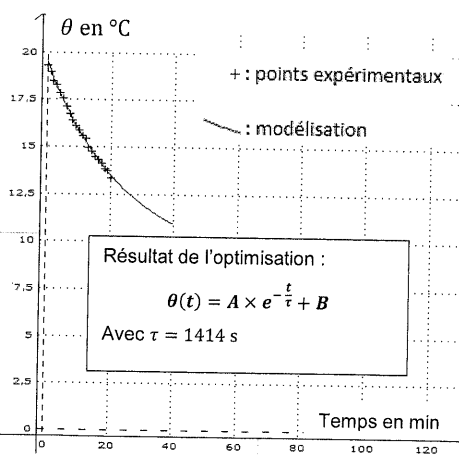
17. Discuter
qualitativement l'accord du modèle théorique avec les résultats
expérimentaux.
Les points expérimentaux coîncident avec le modèle théorique ; ce
dernier est en accord avec les expériences.
18. Vérifier que la
lunette peut être à température à t = 2 heures.
q(t =
7200 s) =10,5 exp(-7200 / 1414) +9 =6,4 10-2 +9 ~ 9 °C.
|
|