Mathématiques,
fonction logarithme, bac Nlle Calédonie 2022.
En
poursuivant votre navigation sur ce site, vous acceptez l’utilisation
de Cookies vous proposant des publicités adaptées à vos centres
d’intérêts.
.
| . |
.
.
|
|
.
.
|
..
..
......
...
|
On considère la fonction f
définie sur l’intervalle ]0 ; +∞[ par
f (x) = x2−6x +4ln(x).
On admet que la fonction f est deux fois dérivable sur l’intervalle ]0
; +∞[.
On note f ’ sa dérivée et f ′′ sa dérivée seconde.
On note Cf la courbe représentative de la fonction f dans un
repère orthogonal.
1. a. Déterminer la
limite de f quand x tend vers zéro. Interpréter graphiquement ce
résultat.
x2-6x tend vers zéro ; ln(x) tend vers moins l'infini ;
par somme des limites, f(x) tend vers moins l'infini.
L'axe des ordonnées est asymptote à la courbe Cf.
b. Déterminer lla
limite de f quand x tend vers plus l'infini.
f(x) = x[x-6+4ln(x) / x].
Par croissance comparée ln(x) / x tend vers zéro ; x-6+4ln(x) / x tend vers
plus l'infini.
Par produit des limites, f(x) tend vers plus l'infini.
2. a. Déterminer f
′(x) pour tout réel x appartenant à ]0 ; +∞[.
f '(x) = 2x-6+4 / x.
b. Étudier le signe
de f ′(x) sur l’intervalle ]0 ; +∞[. En déduire le tableau de
variations de f .
f '(x)= (2x2-6x+4) / x.
f '(x) a le signe de 2x2-6x+4 ;
2x2-6x+4
= 0 ; discriminant D
=62-4*4*2=4= 22.
Racines : x = (6 ±2)/ 4soit x1 =2 et x2 = 1.
Si x appartient à ]1 ; 2 [, f '(x) est négative et f(x) est strictement
décroissante.
S x appartient à ]0 ; 1[ union ]2 ; +oo[, f '(x) > 0 et f(x) est
strictement croissante.
si x = 1, f '(x) = 0
et f(x) présente un maximum.
si x = 2, f '(x) = 0
et f(x) présente un minimum.
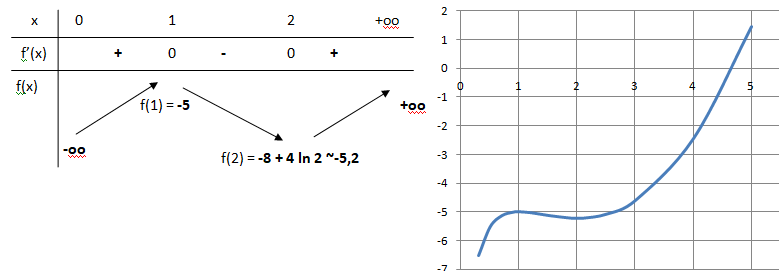
3. Montrer que
l’équation f (x) = 0 admet une unique solution dans l’intervalle [4; 5].
Sur cet intervalle, f(x) est continue car dérivable et strictement
croissante de -8 + 4 ln 4 ~ -2,45 à -5 +4ln 5 ~1,44.
D'après le théorème des valeurs intermédiaires, il existe un seul réel a de l'intervalle [4 ; 5]
tel que f(a) = 0.
4. On admet que,
pour tout x de ]0 ; +∞[, on a :
f "(x) =(2x2-4) / x2.
a. Étudier la
convexité de la fonction f sur ]0 ; +∞[.
On précisera les valeurs exactes des coordonnées des éventuels points
d’inflexion de Cf.
f "(x) > 0 si x > 2½ et f(x) est
convexe sur ]2½ ; +oo[.
f "(x)
< 0 si x < 2½ et f(x) est
concave sur ]0 ; 2½ [.
f "(x) s'annule et change de
signe pour 2x2-4
=0 soit x = 2½.
Le point de coordonnées 2½ et f(2½ ) =2-6*2½
+4 ln(2½) ~ -5,1 est un point d'inflexion.
b. On note A le point de
coordonnées(2½ ; f(2½).
Soit t un réel strictement positif tel que t diffère de 2½.
Soit M le point de coordonnées (t ; f (t )).
En utilisant la question 4. a, indiquer, selon la valeur de t , les
positions relatives du segment [AM] et de la courbe Cf
Si k appartient à ]0 ; 2½
[, AMk est une corde à la courbe d'une fonction concave : AMk
est en dessous de Cf.
Si k appartient à ] 2½ ; +oo[, AMk
est une corde à la courbe d'une fonction convexe : AMk est
au dessus de Cf.
|
...
|
....
|
Soit f la fonction définie sur l’intervalle ]0 ; +∞[ par :
f (x) = x ln(x)−x −2.
On admet que la fonction f est deux fois dérivable sur ]0 ; +∞[.
On note f œ' sa dérivée, f "œœ sa dérivée seconde et Cf sa courbe représentative dans un repère.
1. a. Démontrer que, pour tout x appartenant à ]0 ; +∞[, on a f '(x) = ln(x).
Dérivée de x ln(x) : on pose u = x et v = ln(x) ; u' = 1 ; v' = 1 /x.
u'v+v'u = ln(x)+1.
f '(x) = ln(x) +1 -1 = ln(x).
b. Déterminer une équation de la tangente T à la courbe Cf au point d’abscisse x =e.
Coefficient directeur de T : f '(e) = ln(e) = 1.
Equation de T : y = x+b.
Le point de coordonées ( e ; f(e) =-2) appartient à la tangente.
-2 = e+b ; b = -2-e.
y = x -2-e.
c. Justifier que la fonction f est convexe sur l’intervalle ]0 ; +∞[.
f "(x) =1 /x.
f "(x) >0 sur ]0 ; +oo[, donc f est convexe sur cet intervalle.
d. En déduire la position relative de la courbe Cf et de la tangente T.
La fonction étant convexe, la courbe Cf est au dessus de la tangente T.
2. a. Calculer la limite de la fonction f en 0.
-x-2 tend vers -2 ;
ln(x) tend vers -oo ; par produit des limites x ln(x) tend vers zéro.
f(x) tend vers -2.
b. Démontrer que la limite de la fonction f en +∞est égale à +∞.
f(x) = x(ln(x) -1-2 /x).
-2 /x tend vers zéro ;
ln(x) tend vers +oo ; ln(x) -1 tend vers plus l'infini ;
par produit des limites x ln(x) tend vers +oo.
f(x) tend vers +oo.
3. Dresser le tableau de variations de la fonction f sur l’intervalle ]0 ; +∞[.
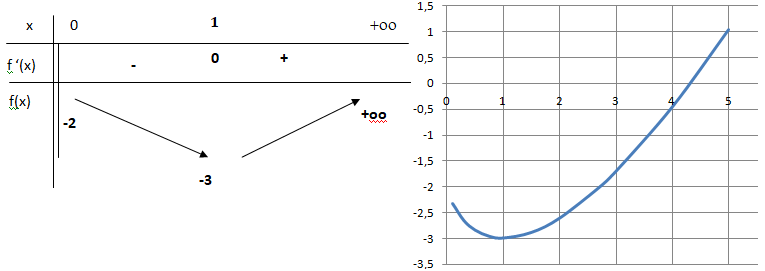
4. a. Démontrer que l’équation f (x) = 0 admet une unique solution dans l’intervalle ]0 ; +∞[. On note a cette solution.
Sur l'intervalle ]1 ; +∞[, f(x) est continue car dérivable et strictement
croissante de -3 à +oo.
D'après le théorème des valeurs intermédiaires, il existe un seul réel a de l'intervalle ]0 ; +∞[
tel que f(a) = 0.
b. Justifier que le réel a appartient à l’intervalle ]4,3; 4,4[.
f(4,3) =4,3 ln(4,3) -4,3 -2 ~ -0,027.
f(4,4) =4,4 ln(4,4) -4,4 -2 ~ 0,119.
D'après le théorème des valeurs intermédiaires, a appartient à l'intervalle ]04,3 ; 4,4[ .
c. En déduire le signe de la fonction f sur l’intervalle ]0 ; +∞[.
Si x < a, f(x) < 0 ; Si x > a, f(x) > 0 ; si x < a, f(x) < 0 ; si x = a, f(x) = 0.
5. On considère la fonction seuil suivante écrite dans le langage Python :
On rappelle que la fonction log du module math (que l’on suppose importé) désigne la fonction logarithme népérien ln.
def seuil(pas) :
x=4.3
while x*log (x) - x - 2 < 0:
x=x+pas
return x
Quelle est la valeur renvoyée à l’appel de la fonction seuil(0.01)?
Interpréter ce résultat dans le contexte de l’exercice.
La fonction seuil(0,01) renvoie 4,32.
On trouve l'encadrement de a au centième : 4,32 < a < 4,33.
|
|