Ingenuity, le premier hélicoptère à voler sur Mars, Bac Nlle Calédonie 2022.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . .

.
.
.. ..
......


...
A l'atmosphère de Mars.
La densité de l'atmosphère de Mars est 100 fois plus faible que sur la Terre.
A1. En supposant que l'air est un gaz parfait, montrer que la masse volumique de l'air sur Terre vérifie la relation :
rTerre = PM / (RT).
PV = n RT.
n = masse / masse molaire de l'air = m / M.
masse volumique = masse  / volume = m / V.
PV = m / M RT ; m / V = MP / (RT)
rTerre (kg m-3) ; M = 29,0 10-3 kg / mol ; T (K) ; R = 8,314 J mol-1 K-1 ; P=1,013 105 Pa.
A2. Calculer sa valeur pour une température de 15°C
rTerre =1,013 105 x29,0 10-3 / (8,314 x 288)=1,227 kg m-3.
La masse volumique de l'atmosphère de Mars est égale à 1 % de celle de la Terre.
 A3. En déduire la lasse volumique de l'atmosphère de Mars à la température de 15°C.
rMars =1,227 10-2 kg m-3.
A4. La portance est proportionnelle à la masse volumique de l'atmosphère dans laquelle se trouve l'engin; expliquer pourquoi c'est un défi technologique de faire voler un hélicoptère sur Mars.
Pour voler les pâles en rotation de l'hélicoptère génèrent une force verticale ascendante appelée " portance".
Sur Mars cette force  est 100 fois plus faible que sur Terre.

B. La phase de décollage.
Pour décoller la portance doit au moins compenser le poids de l'hélicoptère.
Masse de l'hélicoptère M =1,8 kg.
Intensité de la pesanteur sur Mars gM = 3,7 m s-2 ; sur Terre gT = 9,8 m s-2.
Poids de l'hélicoptère sur Mars PM = 1,8 x3,7 =3,66 N ; sur Terre PT = 1,8 x9,8 =17,6 N.
Les figures suivantes représentent l'évolution de la portance en fonction de la vitesse de rotation des pâles.
B1. Déterminer la valeur de la vitesse de rotation minimale des pâles afin que l'hélicoptère décolle.


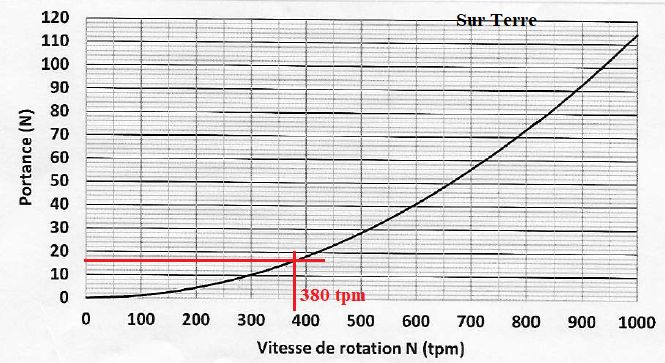
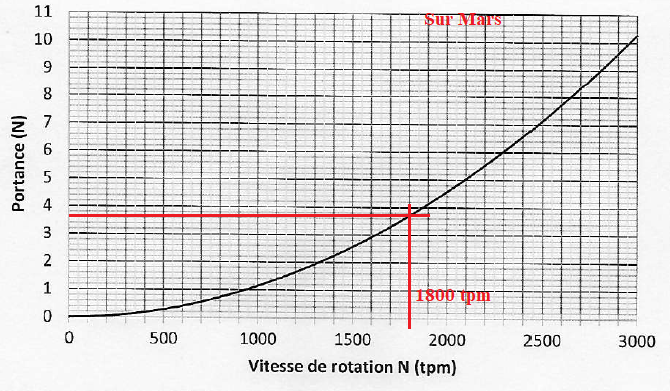
Sur Mars la vitesse minimale de rotation des pâles doit être près de 5 fois plus grande que sur Terre pour assurer un décollage.

...
....

 Partie C. Une phase d'atterrisage délicate.
La solution retenue est d'arrêter la propulsion à un mètre au dessus du sol et de laisser l'hélicoptère atteindre le sol en chute libre.
On suppose que la vitesse de l'hélicoptère est nulle à H = 1,0 m au dessus du sol. Il chute verticalement.


C1. Appliquer la seconde loi de Newton afin d'exprimer les coordonnées du vecteur accélération.
L'hélicoptère n'est soumis qu'à son poids P = mgM.
Coordonnées du vecteur accélération ( 0 ; -gM).
C2. En déduire la coordonnée vz(t) du vecteur vitesse.
vz(t) = -gMt = -3,7 t.
 C3. En déduire l'équation horaire z(t).
z(t) = -½gMt2 + H = -1,85 t2 + 1.
 C4. Déterminer la durée de la chute.
-1,85 t2 + 1,0 = 0 ; t = (1 / 1,85)½~ 0,735 ~0,74 s.
C5. Déterminer la vitesse au moment de l'impact sur le sol.
|v| = 3,7 t = 3,7 x 0,735 ~ 2,7 m /s. ( 9,8 m /s).
Le train d'atterrissage étant conçu pour résister à des vitesses de 16 km / h, ce trai n'est pas abimé.

D. Mesure de l'altitude au cours du vol.
Un groupe d'élèves réalise un altimètre pour un drône à l'aide d'un condensateur de capacité C variable en fonction de l'altitude z.
Le condensateur est placé dans le circuit ci-dessous. L'interrupteur est d'abord en position 1 : le condensateur se charge sous la tension E.
Puis l'interrupteur bascule en position 2 : le condensateur se décharge dans la résistance R = 1,0 kW.
Le drône se trouve dans un premier temps au niveau du sol.


D1. Au cours de la décharge; montrer que l'équation différentielle qui régit la tension aux bornes du condensateur s'écrit : duC /dt +uC /(RC) = 0.
uR + uC = 0.
uR = R i avec i = dq/dt = CduC /dt.
Par suite : duC /dt +uC /(RC) = 0.
D2. Montrer que la solution de cette équation s'écrit : uC(t) = E exp(-t / t) avec t = RC.
uC(t) = A E exp(-t / t) avec A une constante.
A t = 0, uC = E.
Par suite : uC(t) = E exp(-t / t).
D3. Déterminer graphiquement E et t.

D4. En déduire que Csol = C0 = 100 µF.
0,1 = 1,0 103 C0 ; C0 = 10-4 F = 100 µF.
Lorsque le drône monte, la pression atmosphérique diminue et provoque une augmentation de l'épaisseur e entre les armatures.

D5. Comment évolue la capacité du condensateur lorsque le drône s'éloigne du sol. La surfaces des armatures est constante.
C = e S /e.
Si e augmente avec eS constant, la capacité diminue.
D6. Estimer C à 5 m du sol sachant que la variation de pression provoque une augmentation d'épaisseur e de 10 %.
C0 =  eS / e ; C = eS / (1,1 e) = C0 / 1,1 = 100 / 1,1 ~91 µF.

  
menu